ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ 9 класс 1

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ 9 класс 1

2

РЕБУС «СОБЫТИЕ» 3

СОБЫТИЕ Под СОБЫТИЕМ понимается явление, которое происходит в результате осуществления какого-либо определенного комплекса условий. ПРИМЕР. Бросаем шестигранный игральный кубик. Определим события: А {выпало четное число очков}; В {выпало число очков, кратное 3}; С {выпало более 4 очков}. 4

ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами или явлениями в строго определенных условиях и измерении значений заранее определенных признаков этих объектов (явлений). • сдача экзамена, • наблюдение за дорожнотранспортными происшествиями, • выстрел из винтовки, • бросание игрального кубика, • химический эксперимент, • и т. п. 5

СЛУЧАЙНОЕ СОБЫТИЕ СЛУЧАЙНЫМ называют событие, которое может произойти или не произойти в результате некоторого испытания (опыта). Обозначают заглавными буквами А, В, С, Д, … (латинского алфавита). 6

Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов 7

Опыт 1: Подбрасывание монеты. Испытание – подбрасывание монеты; события – монета упала «орлом» или «решкой» . «решка» - лицевая сторона монеты (аверс) «орел» - обратная сторона монеты (реверс) 8

Опыт 2: Подбрасывание кубика. Это следующий по популярности после монеты случайный эксперимент. Испытание – подбрасывание кубика; события – выпало 1, 2, 3, 4, 5 или 6 очков (и другие). 9

Опыт 3: Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки. Опыт 4: «Завтра днем – ясная погода» . Здесь наступление дня – испытание, ясная погода – событие. 10

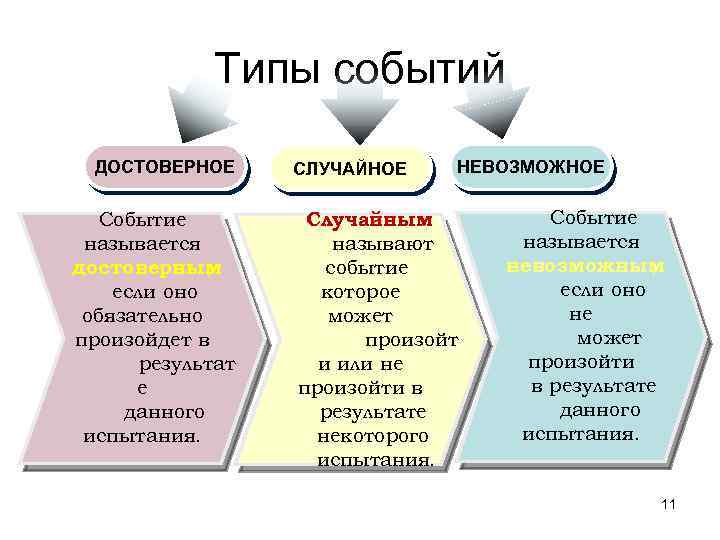Типы событий ДОСТОВЕРНОЕ Событие называется достоверным , если оно обязательно произойдет в результат е данного испытания. СЛУЧАЙНОЕ НЕВОЗМОЖНОЕ Случайным называют событие которое может произойт и или не произойти в результате некоторого испытания. Событие называется невозможным , если оно не может произойти в результате данного испытания. 11

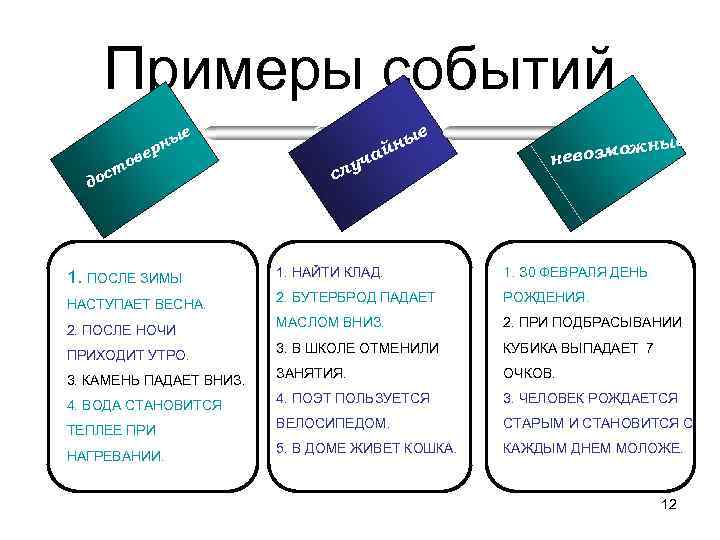Примеры событий е ны р ве о ст до 1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА. 2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО. 3. КАМЕНЬ ПАДАЕТ ВНИЗ. 4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ. е ы йн а уч сл ые жн евозмо н 1. НАЙТИ КЛАД. 1. З 0 ФЕВРАЛЯ ДЕНЬ 2. БУТЕРБРОД ПАДАЕТ РОЖДЕНИЯ. МАСЛОМ ВНИЗ. 2. ПРИ ПОДБРАСЫВАНИИ 3. В ШКОЛЕ ОТМЕНИЛИ КУБИКА ВЫПАДАЕТ 7 ЗАНЯТИЯ. ОЧКОВ. 4. ПОЭТ ПОЛЬЗУЕТСЯ 3. ЧЕЛОВЕК РОЖДАЕТСЯ ВЕЛОСИПЕДОМ. СТАРЫМ И СТАНОВИТСЯ С 5. В ДОМЕ ЖИВЕТ КОШКА. КАЖДЫМ ДНЕМ МОЛОЖЕ. 12

РЕБУС ИСХОДОМ (или элементарным исходом, элементарным событием) называется один из взаимоисключающих друга вариантов, которым может завершиться случайный эксперимент. 13

Число возможных исходов в каждом из рассмотренных выше опытах. Опыт 1. – 2 исхода: «орел» , «решка» . Опыт 2. – 6 исходов: 1, 2, 3, 4, 5, 6. Опыт 3. – 3 исхода: «обе перчатки на левую руку» , «обе перчатки на правую руку» , «перчатки на разные руки» . 14

Типы событий q Противоположное событие – В (по отношению к рассматриваемому событию А) – это событие , которое не происходит, если А происходит, и наоборот. q Например, событие А – «выпало четное число очков» и – В «выпало нечетное число очков» при бросании игрального кубика. События А и В– противоположные. 15

Случайные события Два события А и называются противоположными, если не появление одного из них в результате испытания влечет появление другого( отрицание А). События называются равновозможными , если по условию испытания нет оснований считать какоелибо из них более возможным, чем любое другое ( А-орел; В-решка). 16

Задание 1 Назовите событие противоположное данному: 1. При бросании монеты выпала решка; 2. Алеша вытащил выигрышный билет в розыгрыше лотереи; 3. В нашем классе все умные и красивые; 4. Мою соседку по парте зовут или Таня, или Аня; 5. Явка на выборы была от 40% до 47%; 6. Сегодня хорошая погода. 17

Типы событий q Два события А и В называют совместными , если они могут произойти одновременно при одном исходе эксперимента, и несовместными , если они не могут произойти одновременно ни при одном исходе эксперимента. Пример1. А – «идет дождь» , В – «на небе нет ни облачка» – несовместные. Пример 2. Коля и Саша играют в шашки. А – «Коля проиграл» , В – «Саша выиграл» , С – «Витя наблюдал за игрой» – совместные. 18

Примеры совместных и несовместных событий: совместные события: • идет дождь и идет снег, • человек ест и человек читает, • число целое и четное; несовместные события: • день и ночь, • человек читает и человек спит, • число иррациональное и четное. 19

Задание 2 Укажите совместность – несовместность случайных событий: а) (Катя с Ваней играли в шахматы) А – «Катя выиграла» , В – «Ваня проиграл» ; б) (Катя с Ваней играли в шахматы) А – «Катя проиграла» , В – «Ваня проиграл» ; в) (бросили кубик) А – «выпала шестерка» , В – «выпала пятерка» ; г) (бросили кубик) А – «выпала шестерка» , В – «выпало четное число очков» ; д) (взяли кость домино) А – «одно число 2» , В – «сумма обоих чисел 9» ; е) (взяли кость домино) А – «оба числа больше трех» , В – «сумма чисел 8» ; ж) А – «квадратное уравнение имеет два корня» , В – «дискриминант больше нуля» ; з) А – «квадратное уравнение не имеет действительных корней» , В – «дискриминант равен нулю» . 20

Действия над событиями 1. Суммойнескольких событий называется событие, состоящие в наступлении хотя бы одного из них в результате испытания. ( , ) Если события А и В совместныто сумма А+В , означает, что наступает событие А, или событие В, или оба события вместе. Если события несовместныто событие А+В , заключается в том, что должны наступить А или В, тогда + заменяется словом «или» . . 21

Действия над событиями Пример. В урне находятся красные, белые и черные шары. Вынимается один шар. Возможные события: v А – «вынут красный шар» , v В – «вынут белый шар» , v С – « вынут черный шар» . Тогда А+В означает, что произошло событие «вынут не черный шар» , В+С – «вынут не красный шар» . 22

Примерысуммы событий: • пусть А - идет дождь, а В - идет снег, • то (А + В) – либо дождь, либо снег, либо дождь со снегом, т. е. осадки; • А - пошли на дискотеку; В - пошли в библиотеку, • то А + В – пошли либо на дискотеку, либо в библиотеку, т. е. вышли из дома. 23

Действия над событиями 2. Произведением нескольких событий называется событие, состоящие в совместном наступлении всех этих событий в результате испытания( ). (АВС, это означает, что наступило событие и А и и С). Пример. Пусть имеются следующие события: А – «из колоды карт вынута дама» , В – «из колоды карт вынута карта пиковой масти» . Значит, А*В означает: «вынута дама пик» . Пример. Бросается игральный кубик. Рассмотрим следующие события: А – « число выпавших очков < 5» , В – «число выпавших очков > 2» , С – «число выпавших очков четное» . Тогда А*В*С – «выпало 4 очка» . 24

Примеры произведения событий: • пусть А - из урны вытянули белый шар, В - из урны вытянули белый шар, то А В –из урны вытянули два белых шара; • А - идет дождь, В - идет снег, то А В – • дождь со снегом; • А - число четное, В - число кратное 3, то А В – число кратное 6. 25