2_Множества.ppt
- Количество слайдов: 10

Основные понятия теории множеств Сентябрь, 200 6 Историческая справка n n n n Немецкий ученый, математик, создатель теории множеств Родился в Петербурге в 1845 г. В 1867 г. окончил Берлинский университет В 1872 -1913 гг. – профессор университета в Галле Сформулировал общее понятие мощности множества (1878) Развил принципы сравнения мощностей множеств Систематически изложил принципы своего учения Созданная Кантором теория множеств, некоторые идеи которой имелись у его предшественников, послужила причиной общего пересмотра логических основ математики и оказала влияние на всю современную ее структуру ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua Георг Кантор (XIX-XXвв. ) 1

Основные понятия теории множеств Сентябрь, 200 6 Понятие множества Мн ож ест о n n n в • Множество есть многое, мыслимое как единое Г. Кантор чка То Информация Множество является первичным понятием Множество рассматривается как совокупность объектов той или иной природы Объекты, которые образуют множество, называются его элементами ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 2
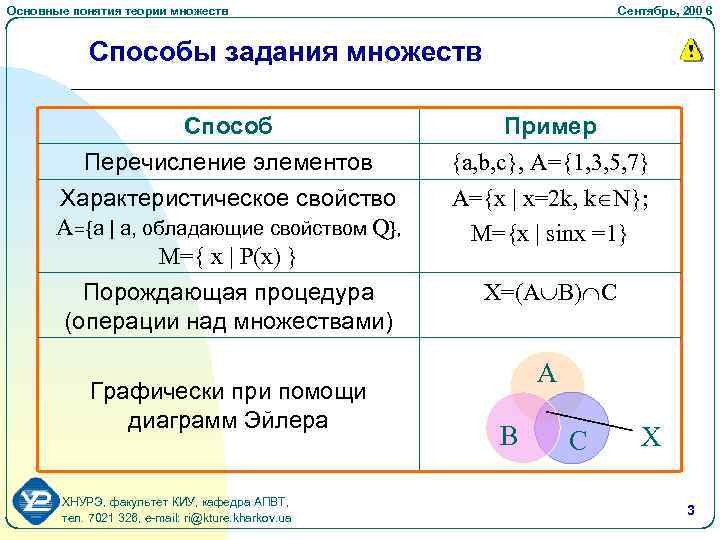
Основные понятия теории множеств Сентябрь, 200 6 Способы задания множеств Способ Перечисление элементов Характеристическое свойство A={a | a, обладающие свойством Q}, M={ x | P(x) } Пример {a, b, c}, A={1, 3, 5, 7} A={x | x=2 k, k N}; M={x | sinx =1} Порождающая процедура (операции над множествами) X=(A B) C Графически при помощи диаграмм Эйлера ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua A B C Х 3
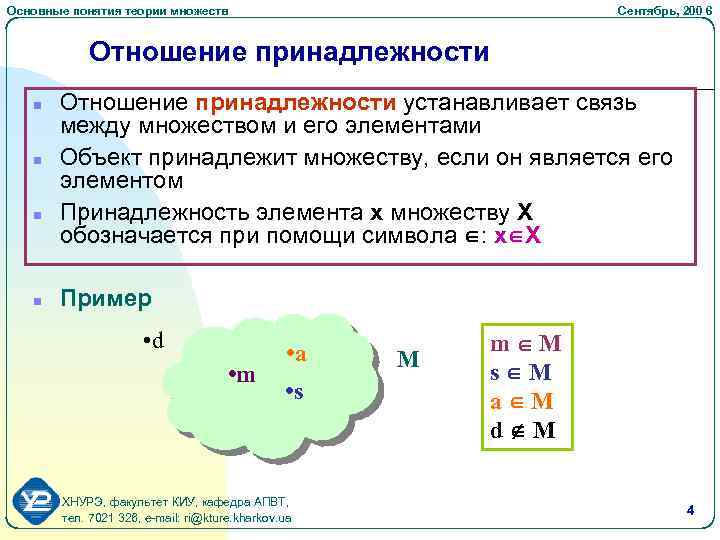
Основные понятия теории множеств Сентябрь, 200 6 Отношение принадлежности n n Отношение принадлежности устанавливает связь между множеством и его элементами Объект принадлежит множеству, если он является его элементом Принадлежность элемента x множеству X обозначается при помощи символа : x X Пример • d • m • a • s ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua M m M s M a M d M 4

Основные понятия теории множеств Сентябрь, 200 6 Отношение включения n n n Устанавливает связь между двумя множествами: (A B) ( m A m B) Обозначение: – строгое включение; – нестрогое включение А – подмножество множества В В – надмножество множества А Множества равны, если они состоят из одних и тех же элементов ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua А В A B 5

Основные понятия теории множеств Сентябрь, 200 6 Отношения принадлежности и включения: пример Дано множество A= {1, 2, 3, {3}, {4} }. Какие из следующих утверждений выполняются? n 2 A – верно, так как в множестве А есть элемент 2; n {1, 2} A – верно, так как в множестве А имеются элементы 1, 2, т. е. 1 A, 2 A ; n 3 A – верно, поскольку в множестве А есть элемент 3; n {3} A – верно, так как в множестве А есть элемент {3}; n 4 A – не выполняется, так как в множестве А нет элемента 4; n {4} A – верно, так как в множестве А имеется элемент {4}; n {4} A – не выполняется, поскольку в множестве А нет элемента 4, т. е. 4 A. ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua A • 2 • 1 • 3 • 4 2 A {1, 2} A 3 A {3} A 4 A {4} A 6

Основные понятия теории множеств Сентябрь, 200 6 Мощность множества. Пустое и универсальное множества n n Мощность множества или кардинальное число определяет количество элементов данного множества Обозначения: |M|, card M Пустое множество не содержит ни одного элемента: | |=0 Универсальное множество U – надмножество всех множеств: М U ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 7

Основные понятия теории множеств Сентябрь, 200 6 Булеан. Мощность булеана n n n Булеан – множество всех подмножеств данного множества M Обозначение: B(M) Пример: дано множество A={a, b, c}. Найти В(А). B(A)={ , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} } n n Мощность булеана определяется по формуле: |B(M)|=2 |M| Если А В и А≠В, то А – собственное подмножество множества В Пустое множество и само множество являются несобственными подмножествами множества М Остальные подмножества – собственные ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 8

Основные понятия теории множеств Сентябрь, 200 6 Операции над множествами Название операции Определение Пересечение A B={ x | x A и x B } Объединение A B={ x | x A или x B } Диаграммы Эйлера Разность Дополнение Симметрическая разность AB={ x | x A и x B } A=UA={ x | x U и x A } A∆B=(AB) (BA)= =(A B)(A B) ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua А В A B A A A B 9

Основные понятия теории множеств Сентябрь, 200 6 Тест-вопросы 1. Могут ли повторяться элементы множества? а) да; б) нет. 2. Является ли множество несобственным подмножеством самого себя? а) да; б) нет. 3. Множества равны, если они содержат а) одни и те же элементы; б) одинаковое количество элементов. ХНУРЭ, факультет КИУ, кафедра АПВТ, тел. 7021 326, e-mail: ri@kture. kharkov. ua 4. Являются ли понятия «мощность» и «кардинальное число» идентичными? а) да; б) нет. 5. Определить мощность булеана множества F={a, {d, c} }: А) |B(F)|= 2; Б) |B(F)|= 4; В) |B(F)|= 0; Г) |B(F)|= 3. 10
2_Множества.ppt