Основные понятия начертательной геометрии Точка прямая на комплексном

Основные понятия начертательной геометрии. Точка, прямая на комплексном чертеже Авторы: Бубеев И. Т. , Прудова Л. Ю.

Литература 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Локтев О. В. Краткий курс начертательной геометрии: Учеб. для втузов – М. : 2001. – 136 с. Гордон В. О. и др. Курс начертательной геометрии – М. : 2009. – 272 с. Чекмарев А. А. Инженерная графика: М. , 1998, 2002, 2004, 2007, 2008 Аристов В. М. , Аристова Е. П. Инженерная графика –М. : 2006. – 256 с. Лагерь А. И. Инженерная графика: Учеб. для вузов. . - М. : 2004. -334 с. Рогов С. В. Курс черчения с картами программированного контроля. – М. : 1990. – 432 с. Чекмарев А. А. , Осипов В. К. Справочник по машиностроительному черчению – М. : Высшая школа, 2007. – 493 с. Государственные стандарты «Единая система конструкторской документации ЕСКД» . , ГОСТы 1969 -2007 Начертательная геометрия: Учебно-методическое пособие с вариантами заданий для СРС/ Прудова Л. Ю. , Бубеев И. Т. , Мадуева С. Т. : Улан-Удэ, Изд-во ВСГУТУ, 2011 г. Доржиев Ц. Ц. , Чистяков Ф. К. , Аюшеев Т. В. Курс лекций по начертательной геометрии: Улан-Удэ, Изд-во ВСГУТУ, 2013 г.

• Начертательная геометрия изучает пространственные фигуры по их проекционным изображениям • Основной задачей НГ является разработка способов решения позиционных, метрических и др. задач по комплексному чертежу различных объектов

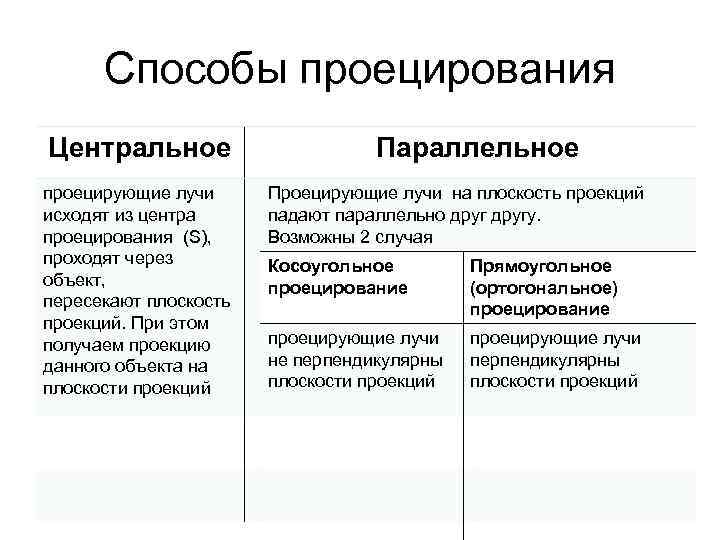Способы проецирования Центральное проецирующие лучи исходят из центра проецирования (S), проходят через объект, пересекают плоскость проекций. При этом получаем проекцию данного объекта на плоскости проекций Параллельное Проецирующие лучи на плоскость проекций падают параллельно другу. Возможны 2 случая Косоугольное проецирование Прямоугольное (ортогональное) проецирование проецирующие лучи не перпендикулярны плоскости проекций проецирующие лучи перпендикулярны плоскости проекций

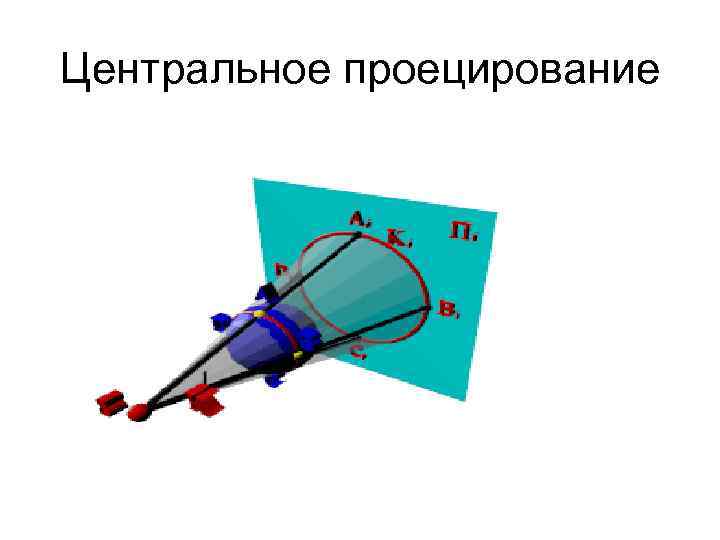Центральное проецирование

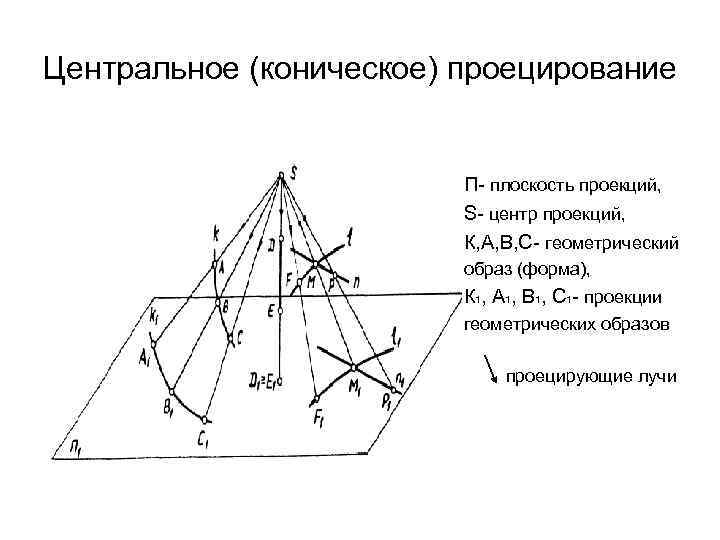Центральное (коническое) проецирование П- плоскость проекций, S- центр проекций, К, А, В, С- геометрический образ (форма), К 1, А 1, В 1, С 1 - проекции геометрических образов проецирующие лучи

Основные свойства центрального проецирования 1. Любая точка (кроме S) проецируется на плоскость проекций в единственную точку. 2. Каждой точке (A, B, C, . . . ), принадлежащей какой-либо линии (кривой или прямой), соответствует проекция (A 1, B 1, C 1, . . . ) этой точки на проекции данной линии.

3. Кривая в общем случае проецируется в кривую, а прямая - в прямую. Если прямая совпадает с проецирующим лучом (DE), то она проецируется в точку (D 1=E 1). Плоскость, проходящая через центр проекций, проецируется в прямую и называется проецирующей. Кривая, все точки которой принадлежат проецирующей плоскости, проецируется в прямую. 4. Точка пересечения линий проецируется в точку пересечения проекций этих линий (ℓ ∩ n = M).

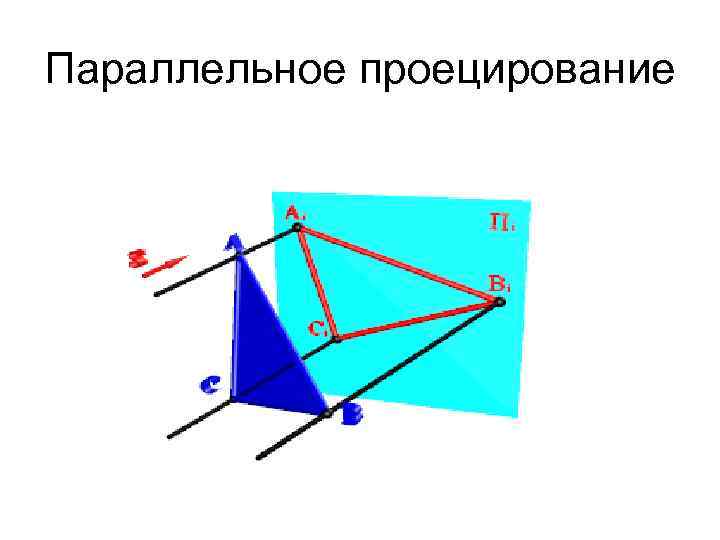Параллельное проецирование

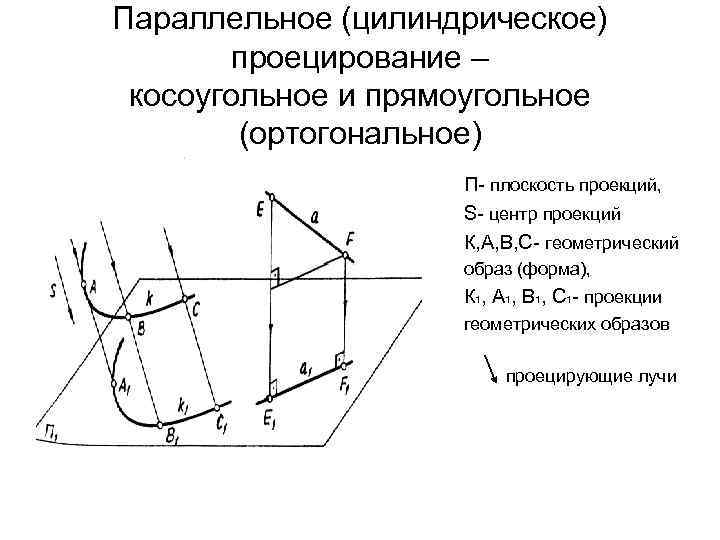Параллельное (цилиндрическое) проецирование – косоугольное и прямоугольное (ортогональное) П- плоскость проекций, S- центр проекций К, А, В, С- геометрический образ (форма), К 1, А 1, В 1, С 1 - проекции геометрических образов проецирующие лучи

Свойства параллельного проецирования 1. Проекцией точки на плоскость является точка. 2. Проекцией прямой линии на плоскость является прямая. 3. Если точка принадлежит линии, то проекция точки принадлежит проекции этой линии.

4. Проекциями параллельных прямых являются параллельные прямые. 5. Если отрезок прямой линии делится точкой в каком-либо отношении, то и проекция отрезка делится проекцией точки в том же отношении. 6. Проекция фигуры не меняется при параллельном переносе плоскости проекций.

Для ортогонального проецирования характерны ещё два свойства • 7. Прямой угол проецируется в натуральную величину, если одна из прямых, его образующих, параллельна плоскости проекций, а другая не перпендикулярна ей. • 8. Длина отрезка равна длине его проекции, деленной на косинус угла наклона отрезка прямой к плоскости

Условные обозначения а, b, c, d… – прямые, А, B, C, D…(1, 2, 3, 4…)- точки, Γ(гамма), Δ(дельта), Θ(тэта), Λ(ламбда), Ρ(ро)- плоскости, поверхности, П 1, П 2, П 3 - плоскости проекции, ≡ - совпадение, || - параллельны, - скрещиваются, - перпендикулярны ∩ - пересекает - принадлежит - провести через (включение)

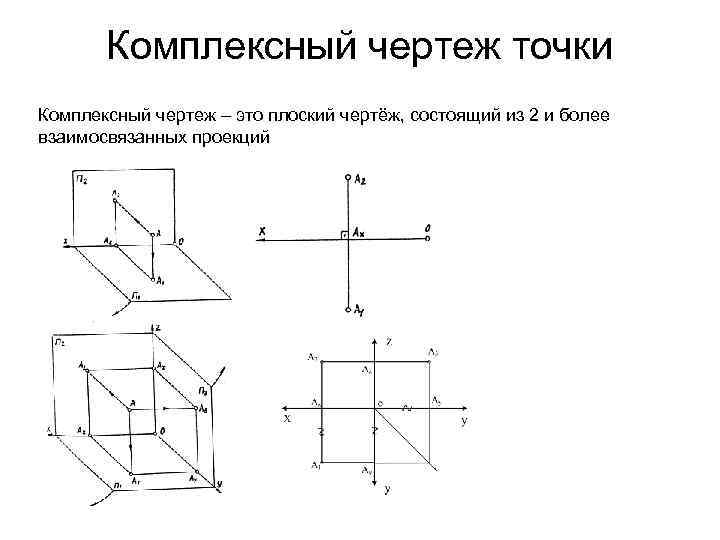Комплексный чертеж точки Комплексный чертеж – это плоский чертёж, состоящий из 2 и более взаимосвязанных проекций

Основные требования к проекционным изображениям 1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой; 2. Наглядность – чертеж должен создавать пространственное представление о форме предмета; 3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты; 4. Простота – изображение должно быть простым по построению и должно допускать однозначное описание объекта в виде последовательности графических операций.

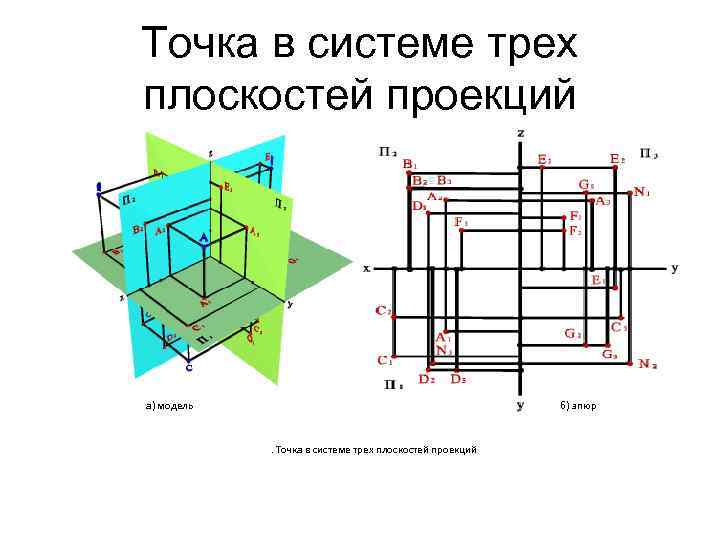Точка в системе трех плоскостей проекций а) модель б) эпюр . Точка в системе трех плоскостей проекций

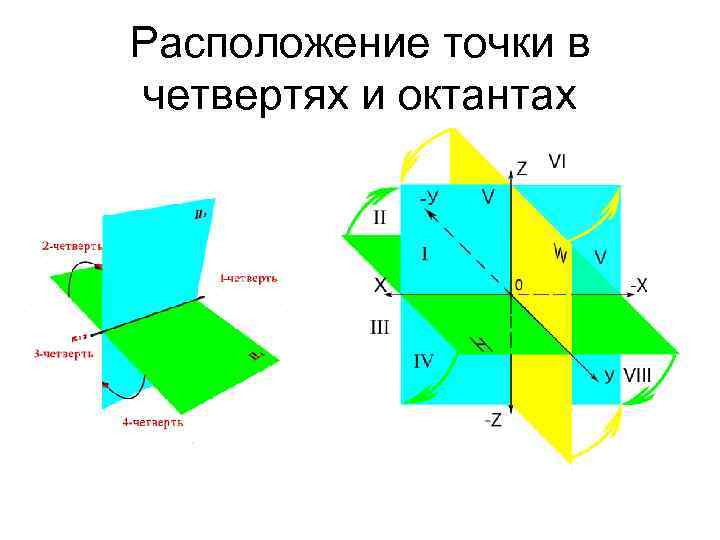Расположение точки в четвертях и октантах

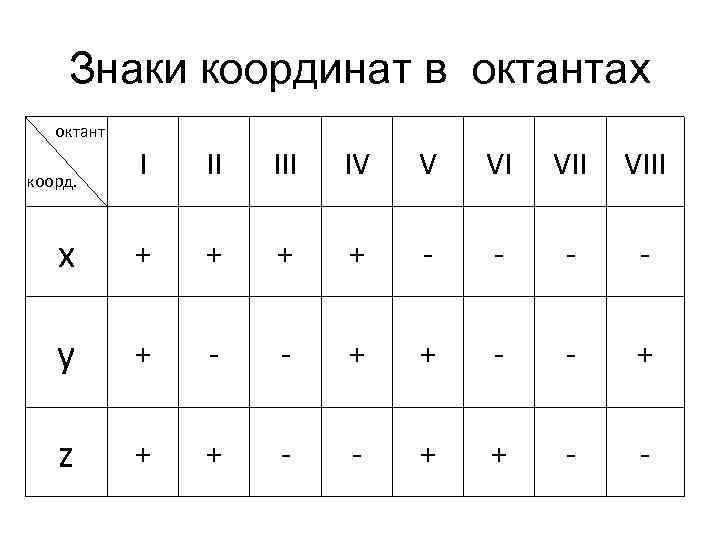Знаки координат в октантах октант коорд. I II IV V VI VIII x + + - - y + - - + z + + - -

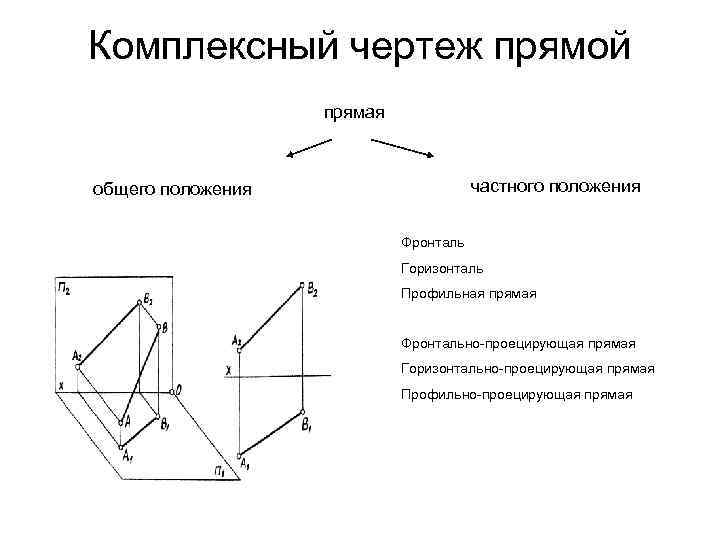Комплексный чертеж прямой прямая частного положения общего положения Фронталь Горизонталь Профильная прямая Фронтально-проецирующая прямая Горизонтально-проецирующая прямая Профильно-проецирующая прямая

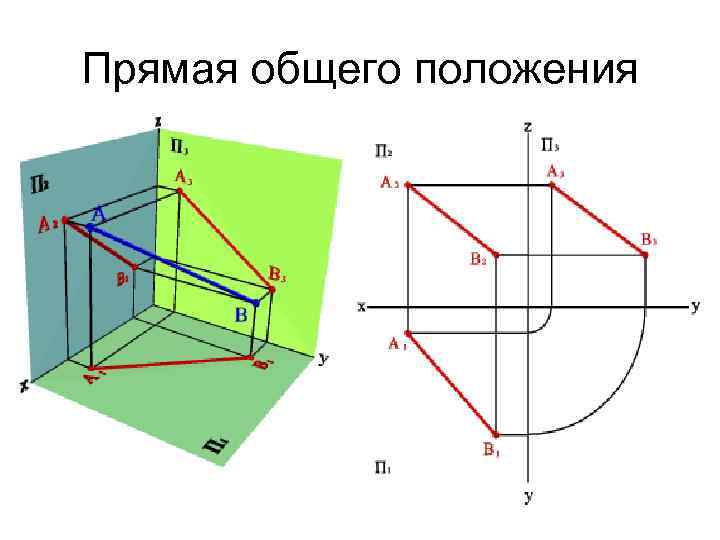Прямая общего положения

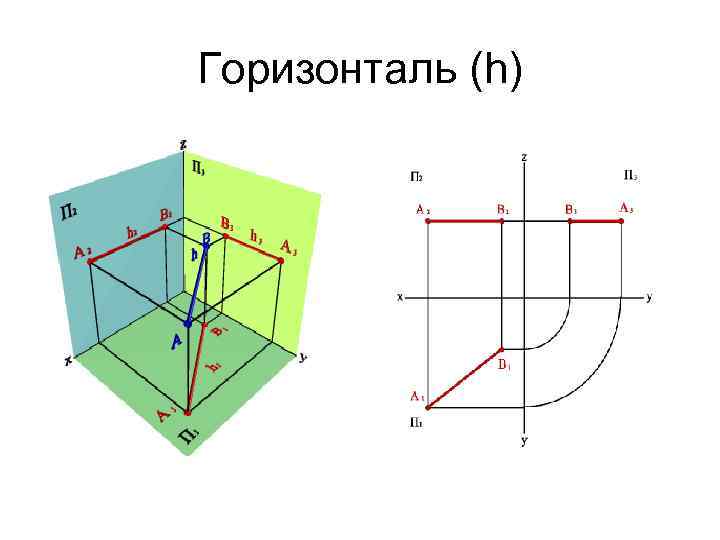Горизонталь (h)

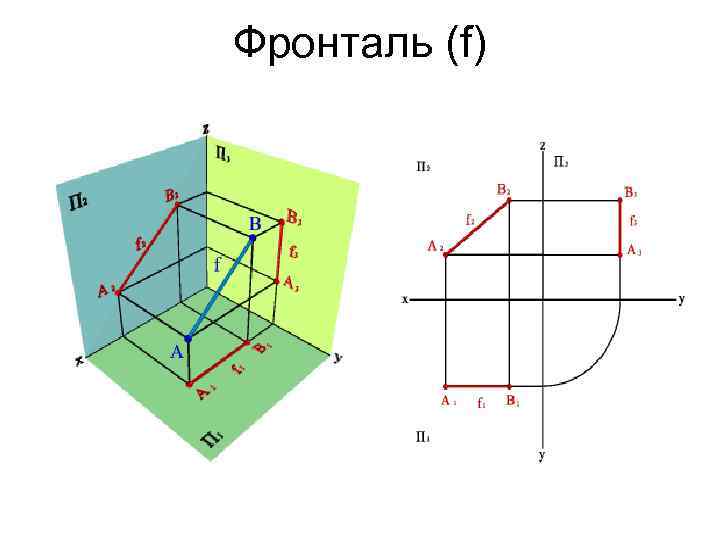Фронталь (f)

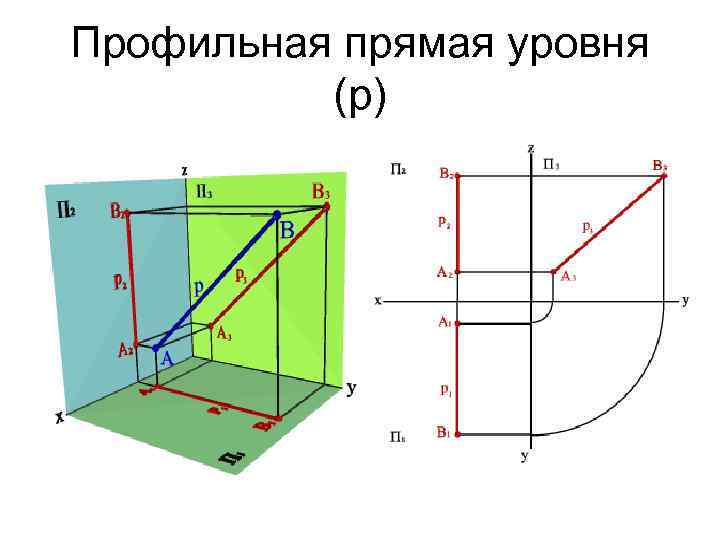Профильная прямая уровня (p)

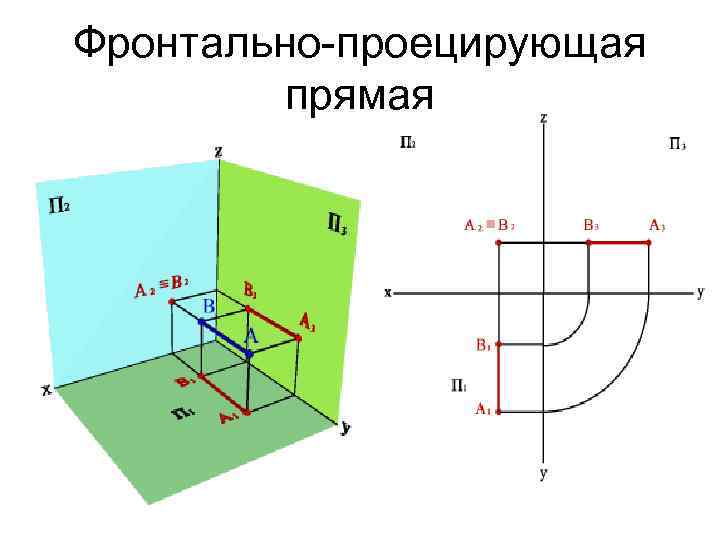Фронтально-проецирующая прямая

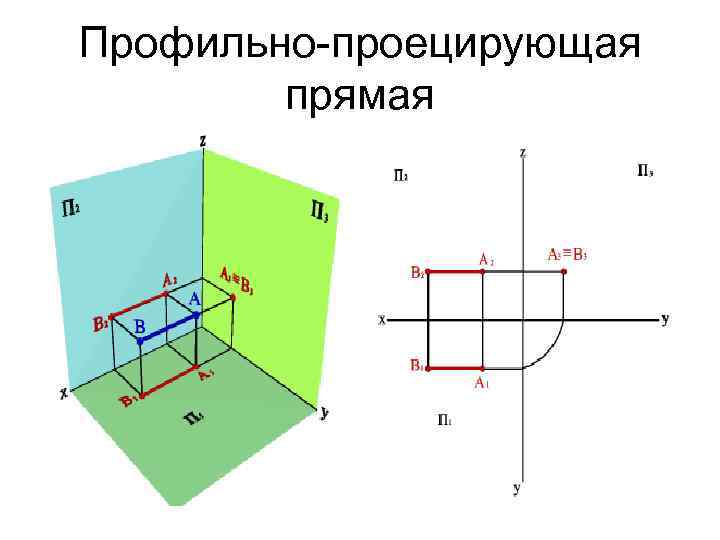Профильно-проецирующая прямая

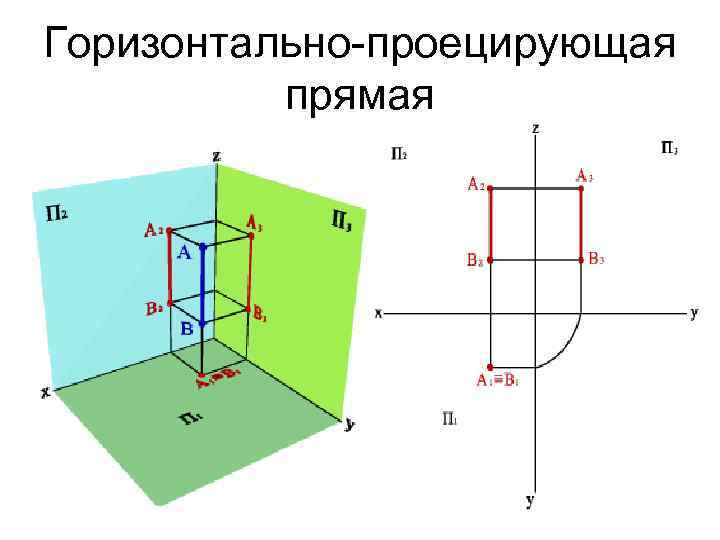Горизонтально-проецирующая прямая

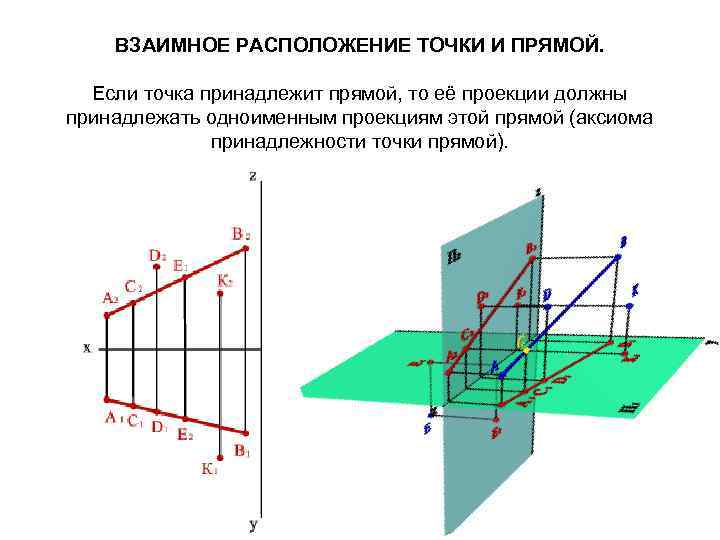ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПРЯМОЙ. Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой).

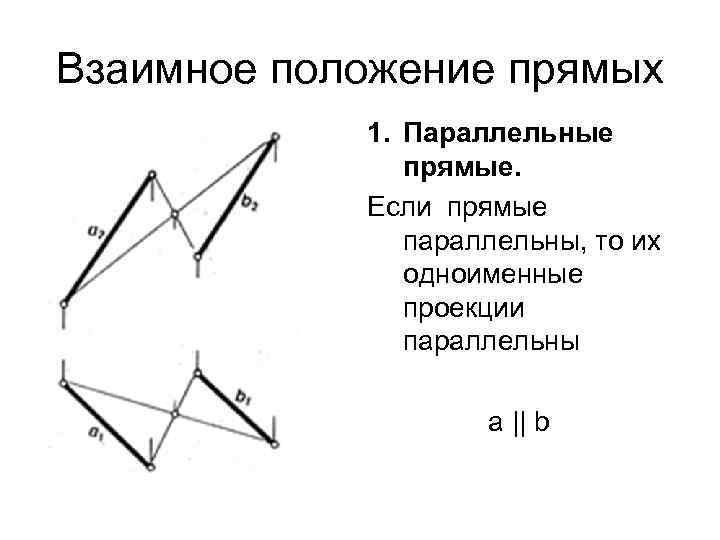Взаимное положение прямых 1. Параллельные прямые. Если прямые параллельны, то их одноименные проекции параллельны a || b

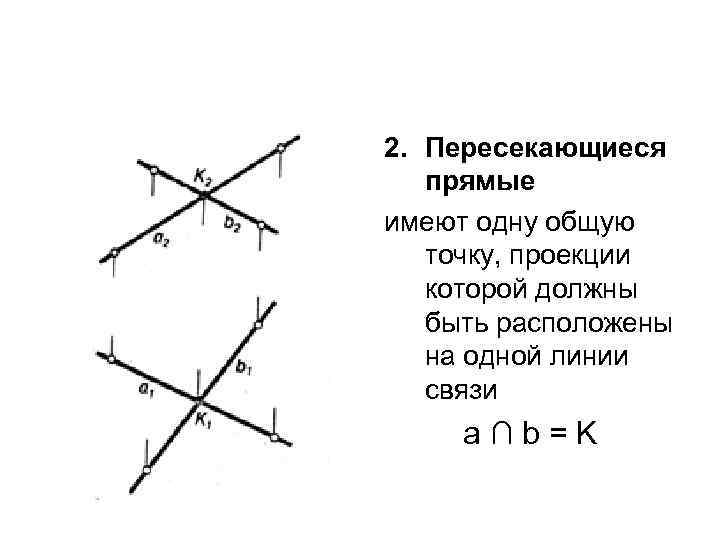2. Пересекающиеся прямые имеют одну общую точку, проекции которой должны быть расположены на одной линии связи a∩b=K

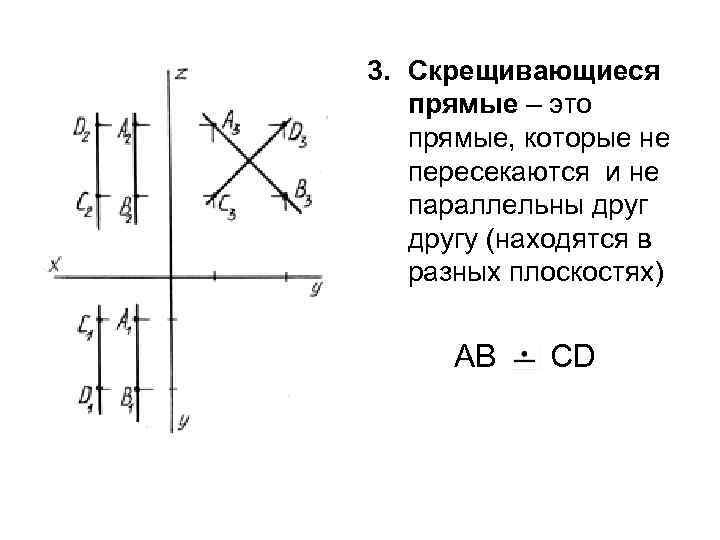3. Скрещивающиеся прямые – это прямые, которые не пересекаются и не параллельны другу (находятся в разных плоскостях) АВ СD

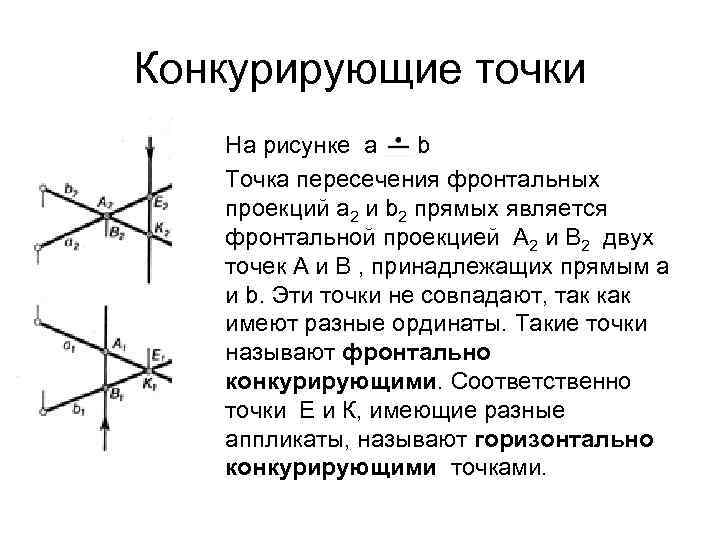Конкурирующие точки На рисунке a b Точка пересечения фронтальных проекций a 2 и b 2 прямых является фронтальной проекцией А 2 и В 2 двух точек А и В , принадлежащих прямым a и b. Эти точки не совпадают, так как имеют разные ординаты. Такие точки называют фронтально конкурирующими. Соответственно точки Е и К, имеющие разные аппликаты, называют горизонтально конкурирующими точками.