Основные понятия и законы физики Л 12 Квантование

Основные понятия и законы физики Л. 12 Квантование энергии Самое полное на сегодня описание свойств вещества даёт квантовая физика. Вот некоторые её основные результаты: При финитном движении частиц их энергия квантуется, т. е. принимает не какие угодно, а строго определённые значения Частица с данной энергией (на данном энергетическом уровне) движется, находясь на определённой орбитали, т. е. вероятность обнаружения частицы распределена в пространстве определённым образом и не зависит от времени 1

Количественное микроскопическое описание – уравнение Шрёдингера и амплитуда вероятности Уравнение Шрёдингера (волновое уравнение)– вместо 2 -го закона Ньютона Свободная частица – инфинитное движение Амплитуда вероятности для свободной частицы – вместо радиус-вектора – плоская монохроматическая бегущая волна де Бройля (волна вероятности) 2

Амплитуда вероятности позволяет вычислить вероятность – базовое понятие физики 3 Плотность вероятности – вместо траектории, по которой частица движется с течением времени Малая вероятность того, что частица в момент t находится в малой области пространства dx вблизи x Условие нормировки плотности вероятности

4 Инфинитное движение квантовой частицы – бегущая волна де Бройля Финитное движение квантовой частицы – стоячая волна де Бройля – зависит от потенциальной энергии (приближённое) условие квантования Главное квантовое число (число узлов стоячей волны внутри резонатора)

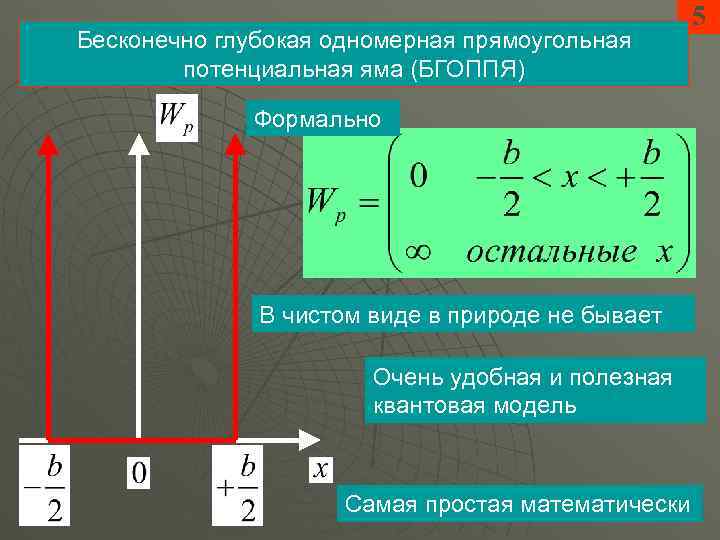Бесконечно глубокая одномерная прямоугольная потенциальная яма (БГОППЯ) Формально В чистом виде в природе не бывает Очень удобная и полезная квантовая модель Самая простая математически 5

Бесконечно глубокая одномерная прямоугольная потенциальная яма (БГОППЯ) Уровни энергии частицы в БГОППЯ 6

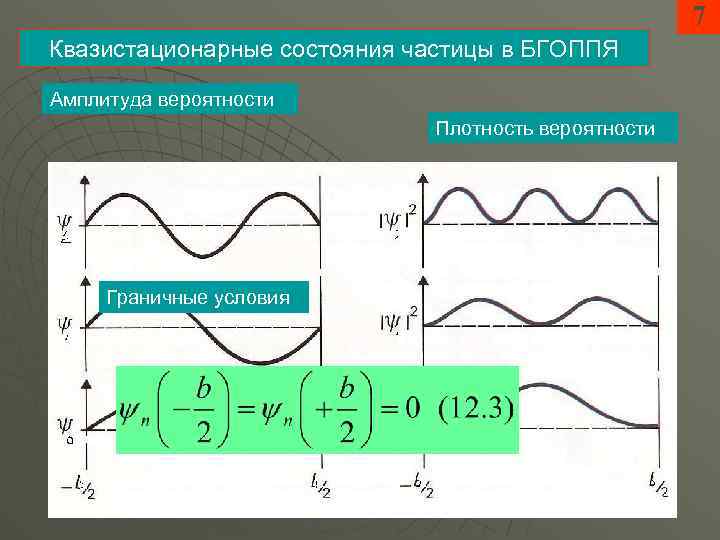7 Квазистационарные состояния частицы в БГОППЯ Амплитуда вероятности Плотность вероятности Граничные условия

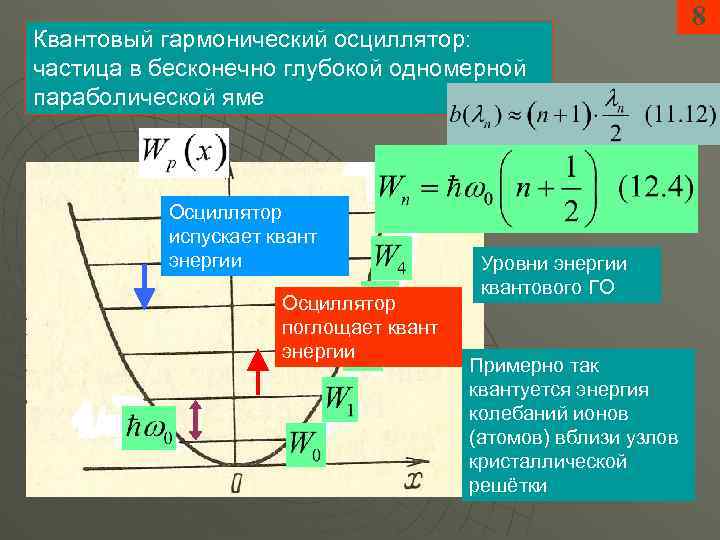Квантовый гармонический осциллятор: частица в бесконечно глубокой одномерной параболической яме Осциллятор испускает квант энергии Осциллятор поглощает квант энергии Уровни энергии квантового ГО Примерно так квантуется энергия колебаний ионов (атомов) вблизи узлов кристаллической решётки 8

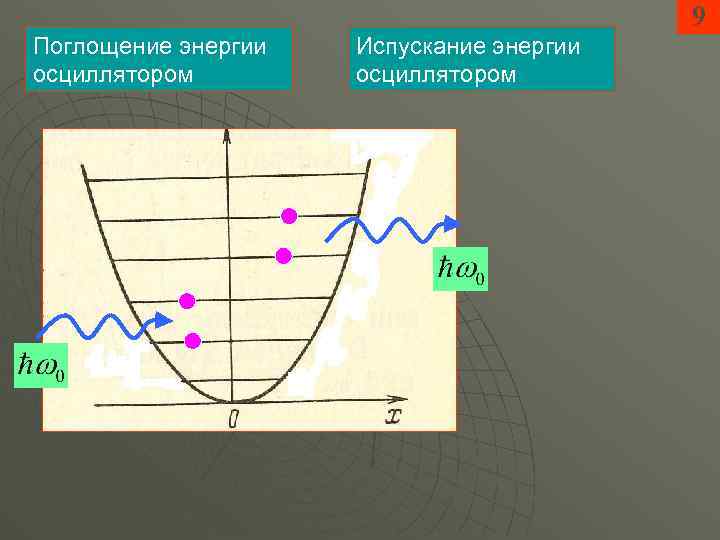9 Поглощение энергии осциллятором Испускание энергии осциллятором

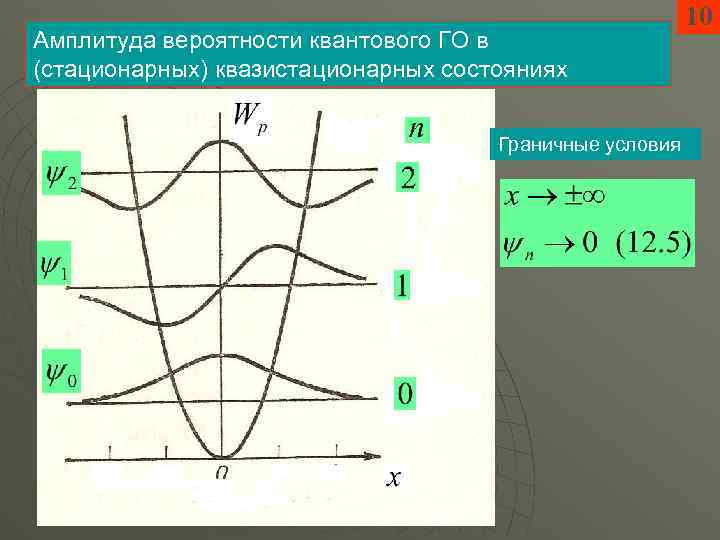Амплитуда вероятности квантового ГО в (стационарных) квазистационарных состояниях Граничные условия 10

11 Стационарное (основное) состояние, в этом состоянии частица может находиться вечно Квазистационарные (возбуждённые) состояния, в этих состояниях частица может находиться ограниченное время, после чего спонтанно переходит в более низколежащие состояния, испуская квант энергии Почему происходят переходы? Взаимодействие с квантовыми флуктуациями электромагнитного поля в вакууме: квантовая электродинамика (релятивистская квантовая теория поля)

Основные задачи классической механики (финитное движение): Основные задачи квантовой механики (финитное движение): Зависимость радиус -вектора частицы Энергии и амплитуды вероятности квазистационарных состояний Пример технической задачи: расчёт траектории полёта космического аппарата на Луну Пример технической задачи: расчёт «схемы» работы гелий-неонового лазера 12

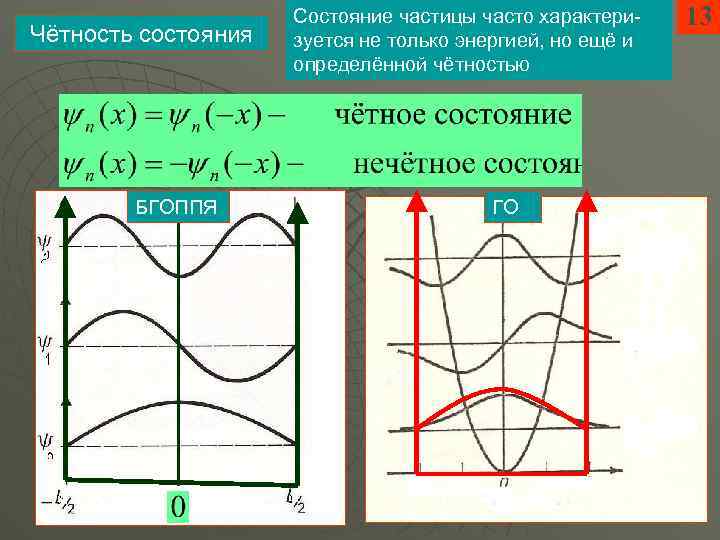Чётность состояния БГОППЯ Состояние частицы часто характеризуется не только энергией, но ещё и определённой чётностью ГО 13

Плотность вероятности позволяет вычислять любые средние значения по ансамблю Например 14

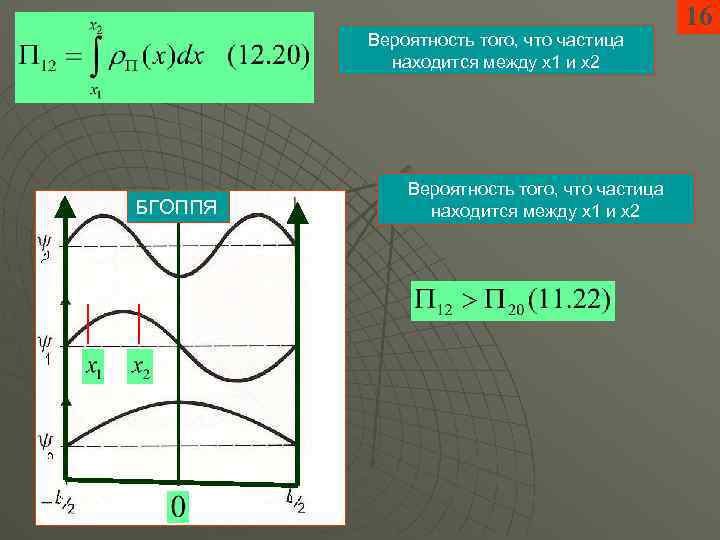Вероятность того, что частица находится между х1 и х2 БГОППЯ Вероятность того, что частица находится между х1 и х2 16

Cвязь этой лекции с вопросами ННЗ – буклет 3. 14. Волны де Бройля. Квантование как образование стоячих волн. 3. 15. Амплитуда вероятности и плотность вероятности. 3. 16. Схема энергетических уровней частицы в БГОППЯ. 3. 17. Схема энергетических уровней гармонического осциллятора. 3. 18. Уравнение Шрёдингера 24