Основные понятия электрохимии Термодинамика электрохимических систем Термодинамические

Основные понятия электрохимии Термодинамика электрохимических систем

Термодинамические функции в электрохимии Термодинамика электрохимических систем включает стандартный набор термодинамических функция, однако требует дополнительного учета заряда частиц и разности потенциалов T=const p=const H=U+p. V G=U+p. V-TS

Энергия Гиббса Самопроизвольно претекают процессы для которых ΔG<0 В равновесии минимальное значение энергии Гиббса (ΔG=0 или d. G=0) Энергия Гиббса является аддитивной функцией. Для чистых компонентов системы (т. е. формирующих фазу постоянного состава)

Химический потенциал Для фаз переменного состава вклад каждого компонента в энергию Гиббса данной фазы зависит не только от количества вещества, но и от концентрации Для малых изменений состава фазы химический потенциал компонента (Дж/моль)

Химический потенциал Для идеального газа Для разбавленных (идеальных) растворов В результате для фаз переменного состава

Электрохимический потенциал Энергия иона в данной среде зависит не только от химических взаимодействий (μj), но и от электростатических (± zj. Fψ). Поэтому вместо химического потенциала используют электрохимический потенциал Кстати, суммарная энергия Гиббса не зависит от электростатического потенциала. Действительно, если учесть условие электронейтральности, то в выражении G=∑nj μj слагаемые ± zj. Fψ сократятся.

Особенности электрохимических систем Электрохимический потенциал отдельного иона невозможно определить (т. к. всегда присутствуют несколько ионов, и в эксперементе измеряются суммарные свойства) Энергетические эффекты индивидуальных электродных реакций невозможно измерить (т. к. все реакции сопровождаются спаренной реакцией на противоположном электроде) и рассчитать (т. к. для расчёта требуются индивидуальные электрохимические потенциалы ионо и Гальвани-потенциал)

Понятие активности Для описания отклонений поведения реальных растворов от идеальных вводится понятие активности (Гильберт Льюис, 1907 г. ) Для твердых и однокомпонентных фаз ак=1 Коэффициент активности описывает отклонения систем от идеальных

ЭДС гальванической цепи Для химической реакции Аналогично для электродной реакции можно записать Имеем в виду, что здесь электроны находятся в металле при потенциале ψ(М), а ионы — в электролите при потенциале ψ(Е).

ЭДС гальванической цепи В равновесии Это обобщение известного выражения для случая протеканя химической реакции. Ни один из параметров уравнения не может быть определен экспериментально.

ЭДС гальванической цепи Для цепи из двух электродов, на которых происходит суммарная реакция с учётом того, что для каждого из электродов получаем Если ΔGm<0, то реакция протекает самопроизвольно, т. е. цепь работает ка источник тока, а электрод (1) будет анодом (отрицательным электродом)

ЭДС гальванической цепи ЭДС данной цепи есть сумма Гальванипотенциалов на границах раздела. с учётом того, что для каждой границы раздела получаем После упрощения с учетом получим

ЭДС гальванической цепи ЭДС гальванической цепи связана с изменением энергии Гиббса суммарной реакции. Это также следует из первого закона термодинамики, т. к. это максимальная полезная (электрическая работа), а она равна. Типично, что в выражении для ЭДС все слагаемые, содержащие хим. потенциал электронов в электродах попарно сокращаются, поскольку следует учитывать также перенос электронов через границу металл.

ЭДС гальванической цепи Получается, что для нерасходующихся электродов ЭДС не зависит от материала электрода, а только от типа реакции (для Гальвани-потенциалов было наоборот). Например: ток не течет! ЭДС=0 потенциалы электродов одинаковые гальвани-потенциалы разные Поэтому часто при записи ЭДС и потенциалов электродов указывают только сами реакции

Зависимость электродных потенциалов от концентрации Электродные потенциалы и ЭДС цепей зависят от состава электролита Е=φG+const константа; зависит от природы реакции; равна ЭДС при с=1 М RT/F = 0, 02569 V 2, 303 RT/F = 0, 05916 V (~59 м. В) потенциалопределяющие вещества СOx E СRed E

Уравнение Нернста Впервые уравнение такого типа предложил Вальтер Нернст в 1869 г. для реакции Сейчас все уравнения такого типа называют Уравнением Нернста

Уравнение Нернста в реальных системах В реальных системах определить активности отдельных ионов невозможно, поэтому используют среднюю активность ионов: Ea 0 - стандартный электродный потенциал; Ec 0 — формальный электродный потенциал

Пример таблицы стандартных потенциалов

Электроды второго рода Пример: серебро в растворе KCl

Электроды второго рода Так концентрация ионов серебра контролируется концентрацией хлорид-ионов, то в результате только они участвуют в записи уравнении для потенциала электрода. Достаточно просто поддерживать постоянную концентрацию хлорид-ионов (например, поместить проволоку в насыщенный раствор KCl). Растворение/осаждение серебра в процессе реакции не изменит концентрацию Cl- (а, значит, и потенциал).

Электроды второго рода чаще всего используются в качестве электродов сравнения

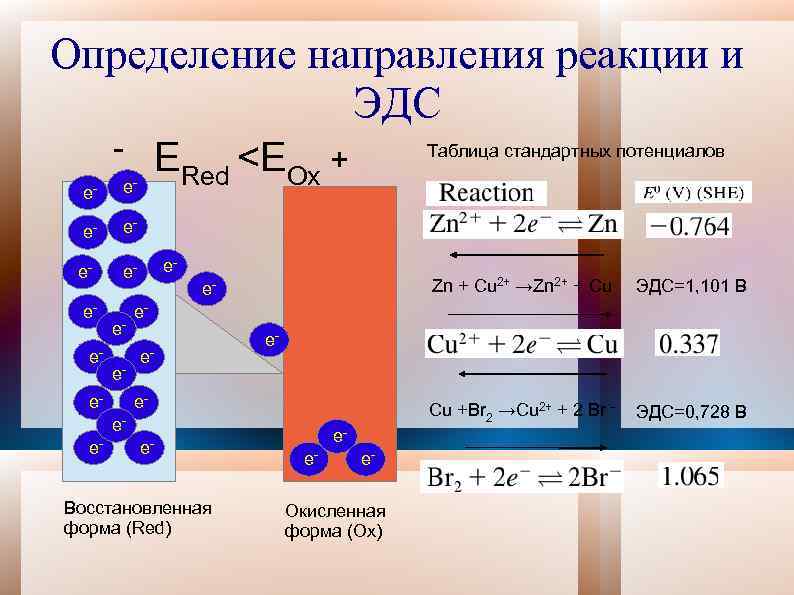Определение направления реакции и ЭДС e- e- ERed

Зависимость потенциалов от р. Н Часто в уравнение реакции входят Н+ или ОНно Поэтому можно формулировать реакции двумя эквивалентными способами Также существуют два эквивалентных способа расчета электродного потенциала SHE (с. в. э. ), p. H 2=1, a. H+=1, E≡ 0

Диаграммы Пурбэ Часто при различных р. Н могут существовать разные формы продуктов. При этом меняется и стандартный потенциал реакции.

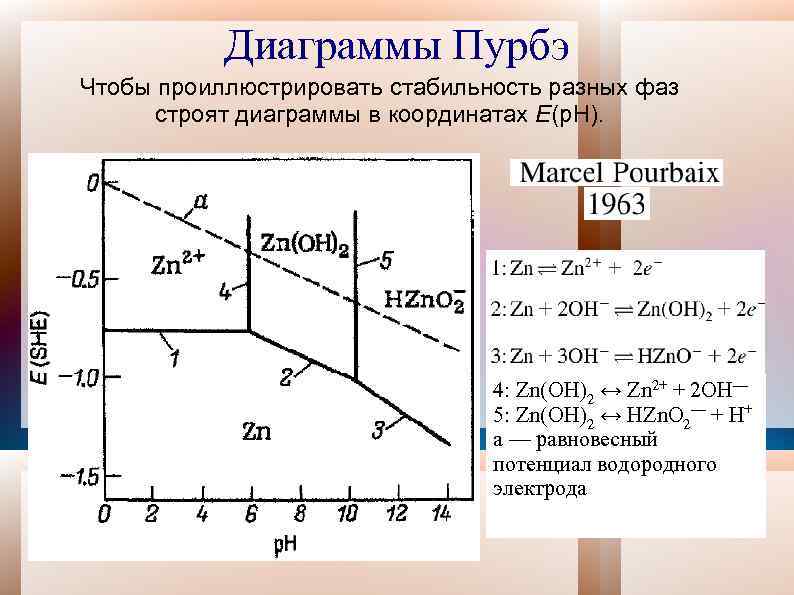Диаграммы Пурбэ Чтобы проиллюстрировать стабильность разных фаз строят диаграммы в координатах E(p. H). 4: Zn(OH)2 ↔ Zn 2+ + 2 OH— 5: Zn(OH)2 ↔ HZn. O 2— + H+ a — равновесный потенциал водородного электрода

Зависимость стандартных потенциалов от температуры По уравнению Гиббса-Гельмгольца Таким образом, температурный коэффициент ЭДС зависит от изменения энтропии токопроизводящей реакции. Меняются Гальвани-потенциалы на всех границах раздела (в т. ч. для электрода сравнения) — не измерить. Попытка измерить ЭДС ячейки с разными температурами катодного и анодного пространства приводит к возникновению разности потенциалов в проводнике (эффект Томсона, 1856 г. ) Измеряемые величины температурного коэффициента потенциала зависят от электрода сравнения. По договору температурный коэффициент с. в. э. = 0, т. е. Ea 0 (H+, H 2)=0 при любой температуре. Для других электродов сравнения они внесены в таблицы.

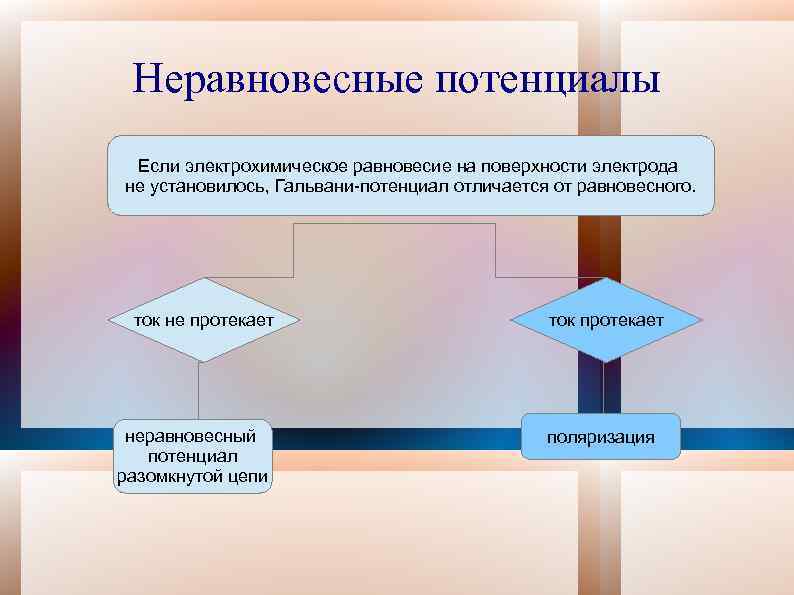Неравновесные потенциалы Если электрохимическое равновесие на поверхности электрода не установилось, Гальвани-потенциал отличается от равновесного. ток не протекает неравновесный потенциал разомкнутой цепи ток протекает поляризация

Неравновесные потенциалы разомкнутой цепи невозможно протекание никаких электродных реакций в данных условиях маленькие токи обмена основной реакции Одновременно протекают несколько реакций потенциал определяют побочные процессы потенциал определяет заряжение ДЭС идеально поляризуемый электрод смешанный потенциал неравновесный потенциал разомкнутой цепи

Потенциалы электрода при протекании тока Протекает ненулевой ток Парциальные токи отличаются от равновесных; для этого требуется изменение баланса электрических и химических сил, т. е. электрическая сила fe должна быть больше или меньше химической силы fch Изменение баланса сил приведёт к сдвигу потенциала (поляризации). Анодному току соответствует положительный сдвиг потенциала, катодному — отрицательный. Заметная поляризация наблюдается, если ток больше тока обмена.

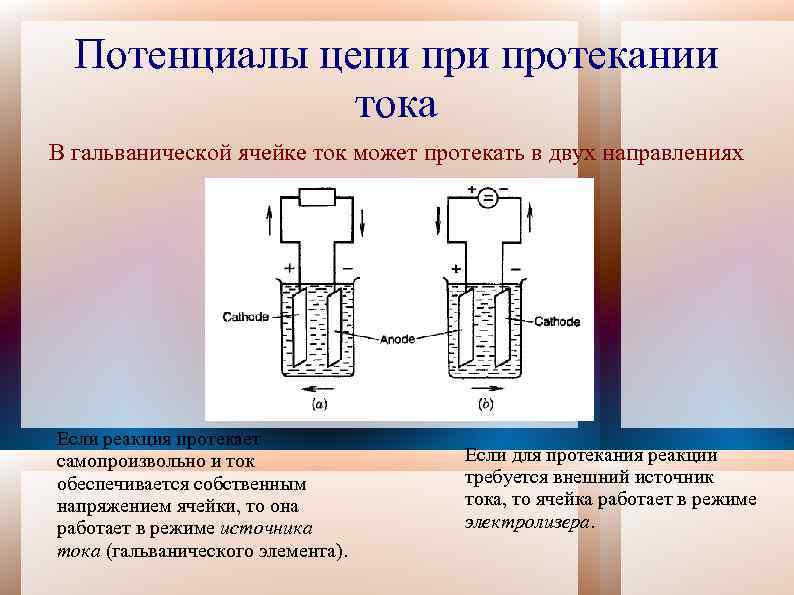Потенциалы цепи протекании тока В гальванической ячейке ток может протекать в двух направлениях Если реакция протекает самопроизвольно и ток обеспечивается собственным напряжением ячейки, то она работает в режиме источника тока (гальванического элемента). Если для протекания реакции требуется внешний источник тока, то ячейка работает в режиме электролизера.

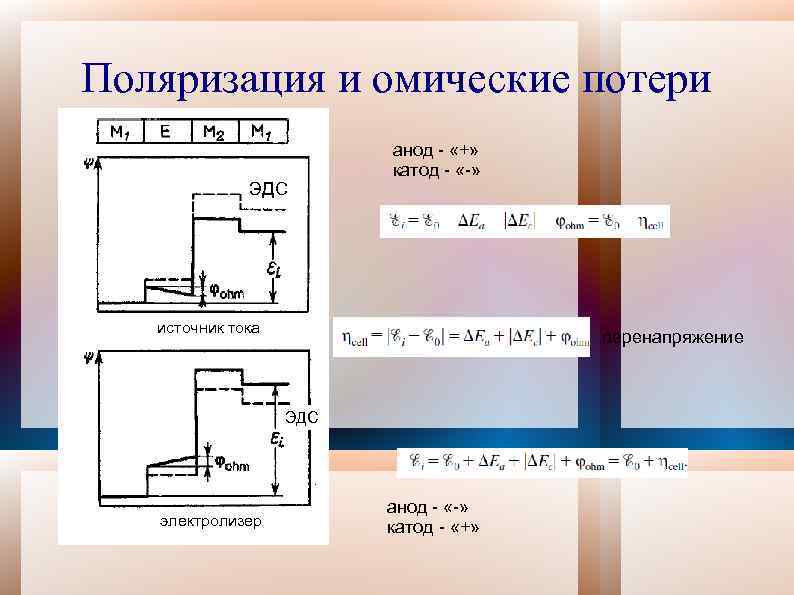Поляризация и омические потери ЭДС анод - «+» катод - «-» источник тока перенапряжение ЭДС электролизер анод - «-» катод - «+»

Массоперенос

Природа отдельных стадий электродного процесса и их последовательность 1. Химическая стадия 2. Массоперенос 1 2 e- Red 3 2 Red A Ox Ox B 1 3. Электрохимическая стадия Массоперенос - поставка реагентов (отвод продуктов) к (от) поверхности реакции - электроду, на котором протекает та или другая электрохимическая реакция. 33

Тип массопереноса 1. Диффузия 2. Конвекция 3. Миграция 34

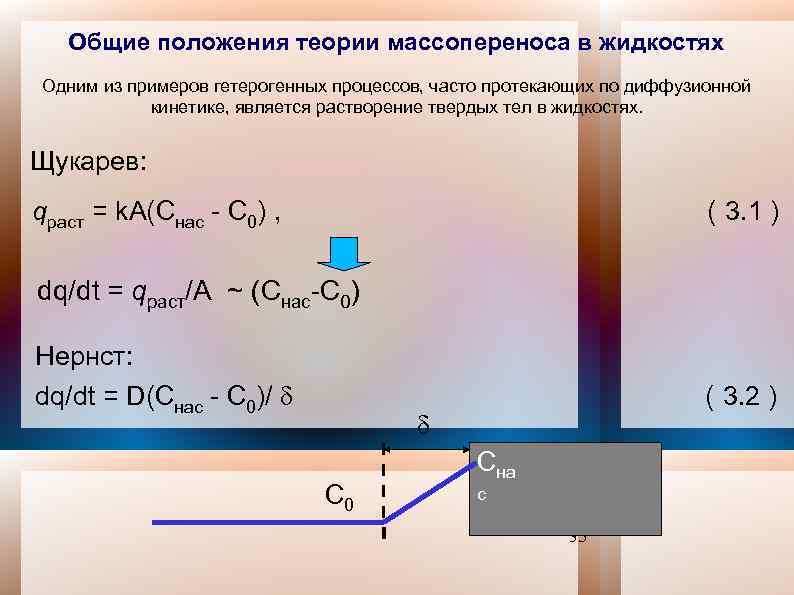Общие положения теории массопереноса в жидкостях Одним из примеров гетерогенных процессов, часто протекающих по диффузионной кинетике, является растворение твердых тел в жидкостях. Щукарев: qраст = k. А(Cнас - C 0) , ( 3. 1 ) dq/dt = qраст/А ~ (Cнас-C 0) Нернст: dq/dt = D(Cнас - C 0)/ ( 3. 2 ) Сна с С 0 35

Общие положения теории массопереноса в жидкостях Явления переноса могут быть описаны в рамках линейных соотношений между потоками и «действующими силами» . Бинарный электролит и существование градиента электрохимического потенциала i по ионным (i-ым) компонентам системы: Ji = - (Di. Сi /RT) grad i , i = +, - ( 3. 1. 1 ) i = 0 i+RTln. Сi+zi. FФ Ji = - Di grad Сi - (zi Di F/RT)Сi grad Ф ( 3. 1. 2 ) zi=0 I закон Фика Ji = - Di grad Сi ( 3. 1. 3 ) 36

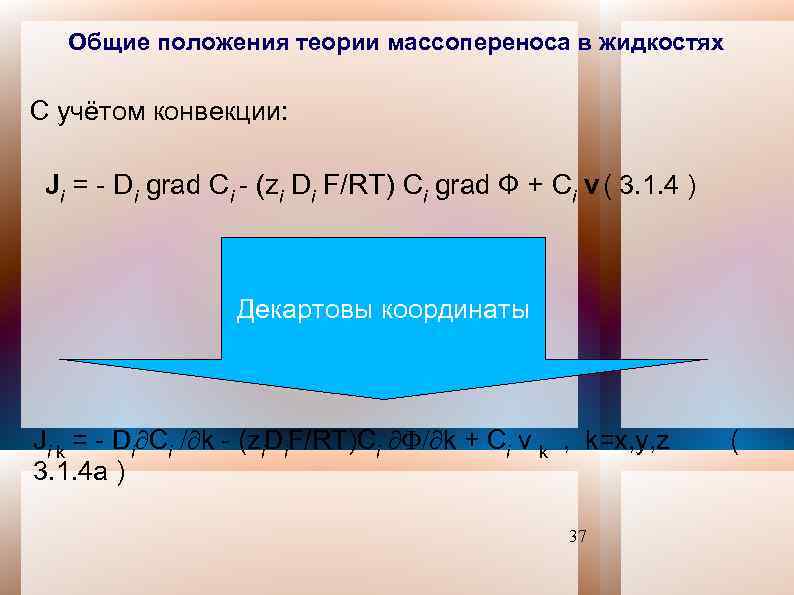Общие положения теории массопереноса в жидкостях С учётом конвекции: Ji = - Di grad Сi - (zi Di F/RT) Сi grad Ф + Сi v ( 3. 1. 4 ) Декартовы координаты Ji k = - Di Сi k - (zi. Di. F/RT)Сi k + Сi v k , k=x, y, z ( 3. 1. 4 a ) 37

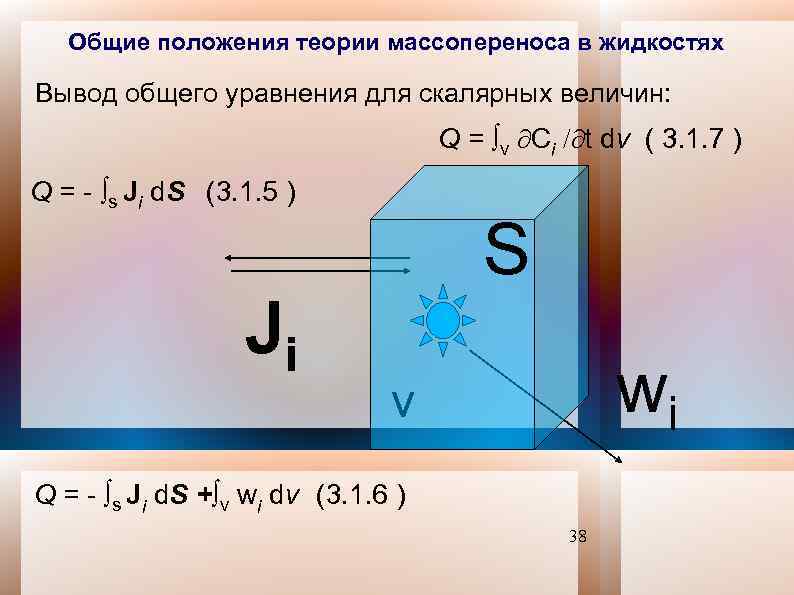Общие положения теории массопереноса в жидкостях Вывод общего уравнения для скалярных величин: Q = v Сi t dv ( 3. 1. 7 ) Q = - s Ji d. S (3. 1. 5 ) Ji S wi v Q = - s Ji d. S + v wi dv (3. 1. 6 ) 38

Общие положения теории массопереноса в жидкостях Q |v = Q |S - s Ji d. S + v wi dv = v Сi t dv (3. 1. 8 ) Теорема Гаусса-Остроградского S Ji d. S = v div Ji dv - v (div Ji - wi) dv = v Сi t dv (3. 1. 9 ) Сi t = div Ji - wi (3. 1. 10 ) 39

Общие положения теории массопереноса в жидкостях Сi t = div Ji - wi (3. 1. 9 ) Ji = - Di grad Сi - (zi Di F/RT) Сi grad Ф + Сi v ( 3. 1. 4 ) Сi t = div[Digrad. Сi]+div[(zi Di. F/RT)Сigrad. Ф]-div(Сiv)+wi ( 3. 1. 11 ) Если Di=const то div [Di grad Сi] = Di div grad Сi = Di Сi; кроме того div (С I) = (I grad)С + С div I i i i Сi t = Di Сi + (zi Di F/RT)Сi Ф + (zi Di F/RT)(grad Фgrad)Сi - Сi div v -(v grad)Сi + wi несжимаемость жидкости div v = 0 Сi t = Di Сi + (zi. Di. F/RT)Сi Ф + (zi. Di. F/RT)(grad. Фgrad)Сi -(vgrad)Сi + wi ( 3. 1. 12 ) 40

Общие положения теории массопереноса в жидкостях В декартовых координат x, y, z Сi t = Di{ 2 Сi z 2 + 2 Сi y 2 + 2 Сi x 2} + (zi. Di. F/RT)Сi{ 2 z 2 + 2 y 2 + 2 x 2} (zi. Di. F/RT){ Сi z z Сi y y Сi x x}- vz Сi z - vy Сi y - vx Сi x + wi ( 3. 1. 13 ) wi = Cj - Ci , ( 3. 1. 14 ) 41

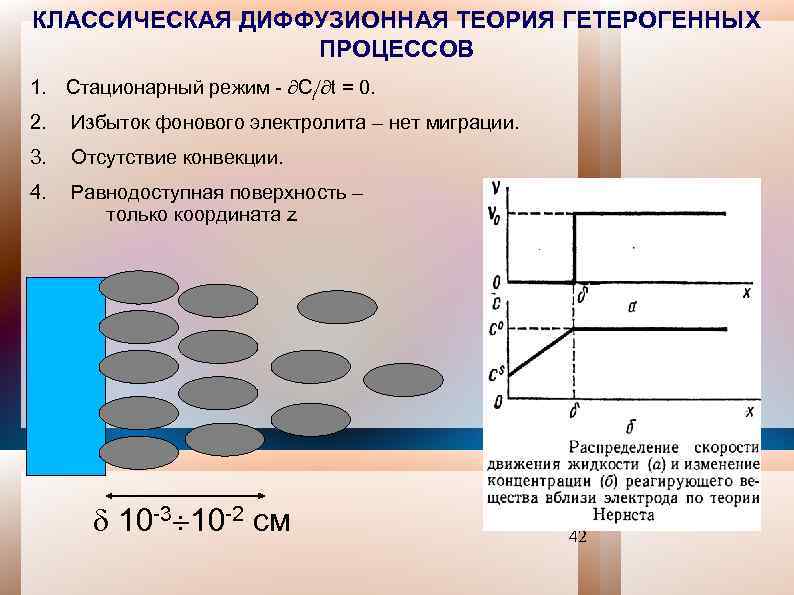КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ 1. Стационарный режим - Сi t = 0. 2. Избыток фонового электролита – нет миграции. 3. Отсутствие конвекции. 4. Равнодоступная поверхность – только координата z 10 -3 10 -2 см 42

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ Сi t = Di{ 2 Сi z 2 + 2 Сi y 2 + 2 Сi x 2} + (zi. Di. F/RT)Сi{ 2 z 2 + 2 y 2 + 2 x 2} (zi. Di. F/RT){ Сi z z Сi y y Сi x x}vz Сi z - vy Сi y - vx Сi x + wi ( 3. 1. 13 ) Di d 2 Ci(z) dz 2 = 0 , 0 z ( 3. 2. 1 ) 43

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ «краевые» условия: Ci( ) = C 0 i ( 3. 2. 2 ) Ji k = - Di Сi k - (zi. Di. F/RT)Сi k + Сi v k , k=x, y, z ( 3. 1. 4 a ) Ji = - Di d. Ci(z) dz при z = 0, ( 3. 2. 3 ) Тогда Di d 2 Ci(z) dz 2 = 0 , 0 z ( 3. 2. 1 ) ∫ Ji = - Di d. Ci(z) dz , но уже при любом z ( 3. 2. 4 44

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ А Ji(z 1) = А Ji(z 2). Jiz Ci(0) А 0 z 1 А Ji(z 1) = Ji(z 2), C 0 i Jix = Jiy = 0 z 2 Ji независим от z z Ji = - Di d. Ci(z) dz ( 3. 2. 4 )∫ Ci(z) = Const - Ji z /Di ( 3. 2. 5 ) Ci( ) = C 0 i Ji = Di[Ci(0) - C 0 i]/ ( 3. 2. 7 ) Ci(z) = C 0 i - Ji (z - )/Di ( 3. 2. 6 ) 45

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ Ji = Di[Ci(0) - C 0 i]/ ( 3. 2. 7 ) ? ? Нернст: 1. = const (не зависит от скорости процесса) 2. Ci(0) = Cнас Ji = Di[Cнас - C 0 i]/ ( 3. 2. 8 ) k = Di/ qраст = k. А(Cнас - C 0) ( 3. 1 ) 46

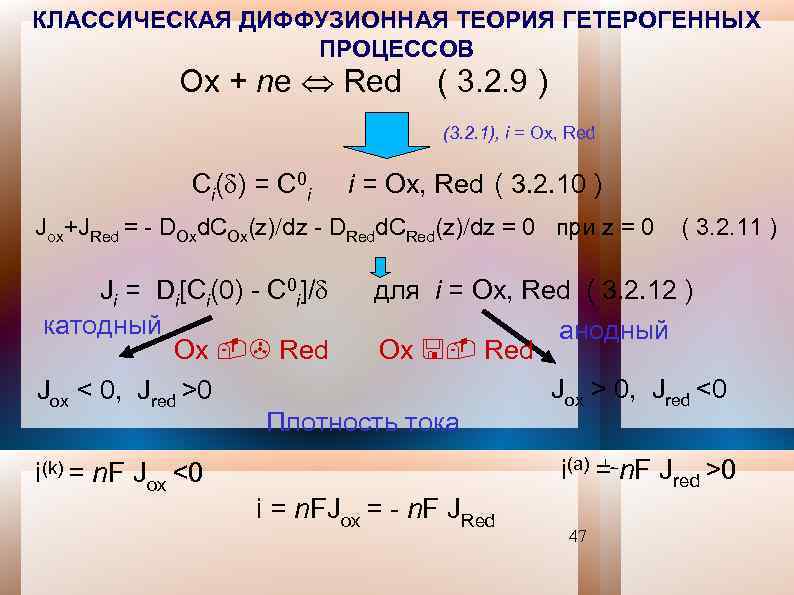КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ Ox + ne Red ( 3. 2. 9 ) (3. 2. 1), i = Ox, Red Ci( ) = C 0 i i = Ox, Red ( 3. 2. 10 ) Jox+JRed = - DOxd. COx(z) dz - DRedd. CRed(z) dz = 0 при z = 0 ( 3. 2. 11 ) Ji = Di[Ci(0) - C 0 i]/ для i = Ox, Red ( 3. 2. 12 ) катодный анодный Ox -> Red Ox <- Red Jox > 0, Jred <0 Jox < 0, Jred >0 Плотность тока i(k) = n. F Jox <0 i(a) = n. F Jred >0 i = n. FJox = - n. F JRed 47

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ Ji = Di[Ci(0) - C 0 i]/ для i = Ox, Red ( 3. 2. 12 ) Из 3. 2. 12 выразим COx(0)=C 0 Ох[1+JOx /DOx. C 0 Ох]; CRed(0)=C 0 Red[1 -JOx /DRed. C 0 Red] ( 3. 2. 14 ) Уравнение Нернста Е = Е 0 (RT/n. F)ln CRed(0)/COx(0) ( 3. 2. 13 ) (3. 2. 14) Е = Е 0 (RT/n. F){ln. C 0 Red/C 0 Ох + ln[1 - JOx /DRed. C 0 Red]/[1+JOx /DOx. C 0 Ох]} ( 3. 2. 15 ) Ji = i/n. F Е = Е 0 (RT/n. F){ln. C 0 Red/C 0 Ох + ln[1 - i /n. FDRed. C 0 Red]/[1+ i /n. FDOx. C 0 Ох]} ( 3. 2. 16 ) 48

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ Ji = Di[Ci(0) - C 0 i]/ для i = Ox, Red ( 3. 2. 12 ) i = n. FJox = - n. F JRed ik = n. FDox[Cox(0) - C 0 i]/ ia = -n. FDred[Cred(0) - C 0 i]/ Предельное значение (Ci(0) = 0) i(k)lim = - n. FDOx. C 0 Ох/ ( 3. 2. 17 а ) i(a)lim = n. FDRed. C 0 Red/ ( 3. 2. 17 б ) 49

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ i(k)lim < 0 i(k)lim = - n. FDOx. C 0 Ох/ ( 3. 2. 17 а ) i(a)lim > 0 i(a)lim = n. FDRed. C 0 Red/ ( 3. 2. 17 б ) = - n. FDOx. C 0 Ох/ i(k)lim ( 3. 2. 17 в ) = n. FDRed. C 0 Red/ i(a)lim ( 3. 2. 17 г ) ik = n. FDox[Cox(0) - C 0 i]/ ia = -n. FDred[Cred(0) - C 0 i]/ COx(0) = C 0 Ох [1 - i/i(k)lim], CRed(0) = C 0 Red[1 - i/i(a)lim] ( 3. 2. 18 ) Подставив в 3. 2. 16, получим Е = Е 0 (RT/n. F){ln. C 0 Red/C 0 Ох+ln[1 - i/i(a)lim]/[1 - i/i(k)lim]} ( 3. 2. 1 ) 50 I/I(k)lim I/I(a)lim

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ в условиях отсутствия продуктов реакции в объеме раствора: C 0 Red= 0 (катодный процесс) либо C 0 Ох= 0 (анодный процесс) COx(0)=C 0 Ох[1+JOx /DOx. C 0 Ох] CRed(0)=C 0 Red[1 -JOx /DRed. C 0 Red] ( 3. 2. 14 ) кат ан COx(0)=C 0 Ох[1+JOx /DOx. C 0 Ох] CRed(0)=-JOx /DRed COx(0)=JOx /Dox CRed(0)=C 0 Red[1 JOx /DRed. C 0 Red] Е = Е 0 (RT/n. F)ln CRed(0)/COx(0) ( 3. 2. 13 ) кат = - n. FDOx. C 0 Ох/ i(k)lim ( 3. 2. 17 в ) = n. FDRed C 0 ан (a) Red/ i lim ( 3. 2. 17 г ) Ji = i/n. F Е = Е 0 (RT/n. F){ln. DRed/Dox+ + ln i/(i(k)lim - i)} ( II. 2. 19 a ) Е = Е 0+(RT/n. F){ln. DRed/Dox+ + ln i/(i(a)lim - i)} ( II. 2. 19 б ) 51

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ: практическое применение Катодный: Анодный: 52

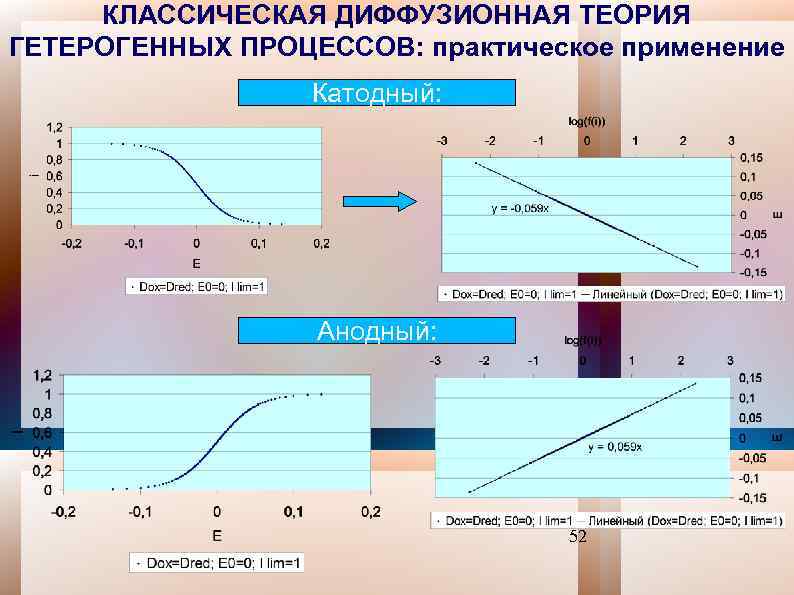
КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ: практическое применение Катодный: Е = Е 0 (RT/n. F){ln. DRed/Dox+ + ln i/(i(k)lim - i)} ( II. 2. 19 a ) Анодный Е = Е 0+(RT/n. F){ln. DRed/Dox+ + ln i/(i(a)lim - i)} ( II. 2. 19 б ) Е от log f(j), где f(j) = j/(j(k)lim - j) для катодного процесса и f(j) = j/(j(а)lim - j) в случае анодного, тогда tg = lg f(j) = 2, 303 RT/n. F 59 м. В/n. Обнаружение на опыте таких углов наклона поляризационных кривых - один из критериев обратимости исследуемого электродного процесса. 53

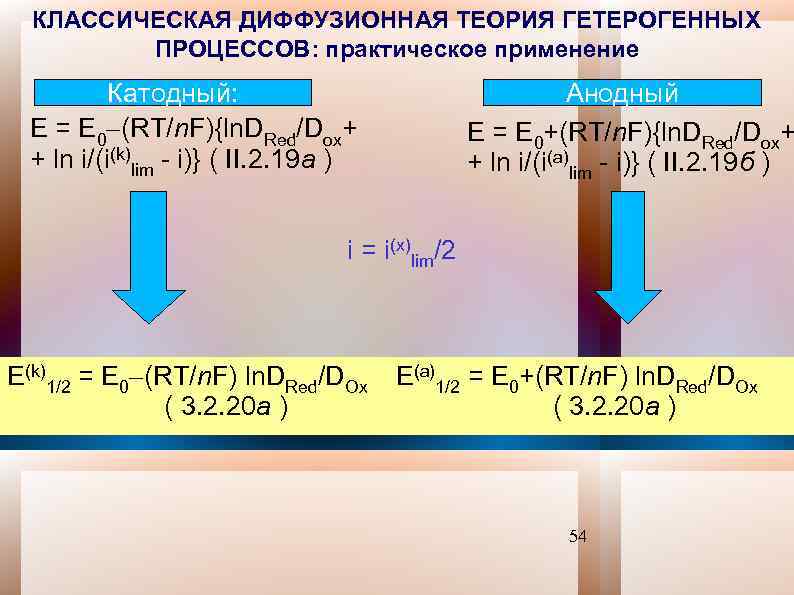КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ: практическое применение Катодный: Е = Е 0 (RT/n. F){ln. DRed/Dox+ + ln i/(i(k)lim - i)} ( II. 2. 19 a ) Анодный Е = Е 0+(RT/n. F){ln. DRed/Dox+ + ln i/(i(a)lim - i)} ( II. 2. 19 б ) i = i(x)lim/2 Е(k)1/2 = Е 0 (RT/n. F) ln. DRed/DOx Е(a)1/2 = Е 0+(RT/n. F) ln. DRed/DOx ( 3. 2. 20 а ) 54

КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ ГЕТЕРОГЕННЫХ ПРОЦЕССОВ: практическое применение КЛАССИЧЕСКАЯ ДИФФУЗИОННАЯ ТЕОРИЯ Конечность скорости гетерогенных процессов – предельные токи Потенциал полуволны – качественная характеристика системы Определение концентраций из предельного тока Идентификация компонентов смеси 55

Отклонения от классической теории: миграция 0. Избыток фонового электролита i( )/n. F = - Did. Ci/dz 1. Бинарный электролит с катионами K и анионами А зарядностей z 1 и - z 2, соответственно; Kz 1+z 1 е K(0) i(1)/z 1 F = - (1+z 1/z 2)D 1 d. C 1/dz; jlim(1) = (1+z 1/z 2) jlim( ) = - (1+z 1/z 2)z 1 F D 1 C 01/ Допущение: условие локальной электронейтральности: z 1 С 1 = z 2 С 2 для всех z из (0, ) 56

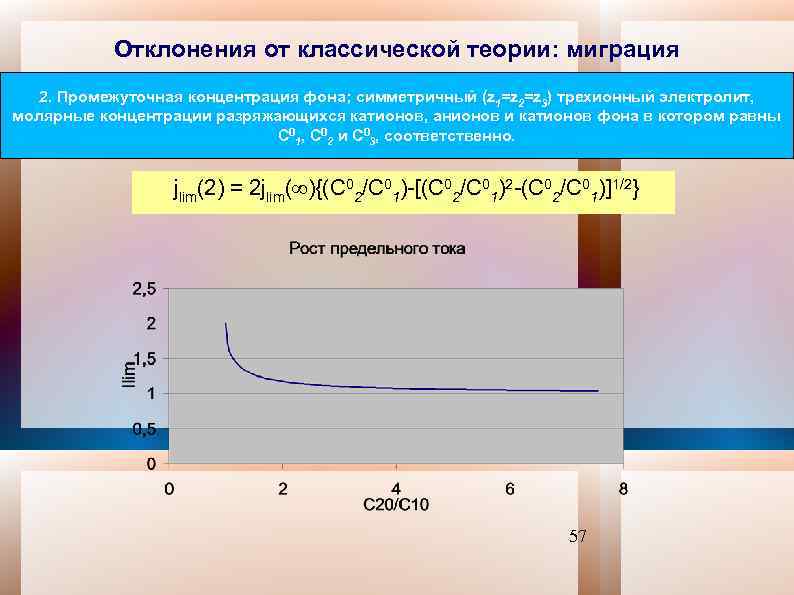Отклонения от классической теории: миграция 2. Промежуточная концентрация фона; симметричный (z 1=z 2=z 3) трехионный электролит, молярные концентрации разряжающихся катионов, анионов и катионов фона в котором равны C 01, C 02 и C 03, соответственно. jlim(2) = 2 jlim( ){(C 02/C 01)-[(C 02/C 01)2 -(C 02/C 01)]1/2} 57

Отклонения от классической теории: миграция 3. Сложный случай K z 1+z 0 е K z 1 - z 0 с z 0 z 1 на примере S 2 O 8 -2 + 2 e 2 SO 4 -2 в смеси K 2 S 2 O 8 и K 2 SO 4 C 02/2 C 01 = 1 ilim(3) = 3 ilim( ){[(2 D 1/D 3)1/3 - 1]/[(2 D 1/D 3) - 1]}= 3 ilim( )/[(2 D 1/D 3)2/3 + (2 D 1/D 3)1/3 + 1] В зависимости от того является ли отношение между коэффициентами диффузии D 1/D 3 восстанавливающихся (S 2 O 8 -2) и образующихся (SO 4 -2) на электроде анионов большим или меньшим 1/2, предельный ток в отсутствие фонового электролита, jlim(3), меньше или больше реализующегося в избытке фона, jlim( ), соответственно. Для рассматриваемого процесса ЭВ персульфат-ионов отношение этих токов должно составлять 0, 76, поскольку D 1/D 3 1, 08. Анализируя более общую ситуацию составов раствора C 02/2 C 01 > 1, можно установить, как и в предыдущем случае ЭВ катионов, что миграционные эффекты становятся заметными при сопоставимых концентрациях анионов S 2 O 8 -2 и катионов фона. 58