Основные гидродинамические понятия и законы Ламинарное и турбулентное

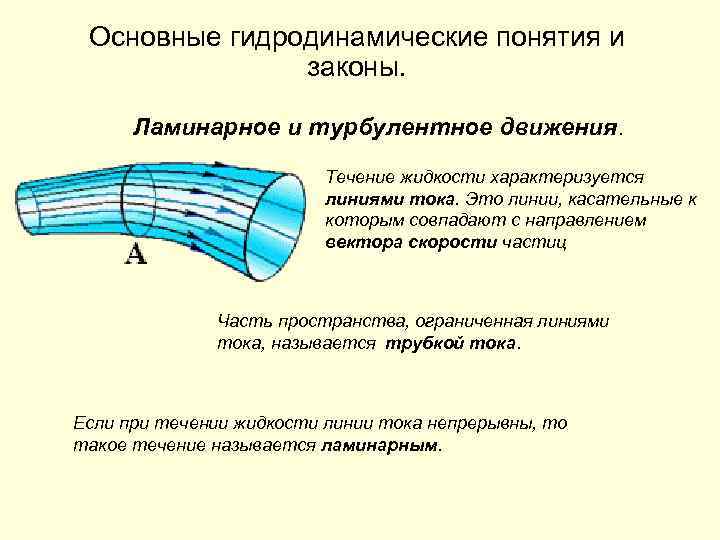
Основные гидродинамические понятия и законы. Ламинарное и турбулентное движения. Течение жидкости характеризуется линиями тока. Это линии, касательные к которым совпадают с направлением вектора скорости частиц Часть пространства, ограниченная линиями тока, называется трубкой тока. Если при течении жидкости линии тока непрерывны, то такое течение называется ламинарным.

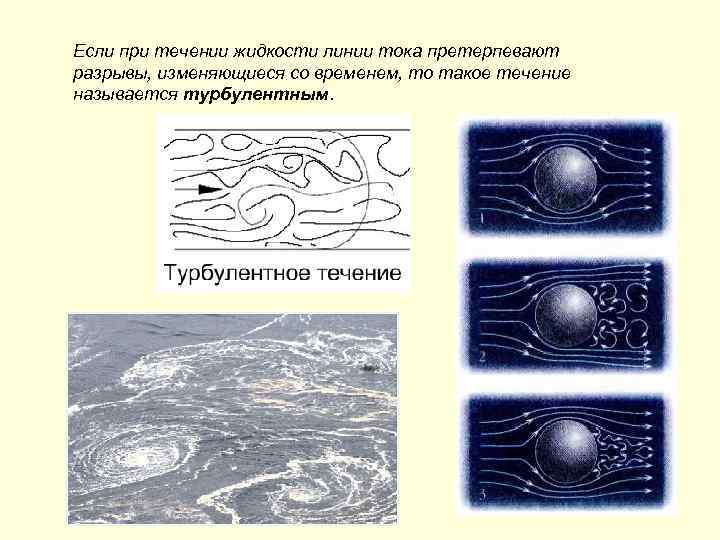
Если при течении жидкости линии тока претерпевают разрывы, изменяющиеся со временем, то такое течение называется турбулентным.

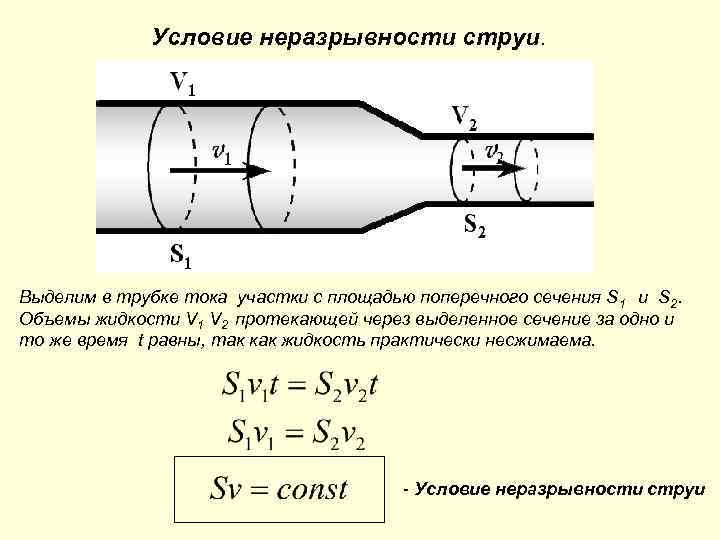
Условие неразрывности струи. Выделим в трубке тока участки с площадью поперечного сечения S 1 и S 2. Объемы жидкости V 1 V 2 протекающей через выделенное сечение за одно и то же время t равны, так как жидкость практически несжимаема. - Условие неразрывности струи

При течении жидкости различают линейную и объёмную скорости движения. Линейная скорость, путь проходимый частицами жидкости в единицу времени. Объемная скорость – это объём жидкости V, протекающий через некоторое сечение за единицу времени. Условие неразрывности выполняется и в реальной гемодинамике. В любом сечении сердечно - сосудистой системы объемная скорость кровотока одинакова Q = const. Оценки скоростей кровотока дают следующие значения: в аорте 0. 4 – 0. 5 м/с в капиллярах ≈ 0. 5 мм/с

Уравнение Бернулли. Рассмотрим трубку тока идеальной жидкости, в которой выделим два сечения с площадью S 1 и S 2. Пусть слои жидкостей расположены на высотах h 1 , h 2. Линейные скорости движения обозначим жидкости v 1 v 2. Силы, обусловливающие движение жидкости, оказывают давление P 1 P 2 на торцах. m – масса жидкости объёма V Разделим обе части уравнения на объём жидкости V :

- плотность жидкости - уравнение Бернулли Сумма разнопричинных давлений в любом сечении трубки тока (сосуда) является постоянной величиной - динамическое давление жидкости - статическое давление жидкости (не связанное с движением жидкости) - весовое (гидростатическое ) давление жидкости

Следствия, вытекающие из уравнения Бернулли. 1. Способ измерения скорости движения жидкости. Рассмотрим две трубки опущенные жидкость, одна прямая другая изогнутая Подъём жидкости в прямой трубке на высоту h 2 обусловлен лишь статическим давлением Pc = ρgh 2. В трубке Пито (изогнутая) подъём жидкости обусловлен суммой статического и динамического давлений.

2. Всасывающее действие струи. Рассмотрим течение жидкости по горизонтальной трубе переменного сечения. И пусть S 1 > S 2 и пусть h 1 = h 2. Давление жидкости в широкой области выше, чем в узких местах. Если сужение значительно, то статическое давление резко убывает и может быть ниже атмосферного. В этом случае воздух будет засасываться через отверстие в месте расположения сужения. На этом принципе устроены водоструйные насосы, ингаляторы, пульверизаторы.

3. Закупорка артерии, артериальный шум. В случае возникновения атеросклеротической бляшки на некотором участке артерии диаметром d 1 может возникнуть сужение диаметром d 2. Согласно уравнению Бернулли : d 1 (атмосферное) P 1 d 2 P 2 Течение крови по артерии будет происходить до тех пор, статическое давление в области атеросклеротической бляшки P 2 больше атмосферного : Это условие будет реализовано, когда пока диаметр сужения d 2 превышает либо равен некоторому минимальному значению dmin Например, для сонной артерии d 1 =1 см при скорости крови 0. 2 м/с и плотности крови ρ=1. 05*103 кг/м 3 разность давлений будет 100 мм рт. ст. Расчет дает минимальное значение диаметра просвета сосуда dmin ≈ 2 мм

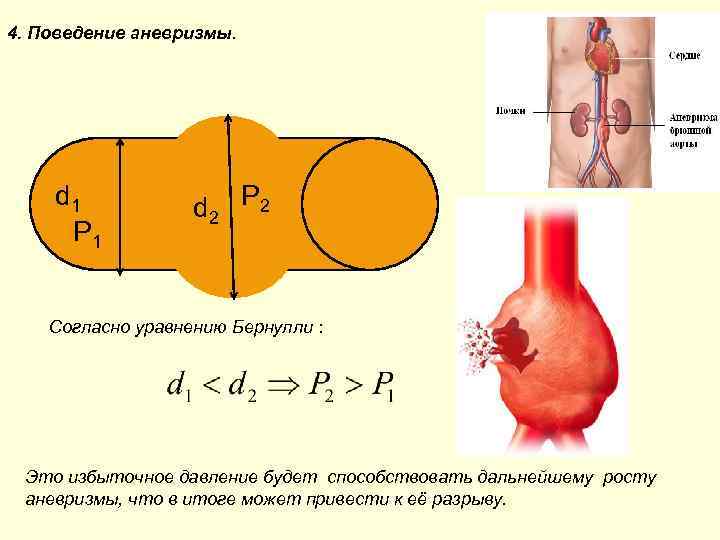
4. Поведение аневризмы. d 1 P 1 d 2 P 2 Согласно уравнению Бернулли : Это избыточное давление будет способствовать дальнейшему росту аневризмы, что в итоге может привести к её разрыву.

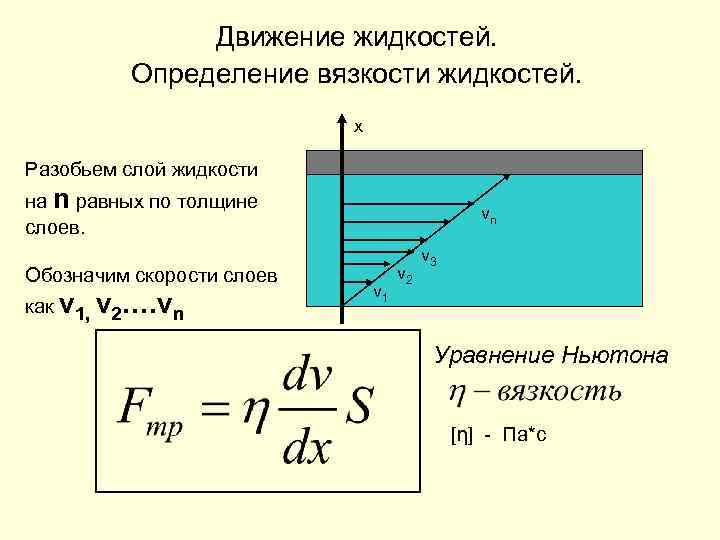
Движение жидкостей. Определение вязкости жидкостей. x Разобьем слой жидкости на n равных по толщине слоев. Обозначим скорости слоев как v 1, v 2…. vn vn v 1 v 2 v 3 Уравнение Ньютона [η] - Па*с

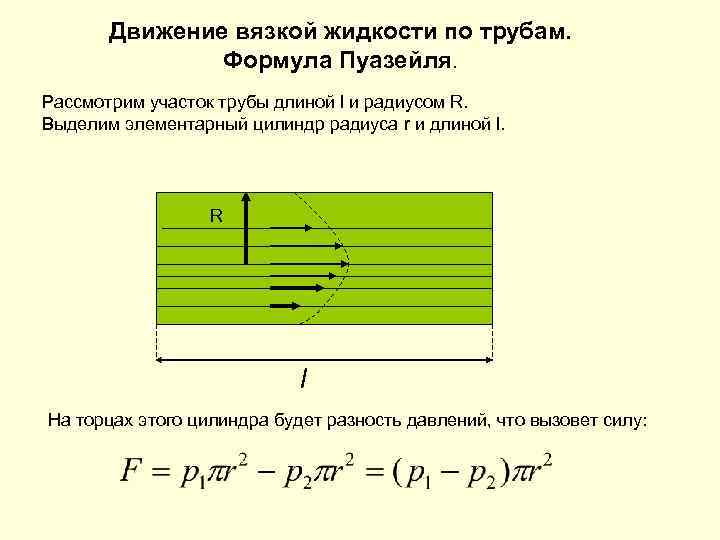
Движение вязкой жидкости по трубам. Формула Пуазейля. Рассмотрим участок трубы длиной l и радиусом R. Выделим элементарный цилиндр радиуса r и длиной l. R l На торцах этого цилиндра будет разность давлений, что вызовет силу:

На боковую поверхность будет действовать сила трения: Так как жидкость движется равномерно, то силы F и Fтр должны уравновесить друга: Проинтегрируем это уравнение:

Имеется параболическая зависимость скорости движения жидкости от расстояния. Слои в центре будут иметь максимальную скорость, слои около стенок сосуда минимальную. Определим теперь, от каких факторов зависит объем жидкости, прошедший через трубу за 1 с. Выделим цилиндрический слой длиной l и радиусом dr: Интегрируя по всему сечению, найдем:

Формула Пуазейля Количество вещ-ва прошедшее через цилиндр будет тем больше, чем больше радиус цилиндра и чем меньше вязкость. Аналогия между законом Ома и ф-лой Пуазейля I Q Cила тока, объем ж-ти U P 1 – P 2 Напряжение, раз-ть дав. I R X Сопротивление

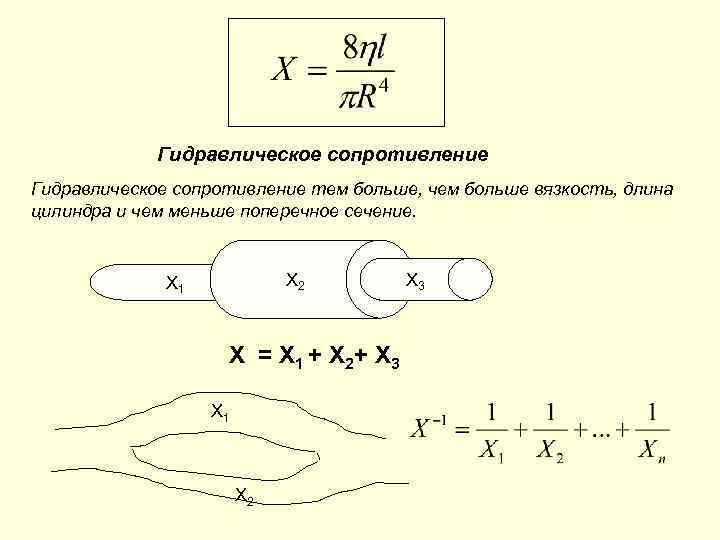
Гидравлическое сопротивление тем больше, чем больше вязкость, длина цилиндра и чем меньше поперечное сечение. X 2 X 1 X = X 1 + X 2+ X 3 X 1 X 2 X 3

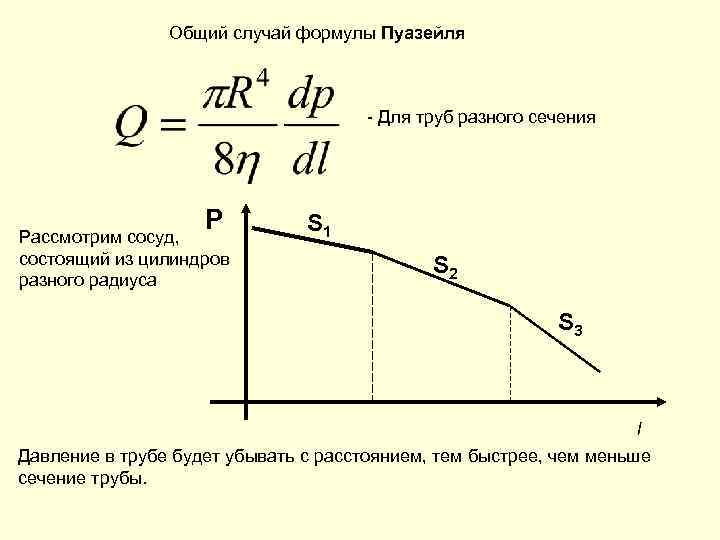
Общий случай формулы Пуазейля - Для труб разного сечения P Рассмотрим сосуд, состоящий из цилиндров разного радиуса S 1 S 2 S 3 l Давление в трубе будет убывать с расстоянием, тем быстрее, чем меньше сечение трубы.

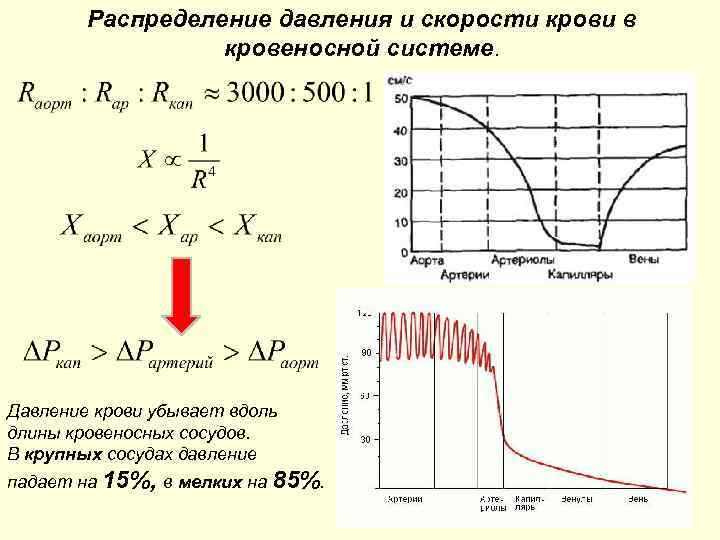
Распределение давления и скорости крови в кровеносной системе. Давление крови убывает вдоль длины кровеносных сосудов. В крупных сосудах давление падает на 15%, в мелких на 85%.

Условия перехода ламинарного течения жидкости в турбулентное. - движение жидкости будет ламинарным - движение жидкости будет турбулентным Для гладких труб и ньютоновской жидкости Re =2300 Для крови Re = 900 -1600

Движение тел в вязкой жидкости. Закон Стокса. Расмотрим тело, движущееся в вязкой жидкости. На тело действуют силы: Сила тяжести F = mg Cила Архимеда Fa =ρжg. Vт Сила трения Fтр = 6π ηrv

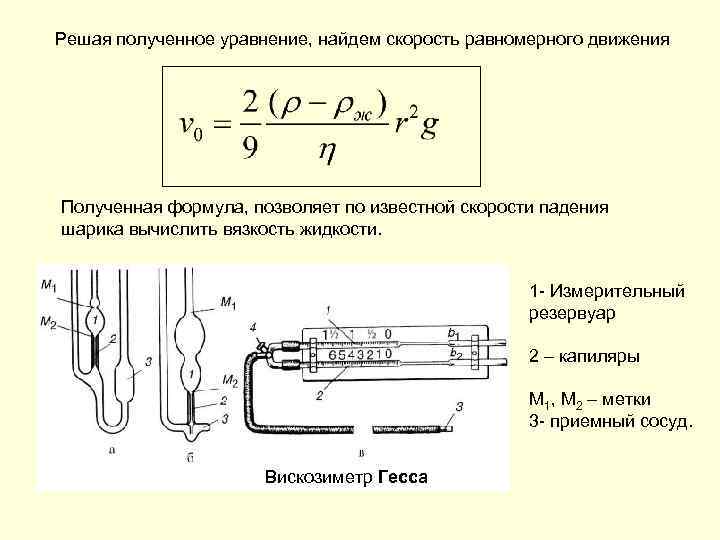
Решая полученное уравнение, найдем скорость равномерного движения Полученная формула, позволяет по известной скорости падения шарика вычислить вязкость жидкости. 1 - Измерительный резервуар 2 – капиляры М 1, М 2 – метки 3 - приемный сосуд. Вискозиметр Гесса

Ротационный вискозиметр

Некоторые особенности движения крови по сосудам. Движение крови в организме в основном ламинарное, однако при определенных условиях кровоток может приобретать и турбулентный характер. Турбулентность может возникать : - В полостях сердца ( возникшие завихрения приводят к перемешиванию крови) -Небольшие завихрения могут возникать вблизи клапанов сердца -При интенсивной физической нагрузке (увеличивается скорость и может возникнуть турбулентное движение) - При атеросклеротических бляшках в сосудах (небольшой просвет Приводит к увеличению скорости и как результат возникновению турбулентности)

Факторы, влияющие на вязкость крови в живом организме. 1. Температура. При повышении температуры вязкость крови падает. В переохлажденных участках организма вязкость увеличивается, кровоток затрудняется, ухудшается питание тканей, что приводит к развитию патологических процессов. 2. Гематокрит. Этот показатель представляет собой отношение объема эритроцитов к объёму крови. В норме : C повышением гематокрита вязкость крови возрастает. Это может быть связано как с повышением концентрации эритроцитов, их агрегации, так и за счет увеличения их размеров.

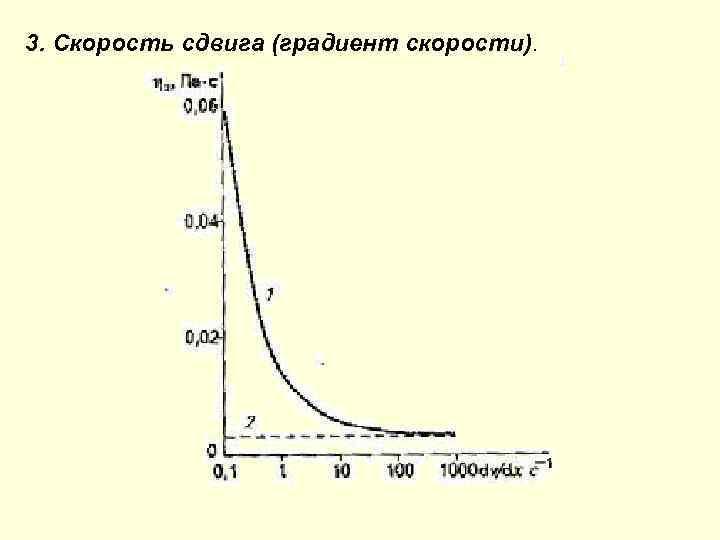
3. Скорость сдвига (градиент скорости).

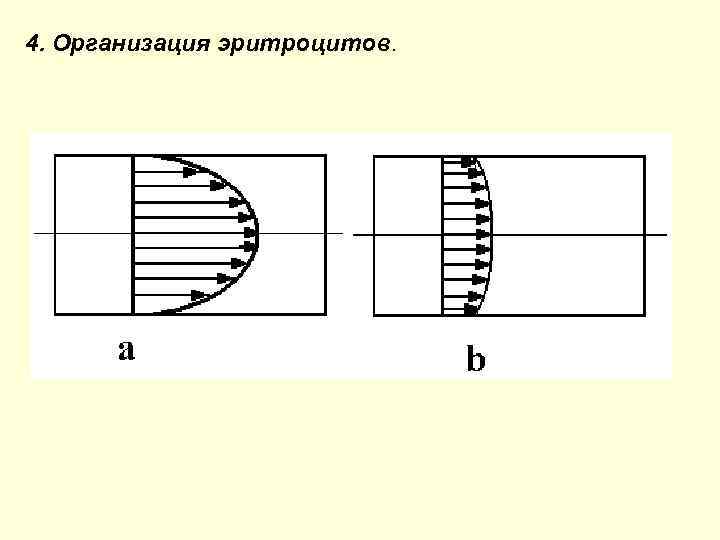
4. Организация эритроцитов.