c68cbb04447b69fd56f8f7527bbb8e4d.ppt
- Количество слайдов: 19

Основная задача линейного программирования Симплекс-метод

Симплекс-таблица n n n Теперь мы в состоянии сформулировать алгоритм симплексметода для решения задач линейного программирования, заданных в канонической форме. Обычно он реализуется в виде так называемой симплекс-таблицы. В первом столбце этой таблицы располагаются обозначения переменных, входящих в базис. Второй столбец - коэффициенты целевой функции, соответствующие переменным, входящим в базис. Третий столбец - компоненты опорного плана. В дополнительной строке в этом столбце пишется величина Её легко вычислить перемножая числа из второго столбца и третьего столбца и складывая их.

Симплекс-таблица n n n Далее идут столбцы, соответствующие всем переменным, и в этих столбцах записываются координаты этих переменных в рассматриваемом базисе. Заметим, что для базисных переменных эти координаты имеют вид (0, 0, . . . , 0, 1, 0, . . . , 0), где единица стоит в той строке, где находится этота базисная переменная. В дополнительной строке сверху обычно выписывают коэффициенты , соответствующие этим переменным в целевой функции. В дополнительной строке снизу пишутся величины , вычисляемые по формулам:

Симплекс-таблица n n Заметим, что для векторов, входящих в базис, эти разности всегда равны нулю. Далее идут следующие этапы, связанные с преобразованием этой таблицы. При ручном счете каждый раз эту таблицу лучше переписывать заново, при счете на ЭВМ (который, естественно, всегда используется при решении практических, а не учебных задач), эта таблица просто преобразуется в памяти ЭВМ.

Этап 1 n Просматривается дополнительная строка снизу, где записаны разности. Если все эти разности меньше, либо равны нулю, то план является оптимальным

Этап 2 n n Если есть столбцы, где в нижней строке есть величина больше нуля, то выбирается столбец с максимальным значением этой величины. Индекс j определит вектор, вводимый в базис. Пусть max(zj-cj)=zl-cl, то есть в базис надо вводить переменную xl. Назовем столбец, соответствующий этой переменной, направляющим столбцом. В дальнейшем мы будем направляющий столбец помечать символом ⇒.

Этап 3 n n Просматривается направляющий столбец. Если все ail<0, то значения целевой функции неограничены снизу. Если есть ail>0, то находится min(i)(xi/ail), где просматриваются лишь те дроби, для которых ail>0. Пусть этот минимум достигается для akl. Тогда именно переменная xk подлежит выводу из базиса. Строка, соответствующая этой переменной, называется направляющей строкой. В дальнейшем в примерах мы будем помечать ее символом ⇑.

Этап 4 n n После того, как определены направляющие столбец и строка, начинает заполняться новая симплекстаблица, в которой на месте направляющей строки будет стоять переменная xl. Обычно заполнение этой новой таблицы начинается именно с направляющей строки. В качестве компоненты опорного плана туда пишется величина xk/akl. Остальные элементы этой строки заполняются величинами a’lj=akj/akl.

Этап 4 n n Обратите внимание на особую роль элемента akl, стоящего на пересечении направляющей строки и направляющего столбца. Именно на него делятся все бывшие элементы направляющей строки. На месте бывшего элемента автоматически появляется единица. Написанные выше формулы для пересчета элементов направляющей строки можно записать следующим правилом: akl

Этап 5 n Далее начинается пересчет всех остальных строк таблицы, включая и дополнительную нижнюю строку для компонент плана; для координат разложения по базису; для дополнительной строки по следующему правилу n Далее итерации продолжаются.

Пример n Решить задачу линейного программирования
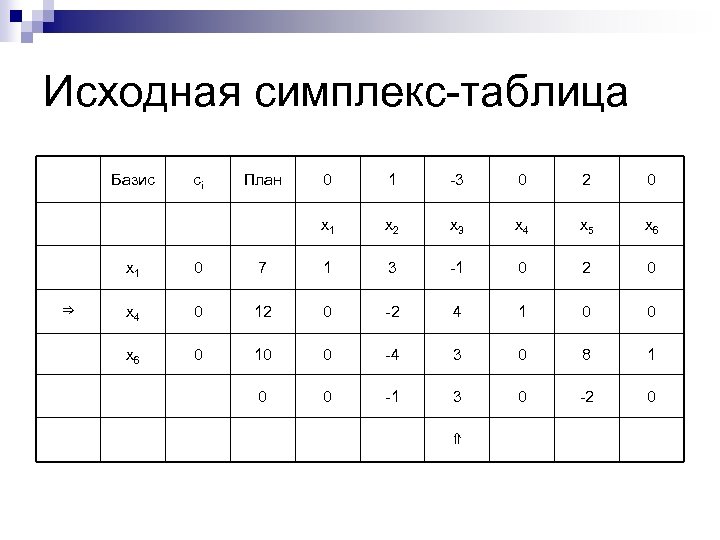
Исходная симплекс-таблица Базис сi План 0 1 -3 0 2 0 x 1 x 2 x 3 x 4 x 5 x 6 x 1 ⇒ 0 7 1 3 -1 0 2 0 x 4 0 12 0 -2 4 1 0 0 x 6 0 10 0 -4 3 0 8 1 0 0 -1 3 0 -2 0 ⇑

Пример n n Обратите внимание на то, что из-за специфического вида системы ограничений в столбец "план" просто переписался вектор свободных членов системы ограничений. Ну, а величины z 0 и zj-cj приходится считать:

Первая итерация n n Просматривая дополнительную строку мы видим, что в ней всего один положительный элемент в столбце, соответствующем переменной x 3. Следовательно, эту переменную надо вводить в базис и этот столбец и будет направляющим столбцом. В этом направляющем столбце есть два положительных числа 4 и 3. Поэтому нужно рассмотреть два частных 12/4 и 10/3 и выбрать из них наименьшее. Так как min ((12/4), (10/3))=3 и он достигается на a 43=4 , то этот вектор подлежит выводу из базиса и соответствующая ему строка и будет направляющей строкой. Заполним теперь новую симплекс-таблицу, следуя сформулированным выше правилам. Начинается заполнение, естественно, со второй строки (так как она была направляющей), а затем пересчитываются все остальные строки.

Полученная симплекс-таблица Базис План 0 1 -3 0 2 0 x 1 ⇒ сi x 2 x 3 x 4 x 5 x 6 x 1 0 10 1 5/2 0 1/4 2 0 x 3 -3 3 0 -1/2 1 1/4 0 0 x 6 0 1 0 -5/2 0 -3/4 8 1 -9 0 1/2 0 -3/4 -2 0 ⇑

Вторая итерация n n Просматривая дополнительную строку мы вновь видим в ней всего один положительный элемент это 1/2, стоящая в столбце x 2. Следовательно, этот вектор надо ввести в базис и этот столбец будет направляющим. В столбце, соответствующем x 2, всего один положительный элемент это 5/2 в первой строке. Поэтому первая строка будет направляющей и переменная x 1 должна быть выведена из базиса.
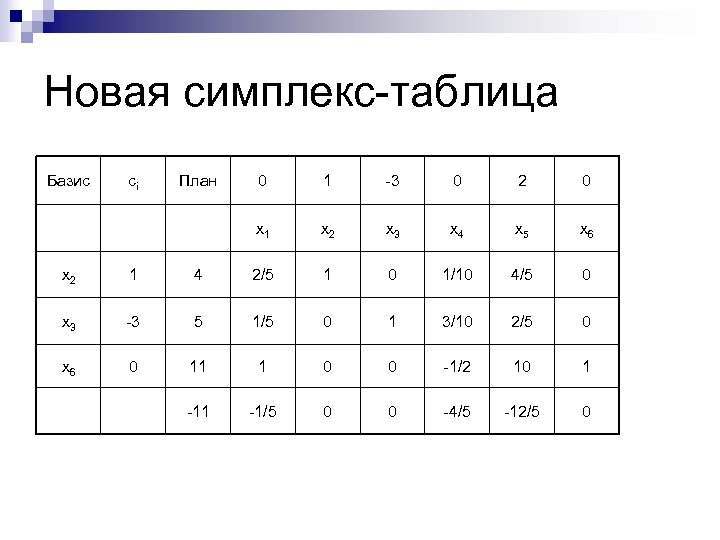
Новая симплекс-таблица Базис сi План 0 1 -3 0 2 0 x 1 x 2 x 3 x 4 x 5 x 6 x 2 1 4 2/5 1 0 1/10 4/5 0 x 3 -3 5 1/5 0 1 3/10 2/5 0 x 6 0 11 1 0 0 -1/2 10 1 -1/5 0 0 -4/5 -12/5 0

Решить

Решить
c68cbb04447b69fd56f8f7527bbb8e4d.ppt