ОСНОВИ ТЕОРІЇ ПЕРЕДАЧІ ІНФОРМАЦІЇ Лекція 13 КУТОВА МОДУЛЯЦІЯ

ОСНОВИ ТЕОРІЇ ПЕРЕДАЧІ ІНФОРМАЦІЇ Лекція 13. КУТОВА МОДУЛЯЦІЯ

Кутова модуляція – це загальна назва двох тісно пов’язаних між собою видів модуляції – частотної (ЧМ) і фазової (ФМ). У системах із частотною модуляцією інформація передається зміною миттєвої частоти несучого коливання, а при фазовій модуляції сигнал, що модулює, змінює безпосередньо фазу несучого коливання. Розглянемодульоване несуче коливання: . Повна фаза , – постійна початкова фаза. При кутовій модуляції: , де функція несе передане повідомлення. При модульоване коливання: .

Кутова модуляція При фазовій модуляції (ФМ) сигнал, що модулює, безпосередньо змінює фазу несучої, тобто зміна фази дорівнює: , де – деякий коефіцієнт. Тоді вираз для ФМ коливання має вигляд: . Для вивчення властивостей кутової модуляції корисно використати поняття миттєвої частоти , що визначається за формулами: , тобто миттєва кутова частота – це швидкість зміни повної фази.

Кутова модуляція При , миттєвої частоти відносно . При частотній модуляції (ЧМ) відхилення пропорційні сигналу, що модулює: , де – коефіцієнт, що має розмірність Гц/В. Звідси видно, що у випадку ЧМ миттєва початкова фаза дорівнює: . Вираз для ЧМ коливання має вигляд: .

Кутова модуляція Введемо характеристики кутової модуляції: індекс модуляції й девіацію частоти. Індексом модуляції називається максимальне відхилення фази несучого коливання: . Для ФМ сигналу: . При частотній модуляції відхилення миттєвої частоти від несучої дорівнює: , де – нормоване відхилення частоти; – девіація частоти несучої.

Кутова модуляція Розглянемо окремий випадок гармонійного коливання, що модулює: . У цьому випадку: . Модульований сигнал має вигляд: де – індекс модуляції при ЧМ.

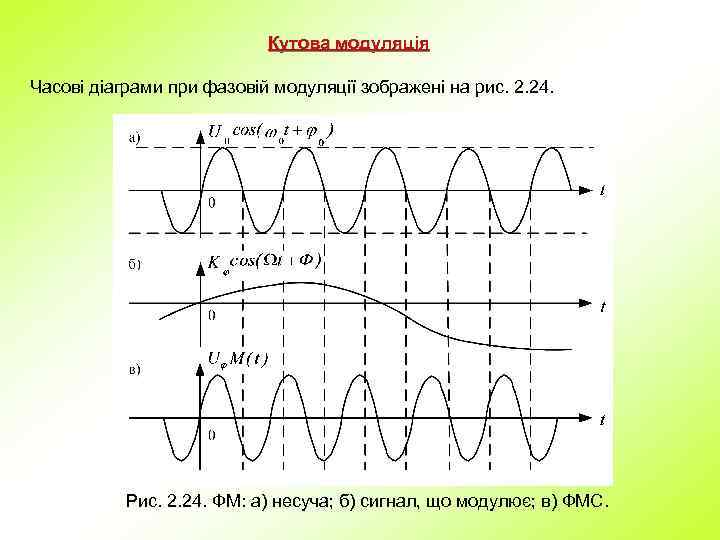Кутова модуляція Часові діаграми при фазовій модуляції зображені на рис. 2. 24. Рис. 2. 24. ФМ: а) несуча; б) сигнал, що модулює; в) ФМС.

Кутова модуляція Спектр при кутовій модуляції значно складніший спектра при AM. У найпростішому випадку гармонійного коливання, що модулює, справедливе розкладання модульованого коливання на наступну суму гармонік: де При ФМ – функція Бесселя n -го порядку аргументу. При ЧМ . .

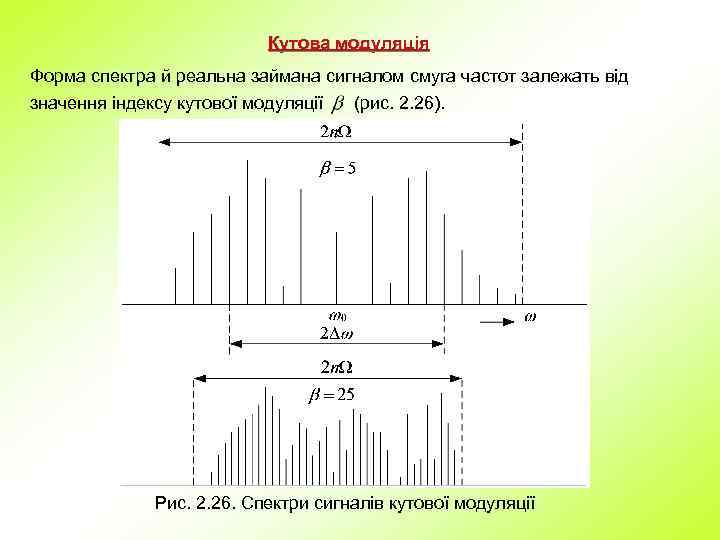Кутова модуляція Форма спектра й реальна займана сигналом смуга частот залежать від значення індексу кутової модуляції (рис. 2. 26). Рис. 2. 26. Спектри сигналів кутової модуляції