Основания Языков программирования Введение в Лямбда-исчисление На основе

Основания Языков программирования: Введение в Лямбда-исчисление На основе лекций профессров Айкена и Некюла университет Беркли 1

План • Зачем изучать лямбда-исчисление? • Лямбда-исчисление – Нотация – Вычисления – Связь с языками программирования 2

История создания • Предложено 1930 -ых Алонсо Черчем для изучения вычисления функций • Черч рассмотрел минимальную нотацию – Только ключевые понятия • Две операции являются ключевыми: – Объявление функции – Вычисление функции 3

Объявление функции • Черч предложил нотацию lx. E для обозначения функции с формальным аргументом x и телом E • У функций нет имен – Имена не требуются для вычисления • Функции имеют единственный аргумент – Функции нескольких аргументов являются простым обобщением без изменения нотации. 4

История нотации • 5

Применение функции к аргументу • Единственное действие над функцией – применение ее к аргументу • Черч использовал нотацию E 1 E 2 для обозначения применения функции E 1 к значению аргумента E 2 • Все функции применяются к единственному аргументу 6

Зачем изучать лямбда-исчисление? • l-исчисление оказывает гигантское влияние на разработку и анализ языков программирования • Реальные языки слишком велики и сложны для полного анализа • Типичный подход заключается в разбиении на отдельные свойства – рекурсия, циклы, исключения, объекты, итд. • Которые затем собираются вместе 7

Зачем изучать лямбда-исчисление? • l-исчисление – стандартная нотация для изучения различных свойств языков программирования • Из-за своей минимальности – Несмотря на простоту может кодировать: • числа, рекурсивные типы данных, модули, императивный порядок вычислений, исключения, итд. • Некоторые свойства языков требуют расширения нотации: – Для распределенных вычислений: p-исчисление – Для ООП: -исчисление 8

Зачем изучать лямбда-исчисление? “Неизвестно какими будут следующие 700 языков программирования, но они точно будут основаны на лямбда-исчислении. ” (Ландин 1966) 9

Нотация • Только 3 типа выражений E : : = x | E 1 E 2 | lx. E переменные применение функции к аргументу декларация функции • lx. E также называется лямбда абстракцией, или абстракцией • E 1 E 2 называется аппликацией • E называется l-терм или l-выражение 10

Примеры лямбда нотации • Тождественная функция: I =def lx. x • Функция, отбрасывающая аргумент y и вычисляющая тождественную функцию: ly. (lx. x) • Функция, применяющая функцию f к тождественной функции lf. f (l x. x) 11

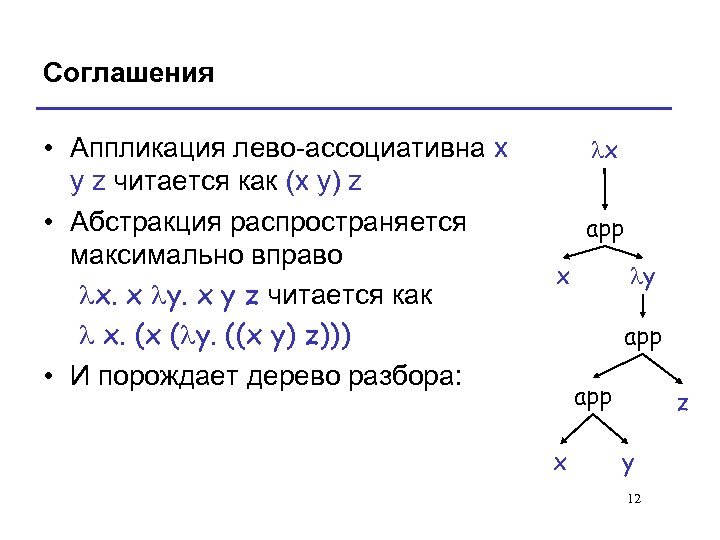
Соглашения • Аппликация лево-ассоциативна x y z читается как (x y) z • Абстракция распространяется максимально вправо lx. x ly. x y z читается как l x. (x (ly. ((x y) z))) • И порождает дерево разбора: lx app x ly app x z y 12

Области видимости переменных • Во всех языках с переменными важно определить область видимости (контекст) переменной, в которой она может использоваться в программе • Абстракция lx. E связывает переменную x в E – x – новая переменная – E – область видимости x – Мы говорим, что x – связанная переменная в lx. E – Также как формальный аргумент функции связан в теле функции 13

Свободные и связанные переменные • Мы говорим что переменная свободная в E, если она не связанная в E • Можно определить свободные переменные в E рекурсивно следующим образом: Free(x) = { x} Free(E 1 E 2) = Free(E 1) È Free(E 2) Free(lx. E) = Free(E) - { x } • Пример: Free(lx. x (ly. x y z)) = { z } • Свободные переменные декларируются вне выражения 14

Свободные и связанные переменные (2) • Как и в других языках со статическими вложенными контекстами мы должны заботиться о переопределении переменных – Использование переменной может ссылаться на различные значения в разных контекстах • Пример l-исчисление: lx. x (lx. x) x 15

Переименование связанных переменных • l-термы, которые могут быть получены друг из друга переименованием связанных переменных считаются идентичными • Пример: lx. x, ly. y, lz. z • Смысл: – При переименовании поведение функции не меняется – В l-исчислении функция определяется своим поведением 16

Переименование связанных переменных (2) • Соглашение: мы всегда переименовываем связанные переменные, чтобы они миели уникальные имена в выражении – пример, l x. x (l y. y) x вместо l x. x (l x. x) x • Это позволяет легче отследить область видимости переменных • И защищает от ошибок ! 17

Подстановка • Подстановка E’ вместо x в E (записывается [E’/x]E ) – 1. Переименовать связанные переменные в E и E’ чтобы имена стали уникальными – 2. Выполнить текстовую замену x на E’ в E • Пример: [y (lx. x) / x] ly. (lx. x) y x – После переименования: [y (lv. v)/x] lz. (lu. u) z x – После подстановки: lz. (lu. u) z (y (lv. v)) 18

Вычисление l-выражений • Ключевой шаг вычислений в l-исчислении: аппликация функций (lx. E) E’ вычисляется в [E’/x]E • Называется b-редукцией • E ®b E’ означает, что E’ получается из E за один шаг b-редукции • E ®*b E’ означает, что требуется 0 или более шагов 19

Примеры вычислений • Тождественная функция: (lx. x) E ® [E / x] x = E • Другой пример с тождественной функцией: (lf. f (lx. x)) (lx. x) ® [lx. x / f] f (lx. x)) = [(lx. x) / f] f (ly. y)) = (lx. x) (ly. y) ® [ly. y /x] x = ly. y • Бесконечные вычисления: (lx. xx) ® [lx. xx / x]xx = [ly. yy / x] xx = (ly. yy) ® … 20

Функции нескольких аргументов • Расширим исчисление при помощи примитивной операции add • lx. ly. add x y можно использовать для сложения аргументов E 1 and E 2: (lx. ly. add x y) E 1 E 2 ®b ([E 1/x] ly. add x y) E 2 = (ly. add E 1 y) E 2 ®b [E 2/y] add E 1 y = add E 1 E 2 • Аргументы передаются по одному 21

Функции нескольких аргументов (2) • Каков результат (lx. ly. add x y) E ? – ly. add E y (функция с аргументом y по значению E’ вычисляет add E E’) • Функция lx. ly. E примененная к E’ вычисляет функцию ly. [E’/x]E • Это – пример вычисления функций высшего порядка – Т. е. функций, возвращающих другую функцию 22

Вычисления и статическая область видимости • Определение подстановки гарантирует сохранение статического контекста: (l x. (ly. y x)) (y (lx. x)) ®b lz. z (y (lv. v)) (y остается свободной, т. е. определяется снаружи) • Если забыть переименовать связанную y: (l x. (ly. y x)) (y (lx. x)) ®*b ly. y (y (lv. v)) (y стала связанной) 23

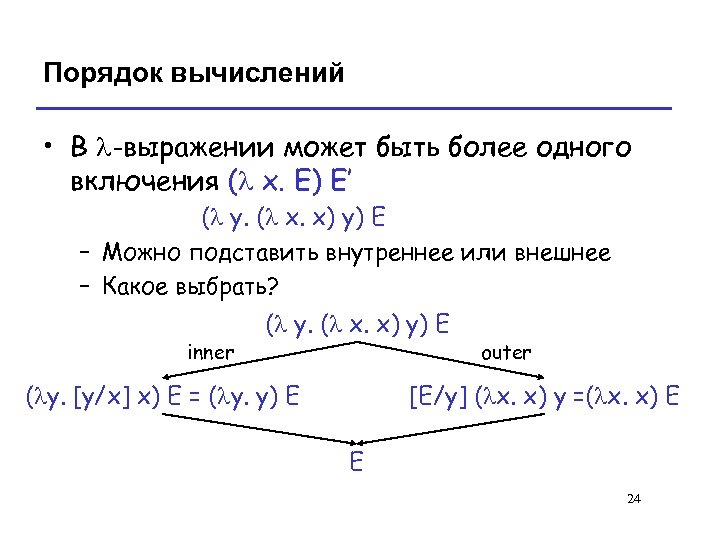
Порядок вычислений • В l-выражении может быть более одного включения (l x. E) E’ (l y. (l x. x) y) E – Можно подставить внутреннее или внешнее – Какое выбрать? inner (l y. (l x. x) y) E (ly. [y/x] x) E = (ly. y) E outer [E/y] (lx. x) y =(lx. x) E E 24

Порядок вычислений (2) • Теорема Черча-Россера утверждает, что если вычисление завершится, то результат будет одинаков – Результат – несократимое l-выражение • Для моделирования определенных языков мы нам может потребоваться зафиксировать порядок вычислений • В большинстве языков программирования мы не подставляем тела функций под l – Функции считаются значениями 25

Вызов по имени • Не вычислять под l • Не вычислять аргумент до вызова • Пример: (ly. (lx. x) y) ((lu. u) (lv. v)) ®bn (lx. x) ((lu. u) (lv. v)) ®bn (lu. u) (lv. v) ®bn lv. v 26

Вызов по значению • Не вычислять под l • Вычислять аргумент до вызова • Пример: (ly. (lx. x) y) ((lu. u) (lv. v)) ®bv (ly. (lx. x) y) (lv. v) ®bv (lx. x) (lv. v) ®bv lv. v 27

Сравнение вызова по имени и значению • CBN – Сложен в реализации – Порядок эффектов не определен • CBV: – Прост в реализации – Может не завершаться – Пример: (lx. l z. z) ((ly. yy) (lu. uu)) • CBN редко используется по умолчанию для всех вычислений кроме экспериментальных реализаций функциональных языков 28

Сравнение лямбда-исчисления и языков программирования • Чистый лямбда содержит только функции • Если нам нужны другие типы данных: булевский, числа, списки, итд. ? • Можно закодировать в l-исчислении • Общий подход: кодировать не значение, а его поведение! • Для каждого типа данных требуется описать его поведение в виде функции – Затем закодировать функцию в l-исчислении 29

Булевский тип • Что можно сделать с булевским значением? – Бинарный выбор • Булевский тип – функция выбирающая из двух альтернатив – true =def lx. ly. x – false =def lx. ly. y – if E 1 then E 2 else E 3 =def E 1 E 2 E 3 • Пример: если true то u иначе v (lx. ly. x) u v ®b (ly. u) v ®b u 30

Пары • Что можно сделать с парой? – Выбрать один из элементов • Пара – функция по булевскому значению выбирающая левый или правый элемент mkpair x y =def l b. x y fst p =def p true snd p =def p false • Пример: fst (mkpair x y) ® (mkpair x y) true ® true x y ® x 31

Натуральные числа • Что можно сделать с натуральным числом? – Итерировать функцию заданное число раз • Натуральное число – функция применяющая, функцию f рекурсивно с начальным значением s: 0 =def lf. ls. s 1 =def lf. ls. f s 2 =def lf. ls. f (f s) итд. 32

Вычисления с натуральными числами • Следующее число succ n =def lf. ls. f (n f s) • Сложение add n 1 n 2 =def n 1 succ n 2 • Умножение mult n 1 n 2 =def n 1 (add n 2) 0 • Сравнение с 0 iszero n =def n (lb. false) true 33

Вычисления с натуральными числами (2) mult 2 2 ® 2 (add 2) 0 ® (add 2) ((add 2) 0) ® 2 succ (add 2 0) ® 2 succ (2 succ 0) ® succ (succ 0))) ® succ (succ (lf. ls. f (0 f s)))) ® succ (succ (lf. ls. f s))) ® succ (lg. ly. g ((lf. ls. f s) g y))) succ (lg. ly. g (g y))) ®* lg. ly. g (g (g (g y))) = 4 34

Вычисления с натуральными числами (3) • Каков результат аппликации add 0 ? (ln 1. ln 2. n 1 succ n 2) 0 ®b ln 2. 0 succ n 2 = ln 2. (lf. ls. s) succ n 2 ®b ln 2. n 2 = lx. x • Вычисляя функции высших порядков мы можем исследовать различные оптимизации 35

Выразительность лямбда-исчисления • Можно выразить – – Типы данных (булевский, целый, списки, деревья, итд. ) Ветвления (используя булевский тип) Рекурсии Циклы • Этого достаточно для эмуляции машины Тюринга • Программирование в чистом l-исчислении громоздко и неудобно – Синтаксический сахар (0, 1, …, true, false, if-then-else, итд. ) – Типы данных с проверкой типов 36