Организация на компютъра Встъпително упражнение n n

Организация на компютъра Встъпително упражнение

n n n n Инструктаж по техника на безопасността Програма-конспект Учебник CD Уеб сайт на дисциплината - ecet. ecs. ru. acad. bg/else Общи указания за провеждане на упражненията Закъснения, отсъствия , проверки Контролни, курсова работа, изпит, освобождаване

Средна оценка от текущия контрол Отк ~ = 2 О кр + Ок 1 + Ок 2 4 Окр - оценка от курсовата работа Ок 1 и Ок 2 - оценки от двете контролни Предложение за освобождаване Отк > = 5 Желаещите да си повишат оценката могат да се явят на събеседване по целия материал!

Класификация на техническите системи по вида на информационния сигнал n Аналогови – сигналът се представя и обработва като непрекъсната функция във времето, която може да приема непрекъснати стойности по амплитуда; Примери: звукови вълни, телефонен апарат и др. n Импулсни – сигналът е дискретизиран (прекъснат, накъсан) във времето, но непрекъснат по амплитуда; Примери: релейни устройства, управление на класическа АТЦ и др. n Дискретни (Цифрови) – сигналът е дискретенизиран по време и по амлитуда, като на всяка дискрета може да се постави в съответствие цяло число.

Определения n Микрооперация – Това е най-елементарната машинна операция, която може да се изпълнява в машината (компютъра). n Бит – единица двоичен разряд “ 0” и “ 1”. n Байт – 8 бита. n Машинна дума – поредица от нули и единици с различна дължина – 8, 16, 32, 64, 128 разряда. Това може да бъде команда, данни, част от команда.

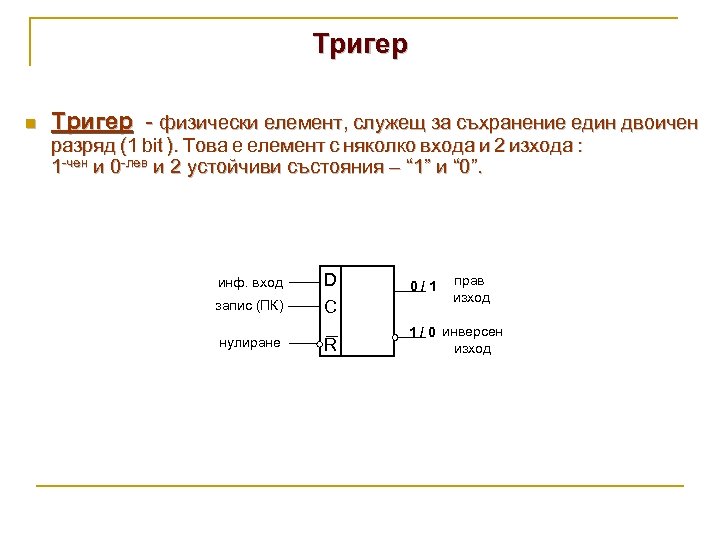Тригер n Тригер - физически елемент, служещ за съхранение един двоичен разряд (1 bit ). Това е елемент с няколко входа и 2 изхода : 1 -чен и 0 -лев и 2 устойчиви състояния – “ 1” и “ 0”. инф. вход запис (ПК) нулиране D C R 0/1 прав изход 1 / 0 инверсен изход

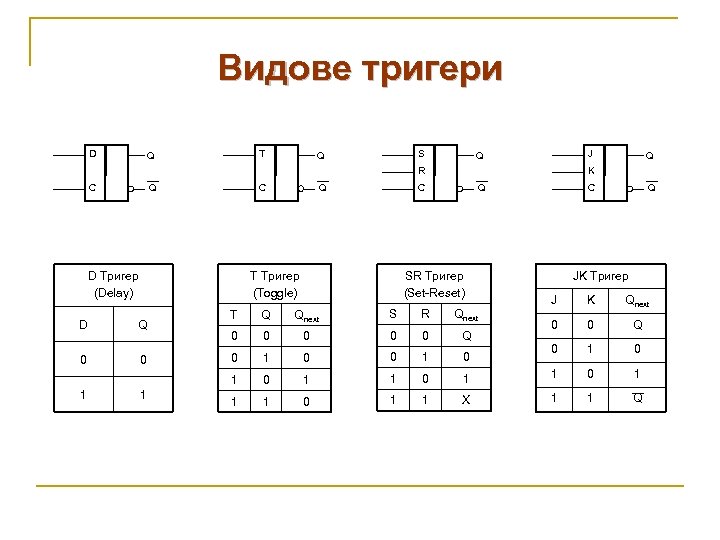Видове тригери D T Q S Q J Q R C C Q D Тригер (Delay) Q K Q C T Тригер (Toggle) SR Тригер (Set-Reset) Q 0 0 1 1 Q C JK Тригер J K Qnext 0 0 Q 0 1 1 0 1 X 1 1 Q T Q Qnext S R Qnext 0 0 0 Q 0 1 0 1 D Q 0 1 1

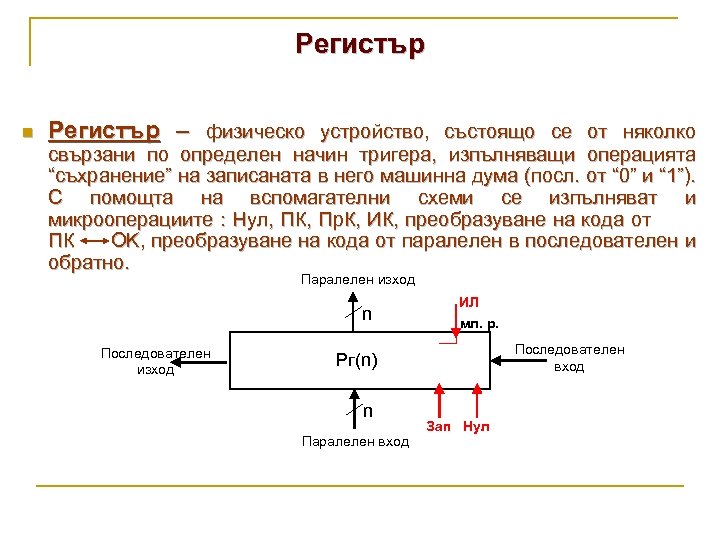Регистър n Регистър – физическо устройство, състоящо се от няколко свързани по определен начин тригера, изпълняващи операцията “съхранение” на записаната в него машинна дума (посл. от “ 0” и “ 1”). С помощта на вспомагателни схеми се изпълняват и микрооперациите : Нул, ПК, Пр. К, ИК, преобразуване на кода от ПК OK, преобразуване на кода от паралелен в последователен и обратно. Паралелен изход n Последователен изход ИЛ мл. р. Последователен вход Рг(n) n Паралелен вход Зап Нул

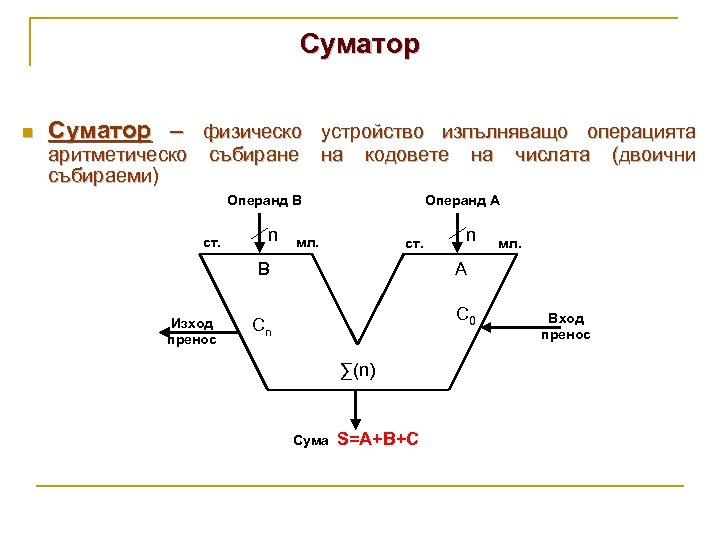Суматор n Суматор – физическо устройство изпълняващо операцията аритметическо събираеми) събиране на кодовете Операнд B ст. n числата Операнд A мл. ст. B Изход пренос на n мл. A C 0 Cn ∑(n) Сума S=A+B+C Вход пренос (двоични

Основни принципи Изчислителният процес в компютъра е напълно автоматизиран благодарение на следните два основни принципа: n Принцип на програмното управление (Чарлз Бейдж 1833 г. ) n Принцип на съхраняваната в паметта на машинната програма за решаване на задачата (Джон фон Нойман 1945 г. )

Основни принципи n Решението на всяка задача се свежда към изпълнението на определена последователност от операции наречена алгоритъм. n За да бъде решена задачата с помощта на компютър, алгоритъмът се записва на езика на машината, при което на всяка операция се поставя в съответствие машинна дума наречена команда, последователността от които образува програмата за решаване на задачата. Програмата се съхранява в ЗУ (ОП).

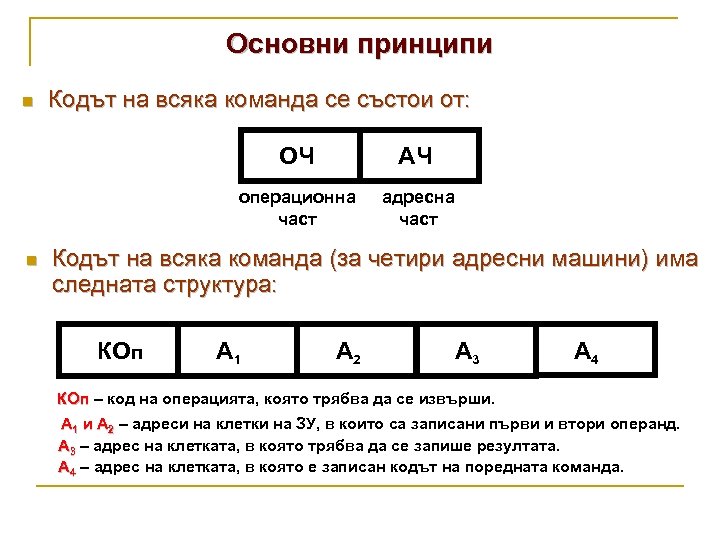Основни принципи n Кодът на всяка команда се състои от: ОЧ операционна част n АЧ адресна част Кодът на всяка команда (за четири адресни машини) има следната структура: КОп А 1 А 2 А 3 А 4 КОп – код на операцията, която трябва да се извърши. А 1 и А 2 – адреси на клетки на ЗУ, в които са записани първи и втори операнд. А 3 – адрес на клетката, в която трябва да се запише резултата. А 4 – адрес на клетката, в която е записан кодът на поредната команда.

Класическа схема на компютърна машина n Централен процесор = АЛУ + УУ АЛУ – аритметико-логическото устройство n УУ – n ЗУ(ОП) – n УВИ – n е предназначено за изпълнение на различни аритметически и логически операции, оперира предимно с кодове на числа (операнди). управляващото устройство синхронизира и управлява работата на отделните устройства в съответствие с изпълняваната програма, оперира с кодове на команди (инструкции). запомнящото устройство е предназначено за приемане, съхранение и предаване на входните данни, междинни и крайни резултати (кодове на числа) и програмата за решаване на задачата. Състои се от множество запомнящи клетки с еднаква разрядност и различни адреси. предназначени са за прочитане на записаната върху носител информация (входни данни + програма), а също и за извеждане на резултата от изпълнението на програмата, т. е решаването на задачата и представянето му в удобен за възприемане вид. Устройства за въвеждане – клавиатура, скенер, мишка и др. Устройства за извеждане – дисплей, принтер, плотер и др. Устройства за въвеждане и извеждане – FDD, HDD, CD-RW, Flash Disk и др.

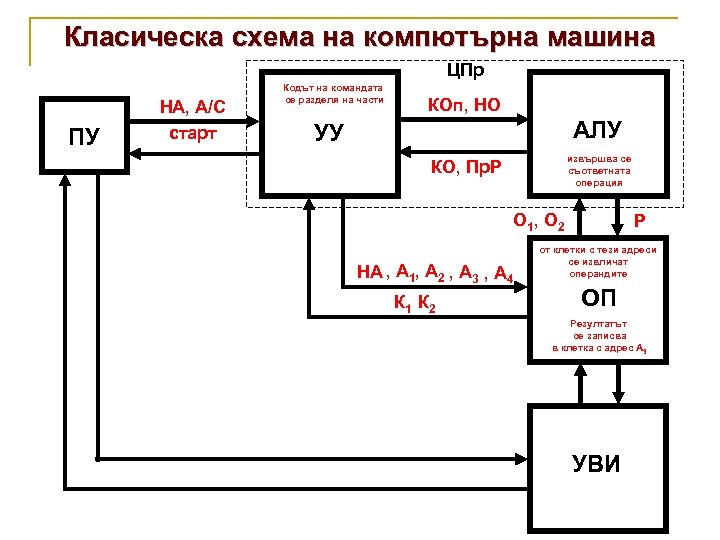Класическа схема на компютърна машина ЦПр ПУ НА, А/С старт Кодът на командата се разделя на части КОп, НО АЛУ УУ извършва се съответната операция КО, Пр. Р О 1 , О 2 НА , А 1, А 2 , А 3 , А 4 К 1 К 2 Р от клетки с тези адреси се извличат операндите ОП от клетка с този адрес Резултатът се извлича записва кодът на с адрес А 3 в клетка командата УВИ

Класическа схема на компютърна машина q q q q Решаването на задачата след въвеждането на входните данни и програмата в ЗУ (ОП) протича в следния порядък: Операторът чрез ПУ записва в съответния регистър на УУ адресът на първата команда на програмата (НА) и подава сигнал за започване на работа, при което става следното: от УУ в ОП – адрес на командата; в ОП от клетката с този адрес се извлича кодът на командата; от ОП в УУ – кодът на командата – К 1; в УУ кодът на командата се разделя на части; от УУ в АЛУ – код на операцията – КОп и НО; от УУ в ОП – А 1 и А 2 (последователно); в ОП от клетки с тези адреси се извличат операндите; от ОП в АЛУ – операнд 1 и операнд 2 (последователно) – О 1 и О 2; в АЛУ се извършва съответната операция; от АЛУ в УУ – КО и Пр. Р (C, OV, N, Z); от УУ в ОП – А 3; от АЛУ в ОП – резултатът Р; в ОП резултатът се записва в клетка с адрес А 3; от УУ в ОП - А 4 и всичко се повтаря отначало.

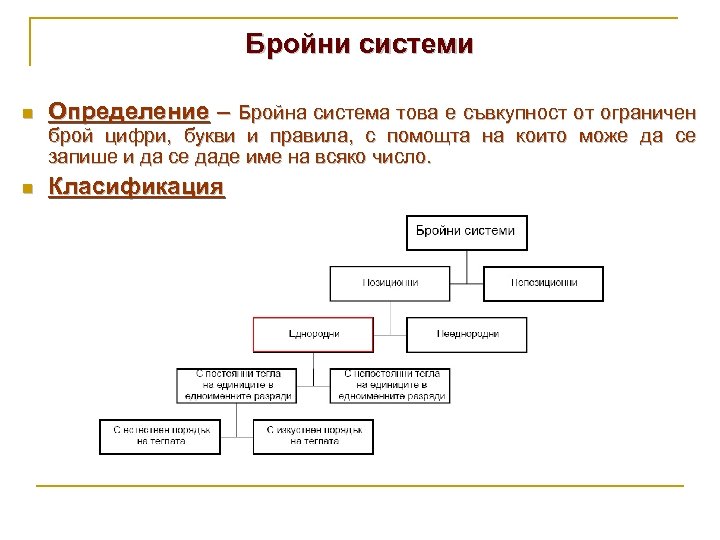Бройни системи n Определение – Бройна система това е съвкупност от ограничен брой цифри, букви и правила, с помощта на които може да се запише и да се даде име на всяко число. n Класификация

Бройни системи n Еднородни системи – Едно число може да бъде записано в еднородна система по следния начин: Ap =anpn-1+an-1 pn-2+…+a 2 p+a 1+a-1 p-1+a-2 p-2+…+a-kp-k където: аi = 0 ÷ (p-1) са разрядни коефициенти; p e основата на системата; pi e теглото на единиците в (i+1)-вия разряд. Пример: Десетична бройна система A 10 =an 10 n-1+an-110 n-2+…+a 210+a 1+a-110 -1+a-210 -2+…+a-k 10 -k 1998 = 1. 103 + 9. 102 + 9. 10 +8

Системи (кодове) с постоянни тегла на разрядите n Адитивен код – Един код е адитивен , ако сумата от кодовете на кои да са две цифри е равна на кода на тяхната сума. n Самодопълващ код – Един код е самодопълващ се , ако за всеки две десетични цифри А и В, сумата на които е 9, е изпълнено условието {A}+{B}=1111.

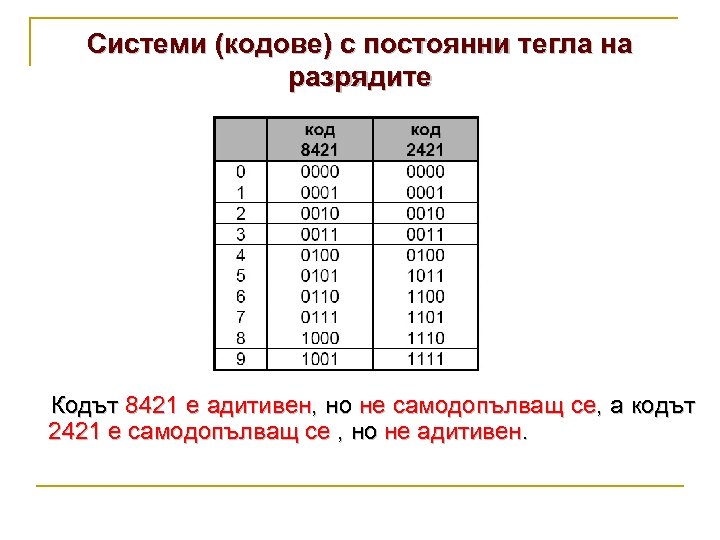Системи (кодове) с постоянни тегла на разрядите Кодът 8421 е адитивен, но не самодопълващ се, а кодът 2421 е самодопълващ се , но не адитивен.

Недостатък на позиционните системи Основен недостатък на позиционните системи е между разрядния пренос, който се получава при извършване на операцията “аритметическо събиране” и води до съществено увеличаване на времето за изпълнение на тази операция. А в компютрите всички аритметични операции с числа се свеждат до поредица от аритметични събирания на техните кодове. Този недостатък липсва при някой непозиционни системи.

Избор на бройна система за използване в компютрите n Основна бройна система – Двоичната. Недостатък – необходимост от преобразуване на входните данни от десетична система в двоична, а на резултатите от двоична в десетична. n Вспомагателни бройни системи – Използват се при обмена на информация между човека и машината – десетична, осмична, шестнадесетична системи.

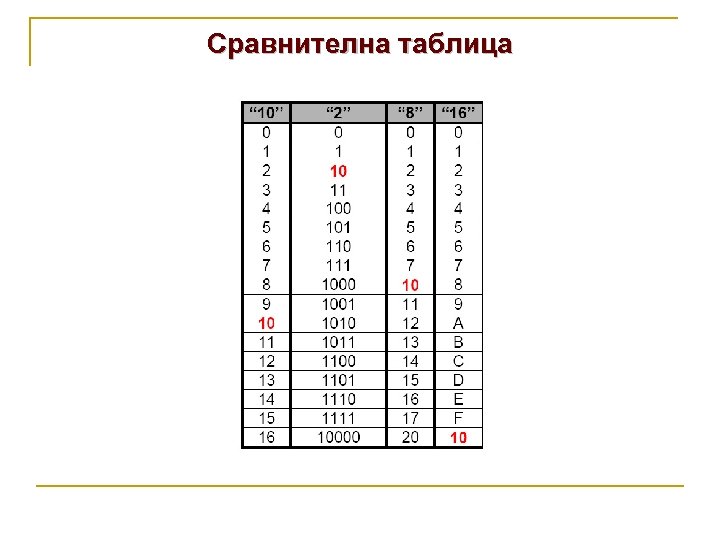Сравнителна таблица

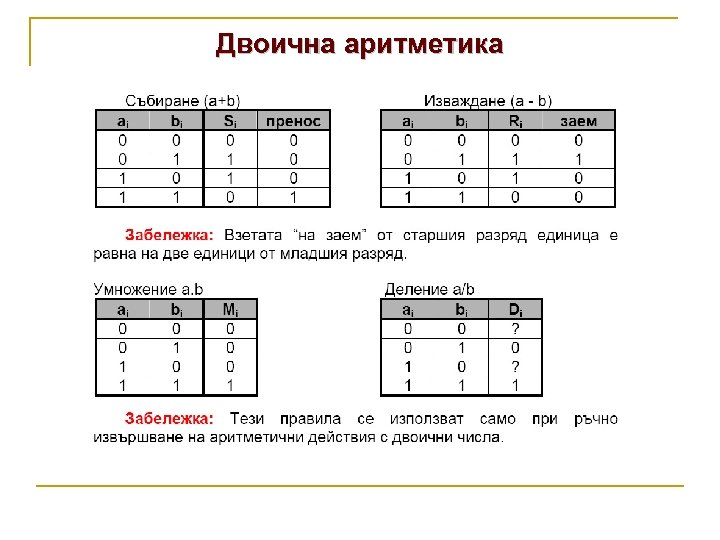Двоична аритметика

Двоична аритметика

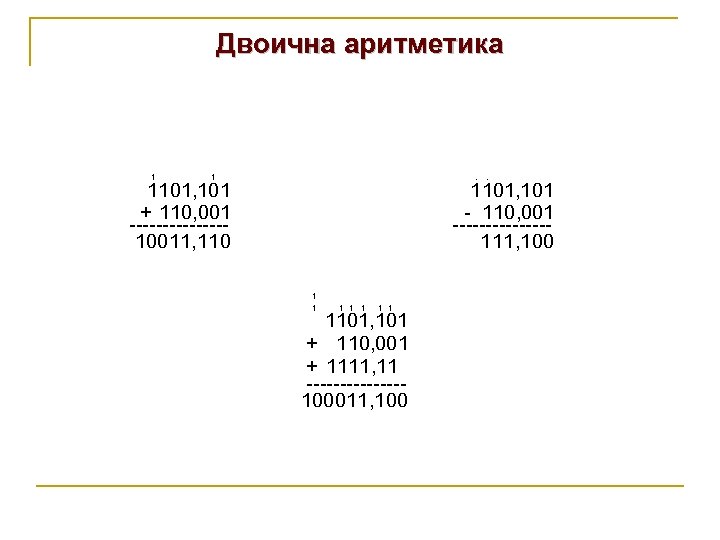Двоична аритметика 1 1 . . 1101, 101 + 110, 001 -------10011, 1101, 101 - 110, 001 -------111, 100 1 1 1 1101, 101 + 110, 001 + 1111, 11 -------100011, 100

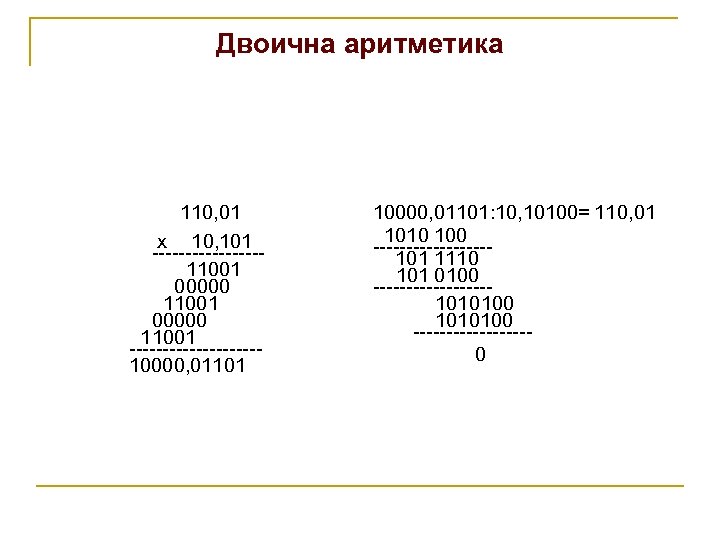Двоична аритметика 110, 01 x 10, 101 --------11001 00000 11001 ----------10000, 01101: 10, 10100= 110, 01 1010 100 ---------101 1110 101 0100 ---------1010100 ---------0