Организация эксперимента Лекция 4 МАТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА

Организация эксперимента Лекция 4

МАТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА Цели планирования • построение многофакторной регрессионной модели; • нахождение значений факторов, при которых отклик оптимален;

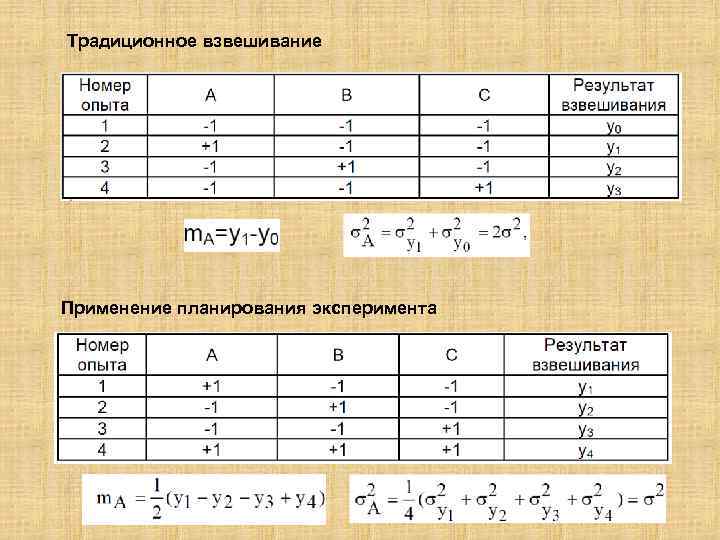Традиционное взвешивание Применение планирования эксперимента

РЕАЛЬНЫЕ И КОДИРОВАННЫЕ ЗНАЧЕНИЯ ФАКТОРОВ - реальные значения факторов; - кодированные значения факторов; - максимальное (верхнее) значение; - минимальное (нижнее) значение; - среднее (основное) значение; - интервал варьирования;

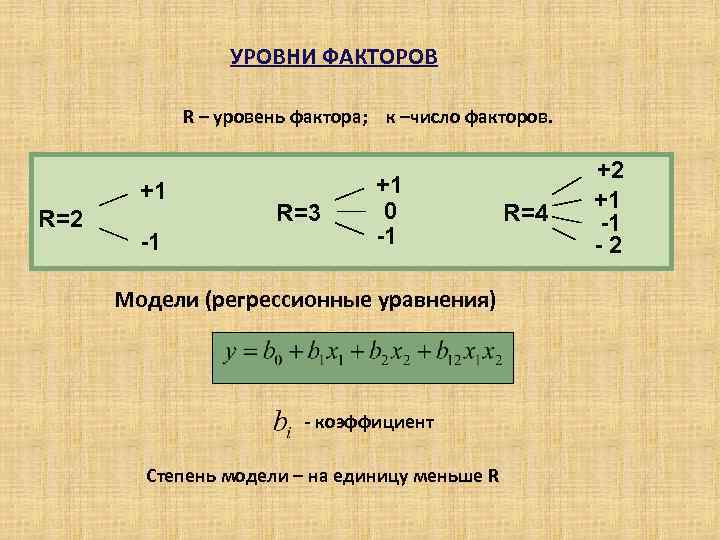УРОВНИ ФАКТОРОВ R – уровень фактора; к –число факторов. +1 R=2 -1 R=3 +1 0 -1 Модели (регрессионные уравнения) - коэффициент Степень модели – на единицу меньше R R=4 +2 +1 -1 -2

ПОЛНЫЙ ФАКТОРНЫЙ ЭКСПЕРИМЕНТ Модель: N = Матрица плана: N = N опыта 1 1 -1 -1 1 2 1 1 -1 -1 3 1 -1 4 1 1 4 0 0 0

СВОЙСТВА ПЛАНА ПФЭ 1. Симметричность 2. Ортогональность 3. Нормированность Регрессионная модель плана главные эффекты взаимодействия

РАСЧЕТ КОЭФФИЦИЕНТОВ УРАВНЕНИЯ ( Это – расчетные значения) - экспериментальные значения (по плану) (принцип МНК)

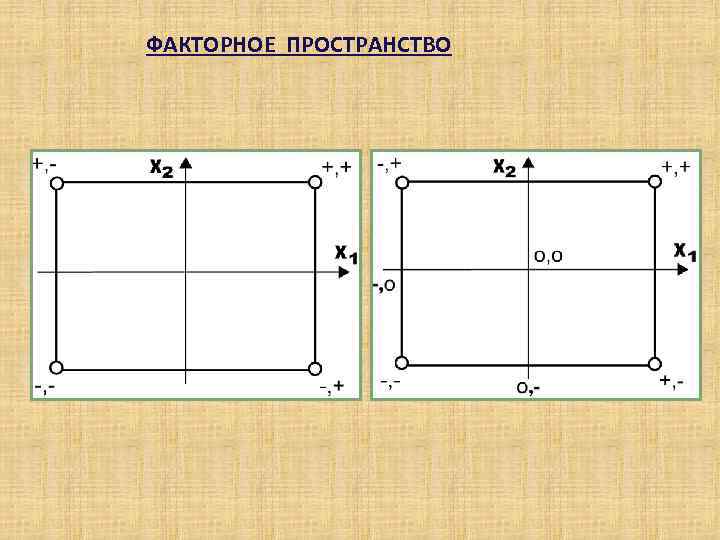ФАКТОРНОЕ ПРОСТРАНСТВО

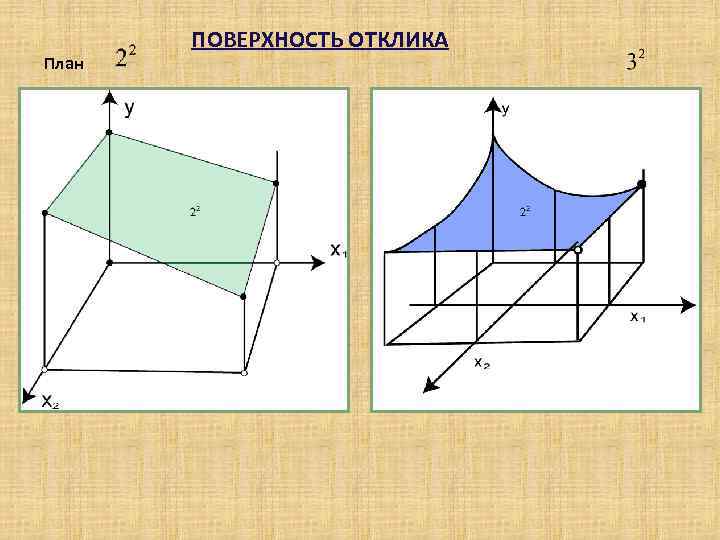План ПОВЕРХНОСТЬ ОТКЛИКА

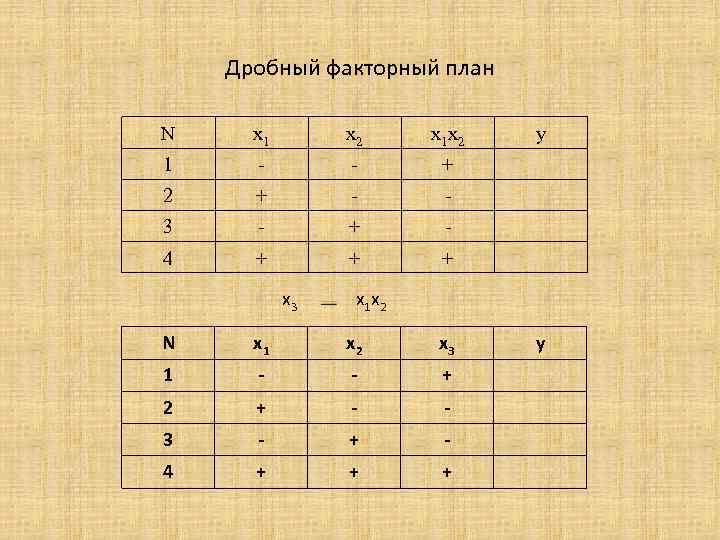Дробный факторный план N x 1 x 2 x 1 x 2 1 - - + 2 + - - 3 - + - 4 + + + x 3 y x 1 x 2 N x 1 x 2 x 3 1 - - + 2 + - - 3 - + - 4 + + + y

Построение математических моделей методом симплексного планирования Симплекс – это выпуклый многогранник с (К+1) вершинами в К-мерном пространстве. Вершины многогранника – опытные точки факторного пространства. В одномерном пространстве - отрезок прямой; В двухмерном – равносторонний треугольник; В трехмерном – правильная треугольная пирамида (тетраэдр).

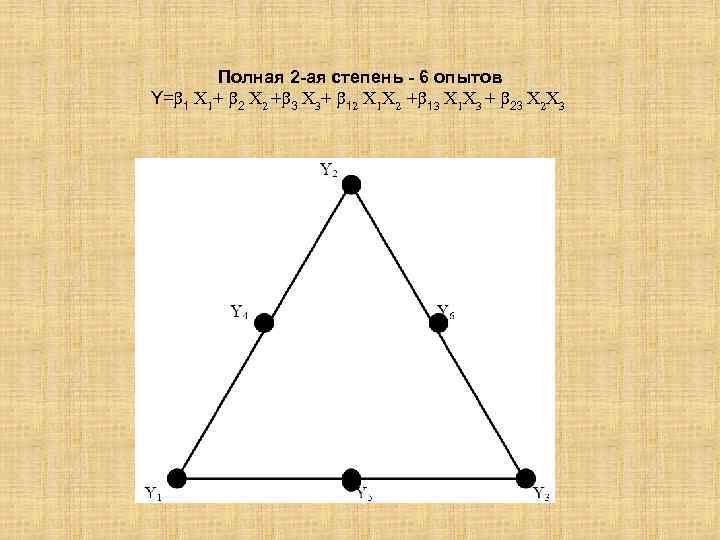Полная 2 -ая степень - 6 опытов Y= 1 X 1+ 2 X 2 + 3 X 3+ 12 X 1 X 2 + 13 X 1 X 3 + 23 X 2 X 3

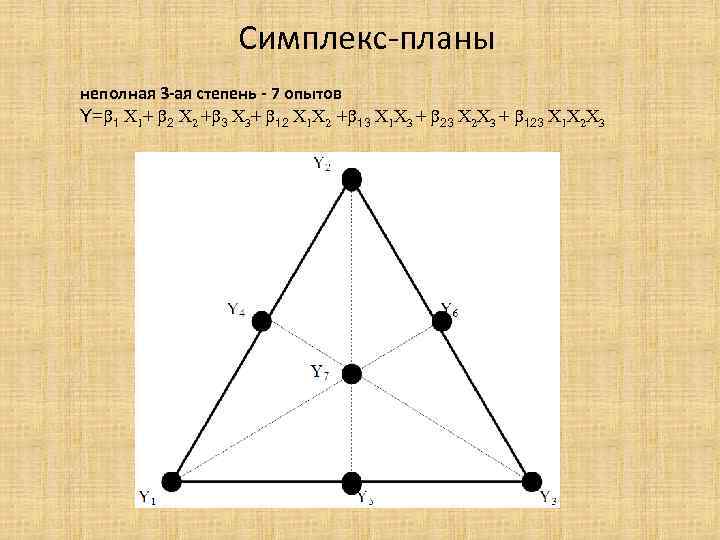Симплекс-планы неполная 3 -ая степень - 7 опытов Y= 1 X 1+ 2 X 2 + 3 X 3+ 12 X 1 X 2 + 13 X 1 X 3 + 23 X 2 X 3 + 123 X 1 X 2 X 3

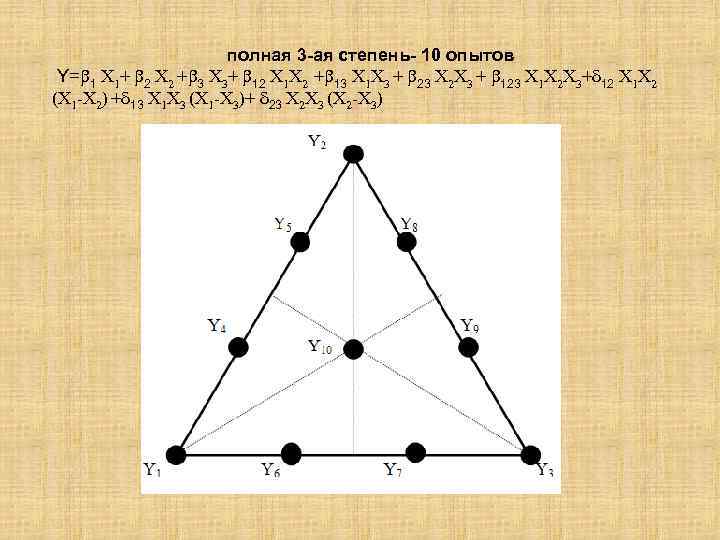полная 3 -ая степень- 10 опытов Y= 1 X 1+ 2 X 2 + 3 X 3+ 12 X 1 X 2 + 13 X 1 X 3 + 23 X 2 X 3 + 123 X 1 X 2 X 3+ 12 X 1 X 2 (X 1 -X 2) + 13 X 1 X 3 (X 1 -X 3)+ 23 X 2 X 3 (X 2 -X 3)

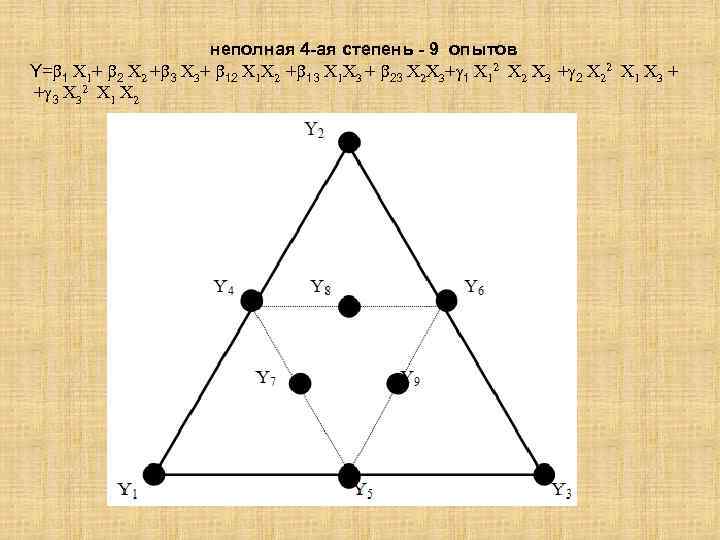неполная 4 -ая степень - 9 опытов Y= 1 X 1+ 2 X 2 + 3 X 3+ 12 X 1 X 2 + 13 X 1 X 3 + 23 X 2 X 3+ 1 X 12 X 3 + 2 X 22 X 1 X 3 + + 3 X 32 X 1 X 2

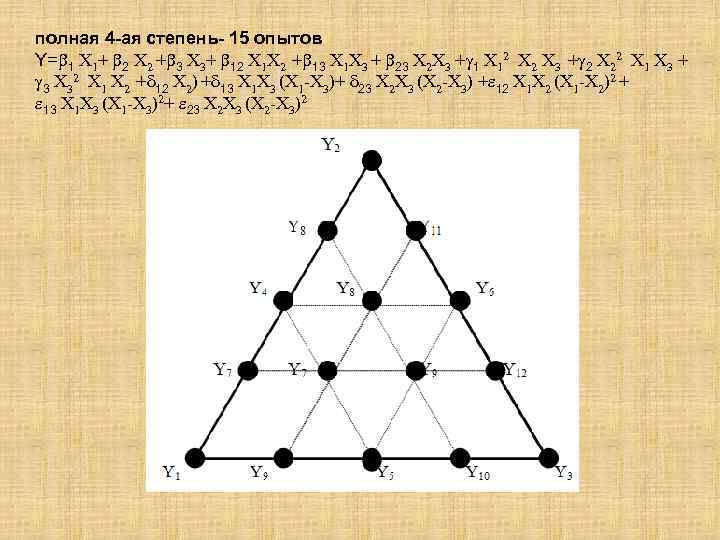полная 4 -ая степень- 15 опытов Y= 1 X 1+ 2 X 2 + 3 X 3+ 12 X 1 X 2 + 13 X 1 X 3 + 23 X 2 X 3 + 1 X 12 X 3 + 2 X 22 X 1 X 3 + 3 X 32 X 1 X 2 + 12 X 2) + 13 X 1 X 3 (X 1 -X 3)+ 23 X 2 X 3 (X 2 -X 3) + 12 X 1 X 2 (X 1 -X 2)2 + 13 X 1 X 3 (X 1 -X 3)2+ 23 X 2 X 3 (X 2 -X 3)2

Проверка значимости (адекватности) уравнения регрессии • - дисперсия адекватности - дисперсия воспроизводимости Условие адекватности Fрас < Fтабл

Поверхность отклика и линии равного уровня

Метод покоординатной оптимизации Достоинство: простота Недостаток: значительное число опытов и большая вероятность неправильного определения экстремума

Метод крутого восхождения

• • • Алгоритм оптимизации методом крутого восхождения. 1. Планирование и постановка ПФЭ (или ДФЭ) в окрестности точки начального состояния xi 0. Расчет коэффициентов bi линейной математической модели с целью определения направления градиента. 2. Расчет произведений biΔxi, где Δxi — интервалы варьирования факторов при ПФЭ (ДФЭ). 3. Выбор базового фактора xi=xi 0, у которого | biΔxi|=a=max. 4. Выбор шага крутого восхождения для базового фактора ha. 5. Расчет шагов изменения других факторов по формуле

• 6. Составление плана движения по градиенту. Для этого в соответствии с определенными значениями шагов изменения факторов и их последовательным алгебраическим суммированием с основным уровнем в точке • • находят координаты опытов 5, 6, 7, 8, 9, 10. 7. В окрестности локального экстремума ставят новую серию опытов (ПФЭ или ДФЭ) для определения новых значений коэффициентов уравнения регрессии и нового направления градиента. В дальнейшем процедура повторяется до достижения следующего локального экстремума и так далее вплоть до определения окрестности координат максимума функции отклика, которая носит название почти стационарной области.

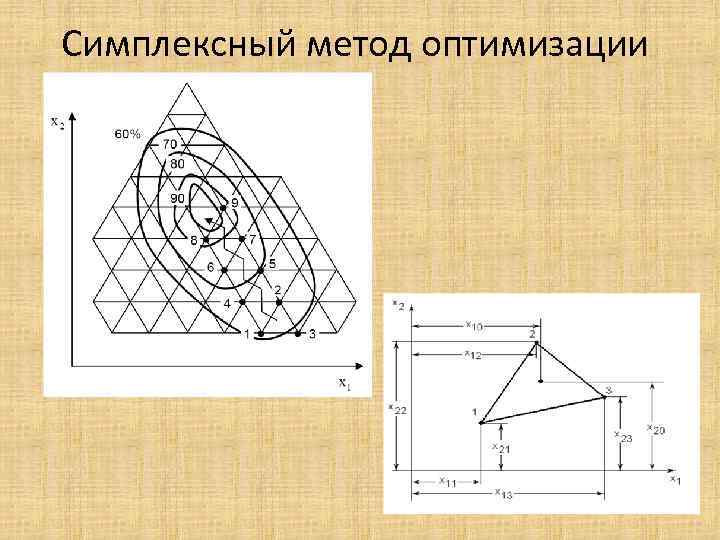Симплексный метод оптимизации

Курсовой проект Провести опрос экспертов для выявления влияния факторов на свойства. Провести статистическую обработку результатов опроса экспертов. Выявить три наиболее влиятельных фактора. В пределах изменения выбранных факторов определить точку ожидаемого экстремума свойства методом крутого восхождения. Вокруг этой точки построить симплекс-модель полной четвертой степени для системы с тремя независимыми факторами (уравнение см. в Приложении А). Точки симплекса на каждой грани тетраэдра расположить как указано в Приложении Б. Один опыт запланировать в центре тетраэдра (x 1= x 2= x 3=0, 25). Проверить модель на адекватность. Построить 3 сечения симплекса при фиксированном значении одного из факторов, равном 0, 2.

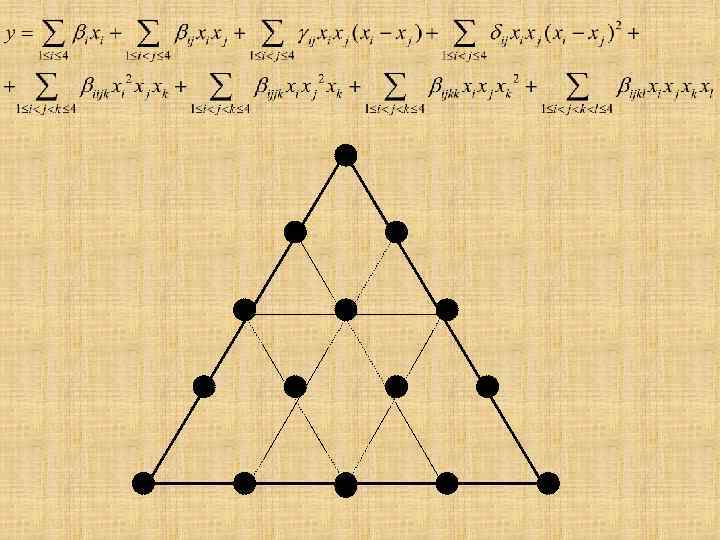
Спасибо за внимание!