Ordered Task Decomposition Theory and Practice Dana S

Ordered Task Decomposition: Theory and Practice Dana S. Nau Dept. of Computer Science, and Institute for Systems Research University of Maryland, College Park, MD Nau: PLANET, 2000 1

Generating Plans of Action l Programs to aid human planners u Project management (consumer software) u Plan storage and retrieval l (e. g. , variant process planning) u Automatic schedule generation (various OR and AI techniques) l For some problems, really want to generate plans automatically u Much more difficult u Very few successful programs for realistic problems l AI planning research is starting to pay off u Of the few really good plan generation systems for practical problems, most involve AI planning techniques u However, … Nau: PLANET, 2000 2

AI Planning Is Different in Practice Than it Was in Theory Unstack(x, y) Pre: on(x, y), clear(x), handempty Del: on(x, y), clear(x), handempty Add: holding(x), clear(y) l Theory: l Practice: u Symbolic computations u Complex numeric computations (STRIPS operators) (geometry, images, probabilities) u Single agent (the planner) u Multiple agents u Perfect information u Imperfect information, external information sources Nau: PLANET, 2000 3

Goal l Develop synergy between theory and applications u By understanding what works Theory Applications in practical planning situations, we can develop better theories of planning u Better theories of planning can lead to better real-world planners Nau: PLANET, 2000 4

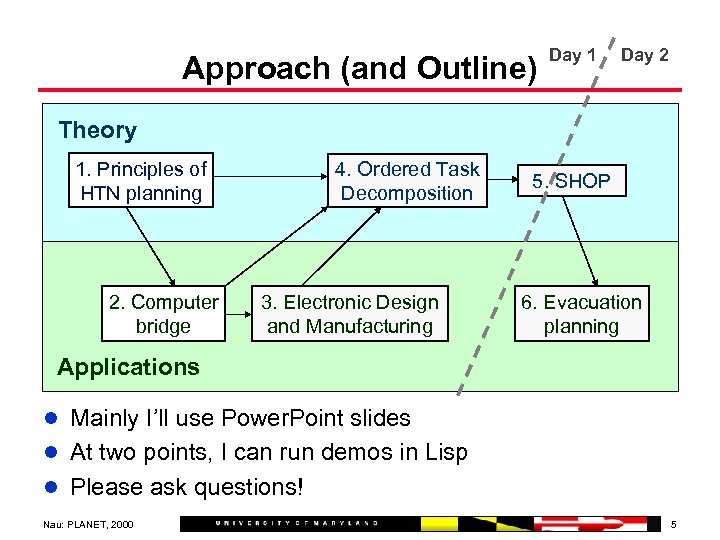Approach (and Outline) Day 1 Day 2 Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Mainly I’ll use Power. Point slides l At two points, I can run demos in Lisp l Please ask questions! Nau: PLANET, 2000 5

1. Principles of HTN Planning Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Joint work with Kutluhan Erol and Jim Hendler Nau: PLANET, 2000 6

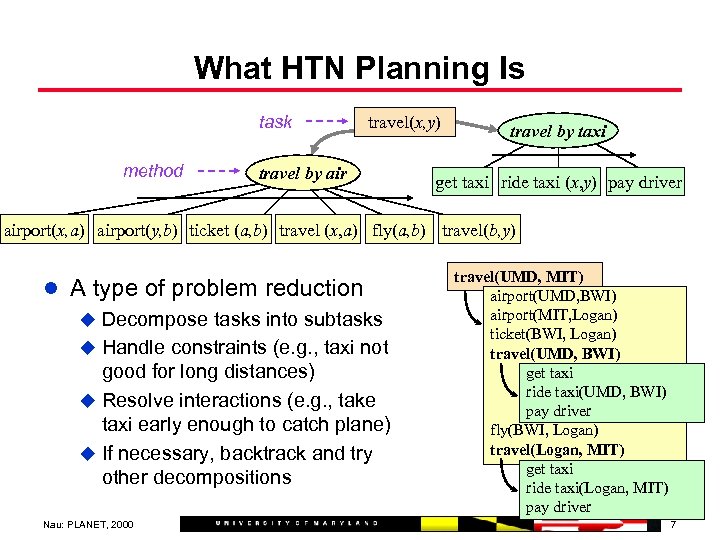What HTN Planning Is task method travel(x, y) travel by air travel by taxi get taxi ride taxi (x, y) pay driver airport(x, a) airport(y, b) ticket (a, b) travel (x, a) fly(a, b) travel(b, y) l A type of problem reduction u Decompose tasks into subtasks u Handle constraints (e. g. , taxi not good for long distances) u Resolve interactions (e. g. , take taxi early enough to catch plane) u If necessary, backtrack and try other decompositions Nau: PLANET, 2000 travel(UMD, MIT) airport(UMD, BWI) airport(MIT, Logan) ticket(BWI, Logan) travel(UMD, BWI) get taxi ride taxi(UMD, BWI) pay driver fly(BWI, Logan) travel(Logan, MIT) get taxi ride taxi(Logan, MIT) pay driver 7

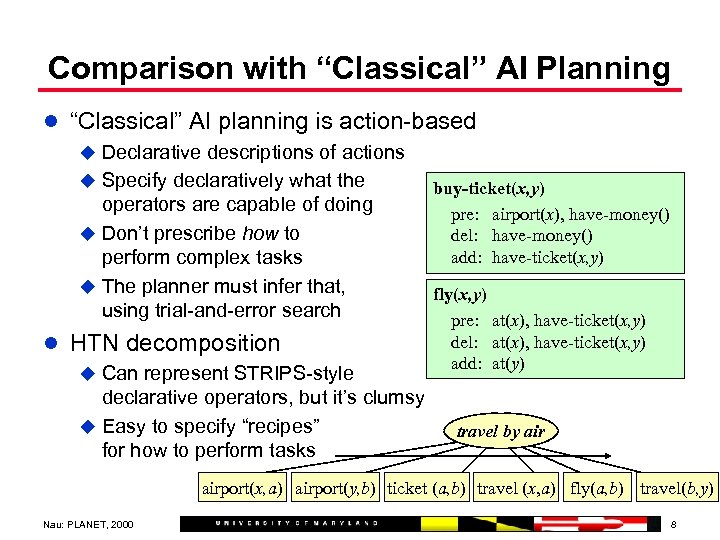Comparison with “Classical” AI Planning l “Classical” AI planning is action-based u Declarative descriptions of actions u Specify declaratively what the buy-ticket(x, y) operators are capable of doing pre: airport(x), have-money() u Don’t prescribe how to del: have-money() add: have-ticket(x, y) perform complex tasks u The planner must infer that, fly(x, y) using trial-and-error search pre: at(x), have-ticket(x, y) l HTN decomposition u Can represent STRIPS-style declarative operators, but it’s clumsy u Easy to specify “recipes” for how to perform tasks del: at(x), have-ticket(x, y) add: at(y) travel by airport(x, a) airport(y, b) ticket (a, b) travel (x, a) fly(a, b) travel(b, y) Nau: PLANET, 2000 8

History of HTN Planning l Originally developed about 25 years ago l [Sacerdoti 1977; Tate 1977] u Long thought to have better potential for applicability to realworld planning problems than classical STRIPS-style planning u Progress delayed due to lack of theoretical understanding l More recent work: theoretical basis for HTN planning u Formal semantics l HTN’s are strictly more expressive than STRIPS operators [Erol et al. , 1994 a] u Sound and complete algorithm [Erol et al. , 1994 b] Implementation available at http: //www. cs. umd. edu/projects/plus/umcp/manual/ u Complexity analysis [Erol et al. , 1996] u This has helped to spread interest in HTN planning Nau: PLANET, 2000 9

What is Expressivity? l Expressivity of languages u A language L is as expressive as another language M iff any expression in L can be translated into an expression with the same meaning in M l Possible ways to define “meaning” 1. based on computational complexity 2. based on model theory 3. based on operational semantics l HTN planning is more expressive than state-based planning according to all three of these definitions u Will summarize all three Nau: PLANET, 2000 1

1. Complexity-Based Expressivity transformation “yes” instances “no” instances Language L Language M l Transformation must preserve answer (“yes” or “no”) l Transformation must be computable/polynomial l Affected by the conciseness of the language Nau: PLANET, 2000 1

HTN Language Versus STRIPS Language l STRIPS-style planning is a special case of HTN planning u Erol [1995] presents two polynomial transformations from the STRIPS planning language to the HTN planning language l There is no computable transformation from the HTN language to the STRIPS language, because HTNs can represent harder problems than the STRIPS language l Example problem: u Given two context-free languages L 1 and L 2, do they have a non-empty intersection? u This problem is undecidable u It can’t be represented as a STRIPS-style planning problem (not unless you augment the STRIPS formalism to include function symbols!) Nau: PLANET, 2000 1

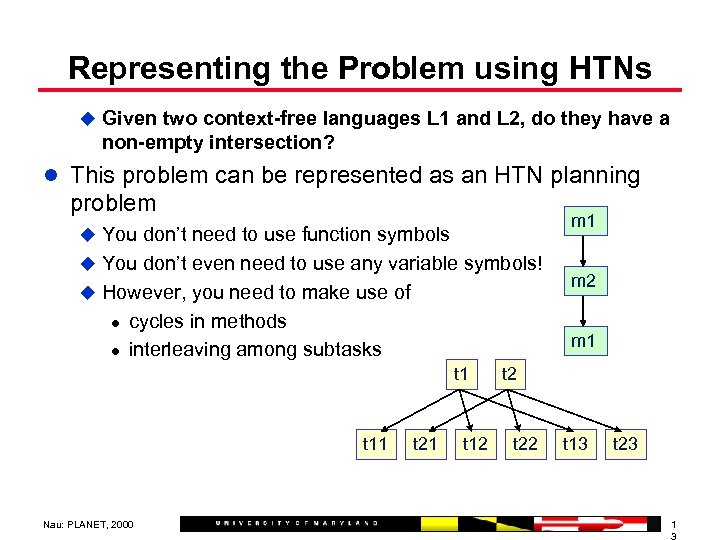Representing the Problem using HTNs u Given two context-free languages L 1 and L 2, do they have a non-empty intersection? l This problem can be represented as an HTN planning problem m 1 u You don’t need to use function symbols u You don’t even need to use any variable symbols! u However, you need to make use of l l cycles in methods interleaving among subtasks m 1 t 11 Nau: PLANET, 2000 m 2 t 21 t 12 t 22 t 13 t 23 1

2. Model-Theoretic Expressivity l Erol [1995] extended the work of Baader on knowledge representation languages to planning languages u The transformation must preserve meaning The set of models satisfying a sentence and the set of models satisfying its tranformation must be equivalent u No restrictions on the computational aspects of the translation l Not affected by the conciseness of the languages l l Result u Erol’s transformations from STRIPS to HTN (mentioned earlier) preserve the set of models u No transformations in the other direction, because HTN models have richer structure u Thus the HTN language is more expressive than the STRIPS language Nau: PLANET, 2000 1

3. Operational-Semantic Expressivity l Transformation must preserve the set of solutions (plans) l Result: u Solutions to STRIPS problems are regular sets u Solutions to HTN problems can be arbitrary context-free sets u Thus HTN’s are more expressive than STRIPS Nau: PLANET, 2000 1

Related Publications [Sacerdoti, 1977] E. Sacerdoti. "A Structure for Plans and Behavior. " American Elsevier Publishing Company, 1977. [Tate, 1977] A. Tate. Generating Project Networks. IJCAI-77, 1977, 888893. [Erol et al. , 1994]K. Erol, J. Hendler and D. S. Nau. Semantics for Hierarchical Task-Network Planning. Tech. Report CS TR-3239, Univ. of Md. , March, 1994. [Erol et al. , 1994 a] K. Erol, J. Hendler and D. S. Nau. HTN Planning: Complexity and Expressivity. In AAAI-94, 1994. [Erol et al. , 1994 b] Erol, Hendler and Nau. UMCP: A Sound and Complete Procedure for Hierarchical Task-Network Planning. In AIPS-94, pp. 249 -254. [Erol, 1995] Erol. Hierarchical Task-Network Planning Systems: Formalization, Analysis, and Implementation. Ph. D. Dissertation, U. of Maryland, 1995. [Erol et al. , 1996]K. Erol, J. Hendler and D. Nau. Complexity Results for Hierarchical Task-Network Planning. Annals of Mathematics and AI, 18: 69 Nau: PLANET, 2000 1 93, 1996.

2. Computer Bridge Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Joint work with Stephen J. Smith and Tom Throop Nau: PLANET, 2000 1

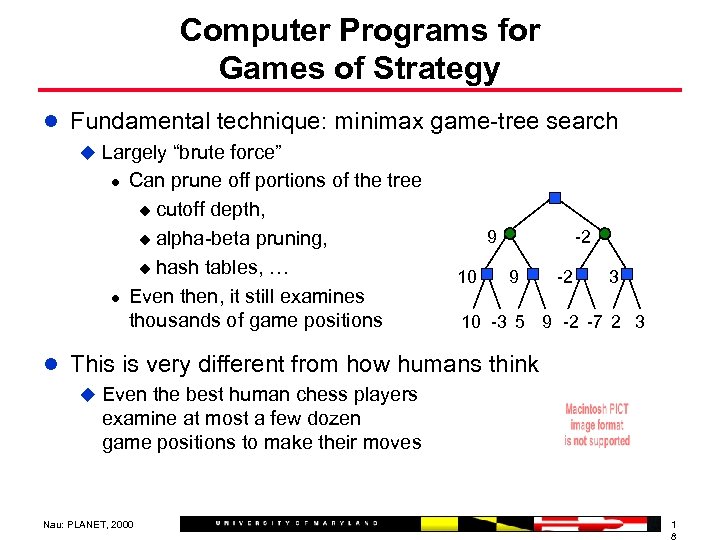Computer Programs for Games of Strategy l Fundamental technique: minimax game-tree search u Largely “brute force” l Can prune off portions of the tree u cutoff depth, 9 -2 u alpha-beta pruning, u hash tables, … 10 9 -2 3 l Even then, it still examines thousands of game positions 10 -3 5 9 -2 -7 2 3 l This is very different from how humans think u Even the best human chess players examine at most a few dozen game positions to make their moves Nau: PLANET, 2000 1

Performance of Game-Playing Computer Programs Connect Four: solved Go-Moku: solved Qubic: solved Nine Men’s Morris: solved Othello: better than humans Checkers: better than any living human Backgammon: better than all but about 10 humans Chess: certainly better than all but about 250 humans; possibly even better than that • • • Bridge: probably worse than the best player at your local bridge club Nau: PLANET, 2000 1

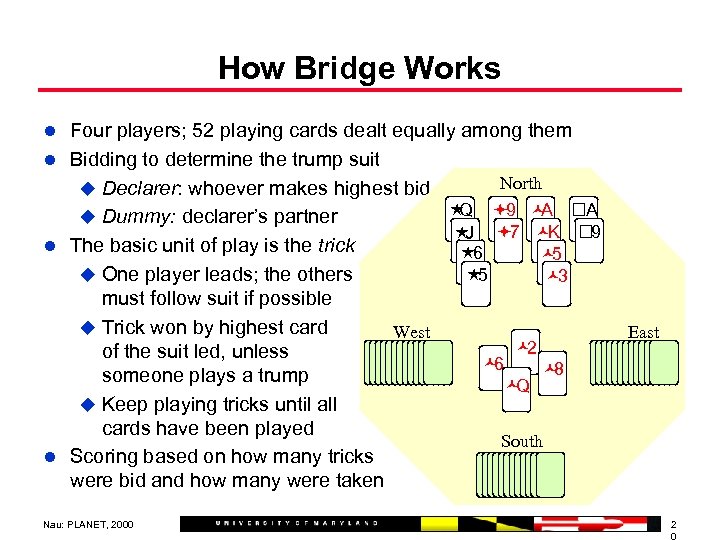How Bridge Works l Four players; 52 playing cards dealt equally among them l Bidding to determine the trump suit u Declarer: whoever makes highest bid u Dummy: declarer’s partner l The basic unit of play is the trick u One player leads; the others must follow suit if possible u Trick won by highest card West of the suit led, unless someone plays a trump u Keep playing tricks until all cards have been played l Scoring based on how many tricks were bid and how many were taken Nau: PLANET, 2000 North 9 A Q A 7 K 9 J 6 5 5 3 6 East 2 Q 8 South 2

Why Bridge is Difficult for Computers l Bridge is an imperfect information game u Don’t know what cards the others have (except the dummy) u Many possible card distributions, so many possible moves l If we encode the additional moves as additional branches in the game tree, this increases the number of nodes exponentially u worst case: about 6 x 1044 leaf nodes u average case: about 1024 leaf nodes Not enough time to search the game tree Nau: PLANET, 2000 2

How to Reduce the Size of the Game Tree? l Bridge is a game of planning u The declarer plans how to play the hand u The plan combines various strategies (ruffing, finessing, etc. ) u If a move doesn’t fit into a sensible strategy, it probably doesn’t need to be considered l Our approach for declarer play u Adaptation of an Hierarchical Task-Network (HTN) planning u Generate a game tree in which each move corresponds to a different strategy, not a different card Brute-force search Our approach Worst case ≈ 6 x 1044 leaf nodes ≈ 305, 000 leaf nodes Average case ≈ 1024 leaf nodes ≈ 26, 000 leaf nodes Nau: PLANET, 2000 2

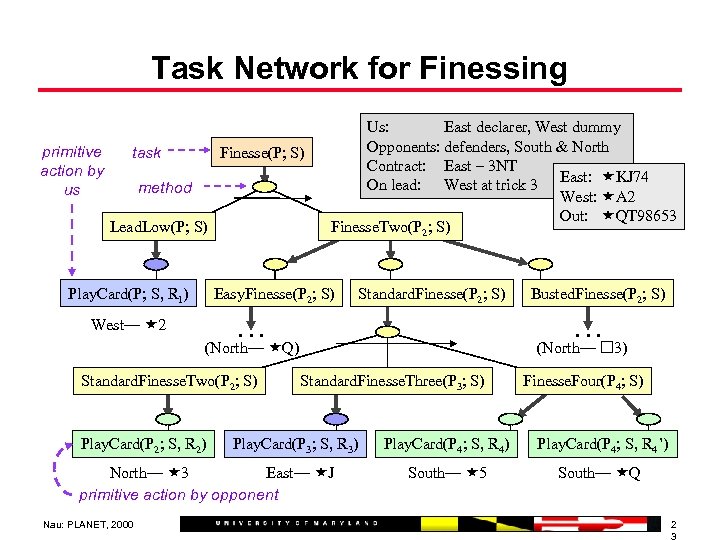Task Network for Finessing primitive action by us task Finesse(P; S) method Lead. Low(P; S) Play. Card(P; S, R 1) Us: East declarer, West dummy Opponents: defenders, South & North Contract: East – 3 NT On lead: West at trick 3 East: KJ 74 West: A 2 Out: QT 98653 Finesse. Two(P 2; S) Easy. Finesse(P 2; S) West— 2 Standard. Finesse(P 2; S) … … (North— Q) Standard. Finesse. Two(P 2; S) Play. Card(P 2; S, R 2) (North— 3) Standard. Finesse. Three(P 3; S) Play. Card(P 3; S, R 3) North— 3 East— J primitive action by opponent Nau: PLANET, 2000 Busted. Finesse(P 2; S) Finesse. Four(P 4; S) Play. Card(P 4; S, R 4’) South— 5 South— Q 2

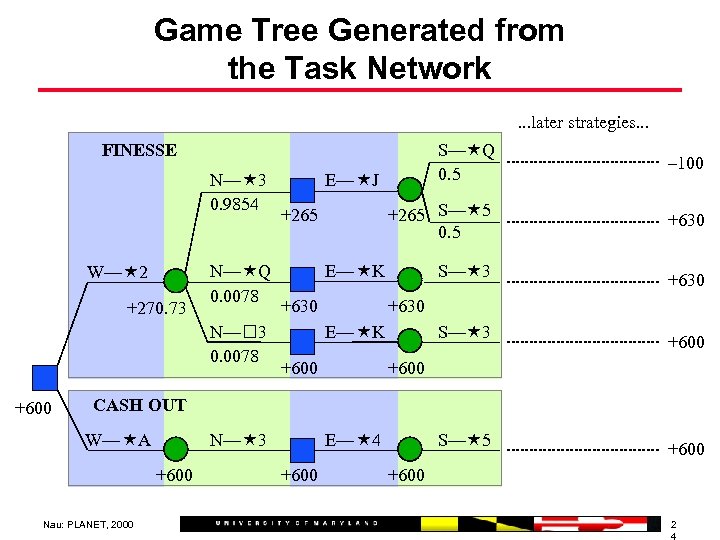Game Tree Generated from the Task Network. . . later strategies. . . FINESSE N— 3 0. 9854 W— 2 +270. 73 N— Q 0. 0078 N— 3 0. 0078 +600 S— Q 0. 5 – 100 +265 S— 5 0. 5 +630 S— 3 +630 E— J +265 E— K +630 E— K +600 S— 3 +600 CASH OUT N— 3 W— A +600 Nau: PLANET, 2000 E— 4 +600 S— 5 +600 2

Implementation l We incorporated our code for declarer play into Bridge Baron (an existing commercial program) l Using our code, Bridge Baron won the 1997 World Bridge Computer Challenge l Our code has been used in all versions of Bridge Baron since October 1997 u Has sold many thousands of copies Nau: PLANET, 2000 2

Related Publications [Smith et al. , 1996] S. J. J. Smith, D. S. Nau, and T. Throop. A Planning Approach to Declarer Play in Contract Bridge. Computational Intelligence, 1996. 12(1): p. 106 -130. [Smith et al. , 1998] S. J. J. Smith, D. S. Nau, and T. Throop. Computer Bridge: A Big Win for AI Planning. AI Magazine, 1998. 19(2): p. 93 -105. Nau: PLANET, 2000 2

3. Electronic Design and Manufacturing Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Joint work with Stephen J. Smith, Kiran Hebbar, and Ioannis Minis Nau: PLANET, 2000 2

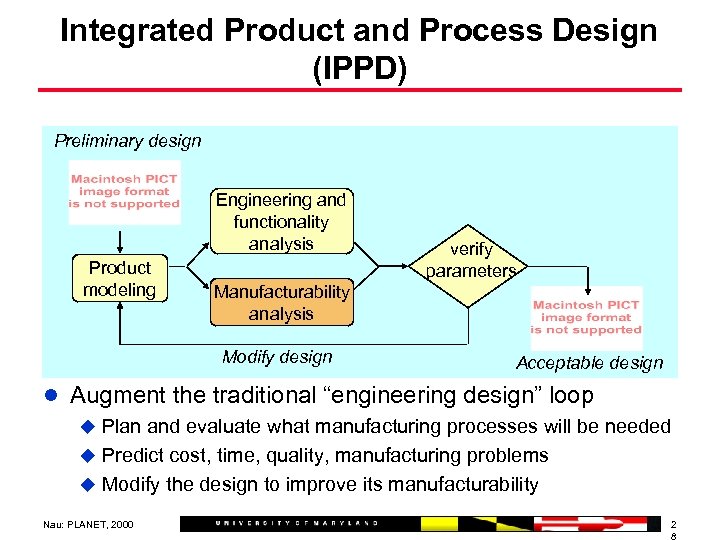Integrated Product and Process Design (IPPD) Preliminary design Engineering and functionality analysis Product modeling verify parameters Manufacturability analysis Modify design Acceptable design l Augment the traditional “engineering design” loop u Plan and evaluate what manufacturing processes will be needed u Predict cost, time, quality, manufacturing problems u Modify the design to improve its manufacturability Nau: PLANET, 2000 2

Microwave Transmit/Receive Modules l 1 -20 GHz frequency range (radars, satellite communications, etc. ) l Difficult and expensive to design and manufacture Nau: PLANET, 2000 2

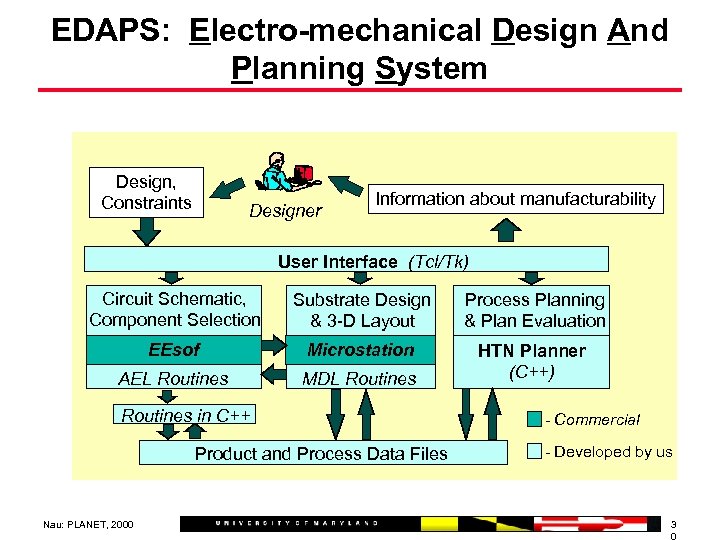EDAPS: Electro-mechanical Design And Planning System Design, Constraints Designer Information about manufacturability User Interface (Tcl/Tk) Circuit Schematic, Component Selection Substrate Design & 3 -D Layout Process Planning & Plan Evaluation EEsof Microstation AEL Routines MDL Routines HTN Planner (C++) Routines in C++ Product and Process Data Files Nau: PLANET, 2000 - Commercial - Developed by us 3

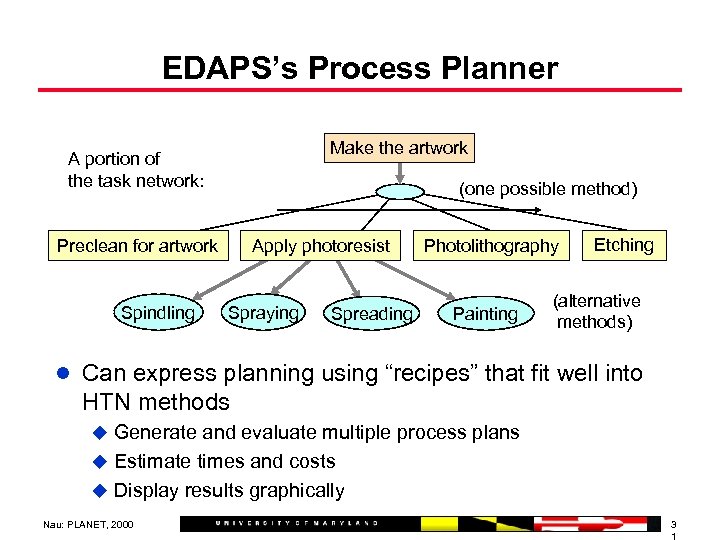EDAPS’s Process Planner Make the artwork A portion of the task network: (one possible method) Preclean for artwork Spindling Apply photoresist Spraying Spreading Photolithography Painting Etching (alternative methods) l Can express planning using “recipes” that fit well into HTN methods u Generate and evaluate multiple process plans u Estimate times and costs u Display results graphically Nau: PLANET, 2000 3

Examples from EDAPS Substrate Dimensions: 7, 4, 1 Ground Material: Aluminum Material: Teflon Substrate thickness: 30 mils Metallized thickness: 7 mils Processes: Opn A BC/WW Setup Runtime LN 001 A VMC 1 2. 00 01 02 03 Description Orient board vertically Clamp board at (1, 1, 1) Establish datum point 001 B VMC 1 0. 10 0. 43 01 Tool: 0. 30 -diameter drill bit 02 Drill at (1. 25, -0. 50 d: 1. 00, f: 50, s: 30 03 Drill at(1. 25, -0. 50) d: 1. 00, f: 20, s: 60 001 C VMC 1 0. 10 0. 77 001 T VMC 1 … 2. 20 1. 20 01 Tool: 0. 20 -diameter slot miller 02 Mi. II start (0. 044, 4. 88) l: 0. 5, w: 0. 5, d: 1. 00, f: 50, s: 40 01 Total time on VMC 1 006 A PLAT 1 1. 00 0. 60 007 A ETR 1 0. 60 0. 50 008 A ETC 1 0. 20 Nau: PLANET, 2000 … 0. 30 02 Dip in bath for 2 minutes Temperature: 100 C, Conc: 1000 ppm 01 Etch plate for 1 minute 01 Etch board for 2 minutes Temperature: 100 C, Conc: 1000 ppm 3

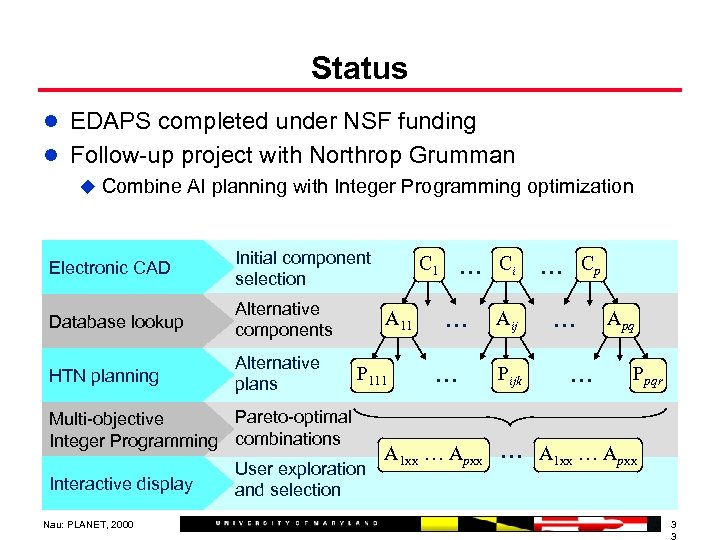Status l EDAPS completed under NSF funding l Follow-up project with Northrop Grumman u Combine AI planning with Integer Programming optimization Electronic CAD Initial component selection Database lookup Alternative components HTN planning Alternative plans A 11 P 111 Pareto-optimal Multi-objective Integer Programming combinations Interactive display Nau: PLANET, 2000 C 1 User exploration and selection … Ci … Cp … … A 1 xx … Apxx Aij Pijk … … Apq Ppqr … A 1 xx … Apxx 3

Related Publications [Hebbar et al. , 1996] K. Hebbar, S. J. Smith, I. Minis and D. Nau. Plan-Based Evaluation of Designs for Microwave Modules. In Proc. ASME Design Technical Conference, August, 1996. [Smith et al. , 1997] S. J. Smith, K. Hebbar, D. Nau, and I. Minis. Integrating Electrical and Mechanical Design and Process Planning. In Knowledge Intensive CAD, Volume 2, M. Mantyla, S. Finger, and T. Tomiyama, Editors. 1997, Chapman and Hall, pp. 269 -288. [Nau et al. , 2000] D. Nau, J. Meyer, M. Ball, J. Baras, A. Chowdhury, E. Lin, R. Rajamani and V. Trichur. Integrated Product and Process Design of Microwave Modules Using AI Planning and Integer Programming. In Fourth Workshop on Knowledge Intensive CAD (KIC-4), 2000, pages 186 -196. Parma, Italy: IFIP Working Group 5. 2. Nau: PLANET, 2000 3

4. Ordered Task Decomposition Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Joint work with Kutluhan Erol, Naresh Gupta, and Stephen J. Smith Nau: PLANET, 2000 3

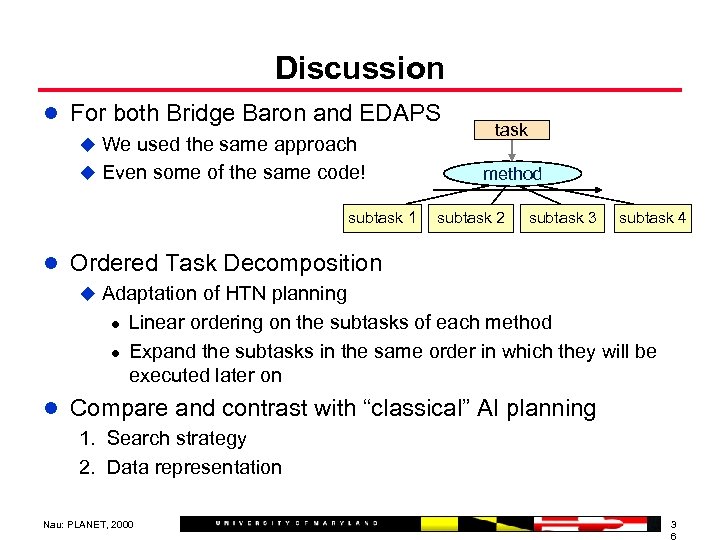Discussion l For both Bridge Baron and EDAPS u We used the same approach u Even some of the same code! subtask 1 task method subtask 2 subtask 3 subtask 4 l Ordered Task Decomposition u Adaptation of HTN planning l Linear ordering on the subtasks of each method l Expand the subtasks in the same order in which they will be executed later on l Compare and contrast with “classical” AI planning 1. Search strategy 2. Data representation Nau: PLANET, 2000 3

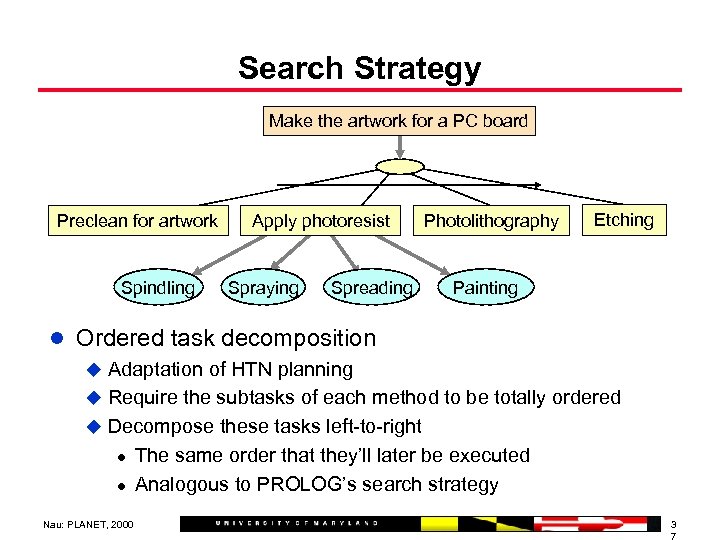Search Strategy Make the artwork for a PC board Preclean for artwork Spindling Apply photoresist Spraying Spreading Photolithography Etching Painting l Ordered task decomposition u Adaptation of HTN planning u Require the subtasks of each method to be totally ordered u Decompose these tasks left-to-right l The same order that they’ll later be executed l Analogous to PROLOG’s search strategy Nau: PLANET, 2000 3

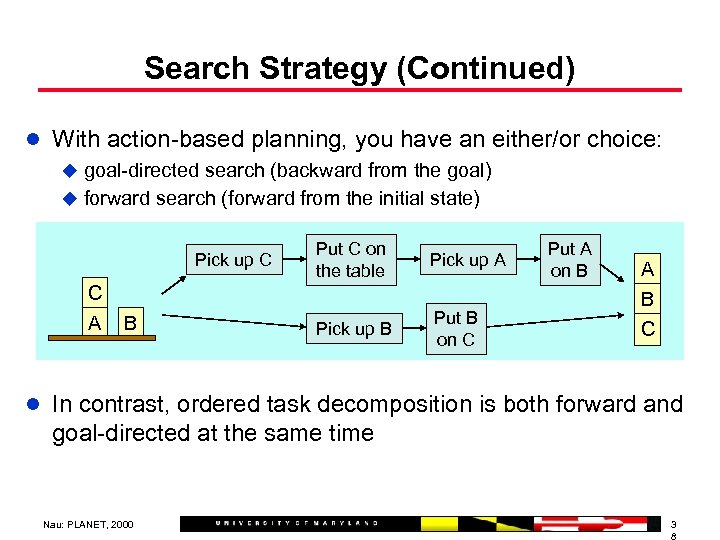Search Strategy (Continued) l With action-based planning, you have an either/or choice: u goal-directed search (backward from the goal) u forward search (forward from the initial state) Pick up C C A B Put C on the table Pick up A Pick up B Put B on C Put A on B A B C l In contrast, ordered task decomposition is both forward and goal-directed at the same time Nau: PLANET, 2000 3

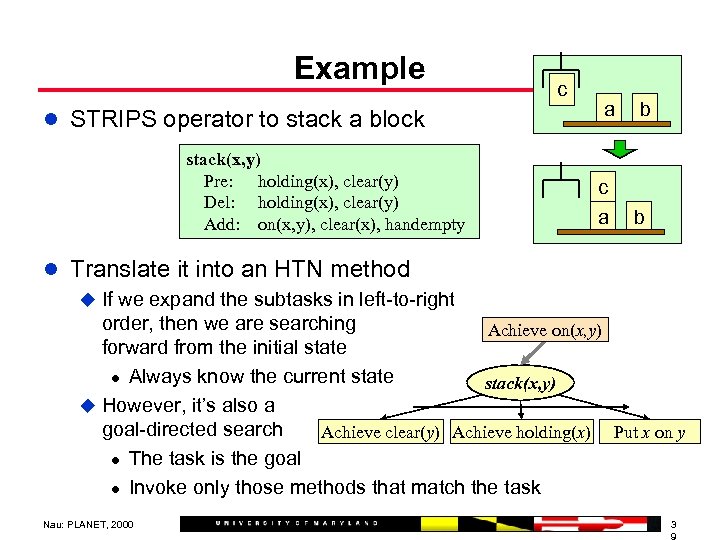Example l STRIPS operator to stack a block stack(x, y) Pre: holding(x), clear(y) Del: holding(x), clear(y) Add: on(x, y), clear(x), handempty c a b l Translate it into an HTN method u If we expand the subtasks in left-to-right order, then we are searching Achieve on(x, y) forward from the initial state l Always know the current state stack(x, y) u However, it’s also a goal-directed search Achieve clear(y) Achieve holding(x) Put x on y l The task is the goal l Invoke only those methods that match the task Nau: PLANET, 2000 3

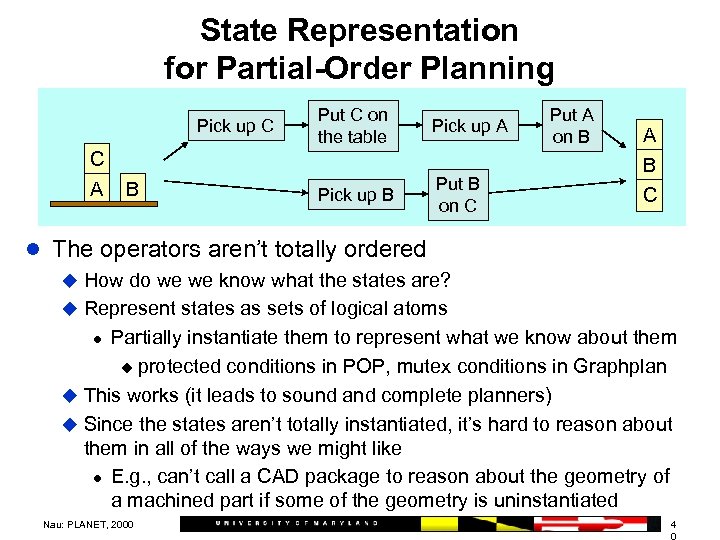State Representation for Partial-Order Planning Pick up C C A B Put C on the table Pick up A Pick up B Put B on C Put A on B A B C l The operators aren’t totally ordered u How do we we know what the states are? u Represent states as sets of logical atoms l Partially instantiate them to represent what we know about them u protected conditions in POP, mutex conditions in Graphplan u This works (it leads to sound and complete planners) u Since the states aren’t totally instantiated, it’s hard to reason about them in all of the ways we might like l E. g. , can’t call a CAD package to reason about the geometry of a machined part if some of the geometry is uninstantiated Nau: PLANET, 2000 4

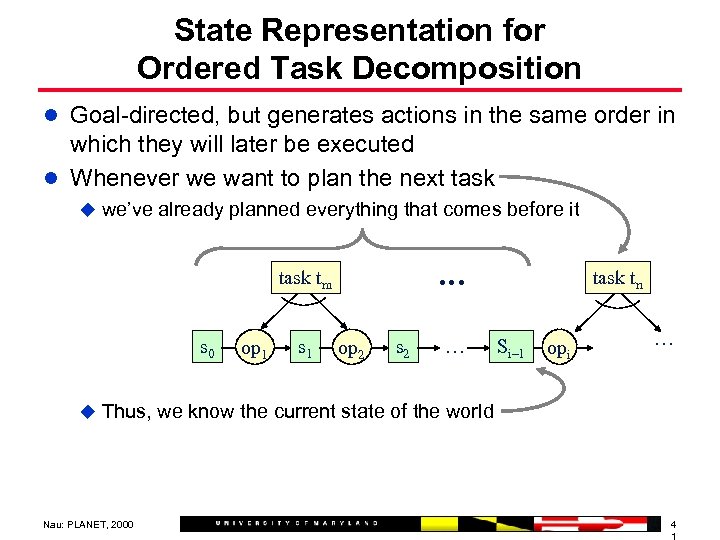State Representation for Ordered Task Decomposition l Goal-directed, but generates actions in the same order in which they will later be executed l Whenever we want to plan the next task u we’ve already planned everything that comes before it … task tm s 0 op 1 s 1 op 2 s 2 … task tn Si– 1 opi … u Thus, we know the current state of the world Nau: PLANET, 2000 4

Increased Expressivity l If we know what the current state is, then we can do complex reasoning about it u Logical inferences u Numeric and probabilistic computations u Interactions with external programs l Example u In computer bridge, by knowing the current state, can decide which of nineteen finesse situations are applicable u With partial-order planning, it would be hard to decide which of them can be made applicable l Can do lots of pruning u Often only one or two consistent “next steps” l Bridge declarer play: complete plans in about 11/2 minutes l Process plans for microwave modules: a few seconds Nau: PLANET, 2000 4

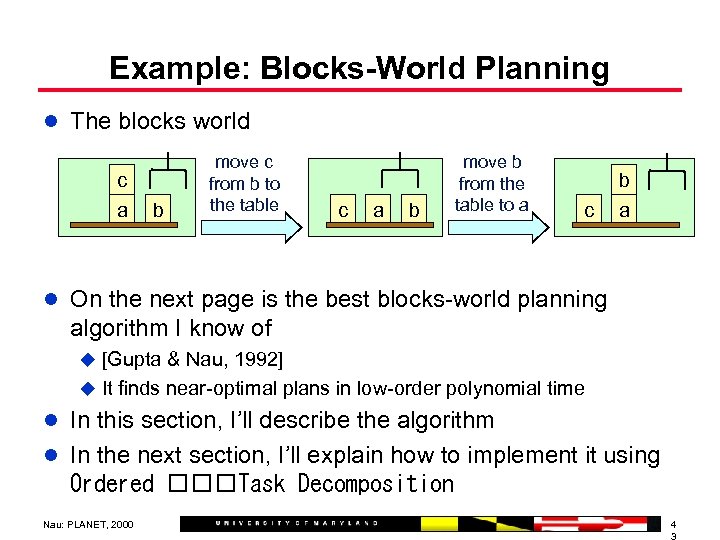Example: Blocks-World Planning l The blocks world c a b move c from b to the table c a b move b from the table to a c b a l On the next page is the best blocks-world planning algorithm I know of u [Gupta & Nau, 1992] u It finds near-optimal plans in low-order polynomial time l In this section, I’ll describe the algorithm l In the next section, I’ll explain how to implement it using Ordered Task Decomposition Nau: PLANET, 2000 4

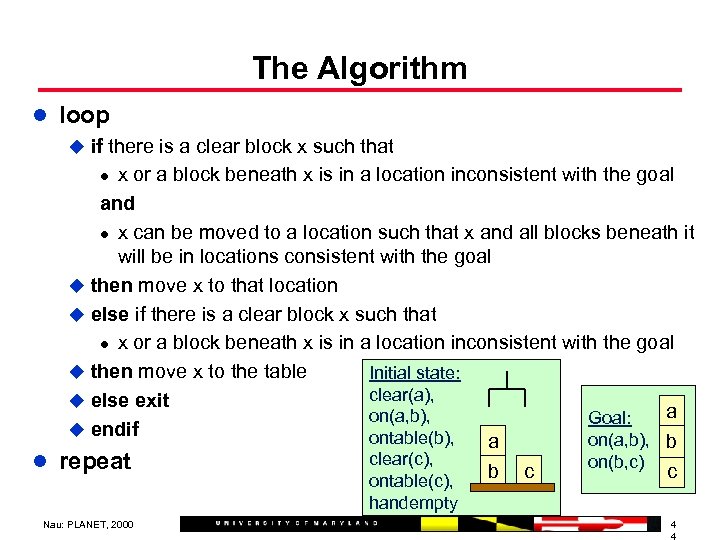The Algorithm l loop u if there is a clear block x such that l x or a block beneath x is in a location inconsistent with the goal and l x can be moved to a location such that x and all blocks beneath it will be in locations consistent with the goal u then move x to that location u else if there is a clear block x such that l x or a block beneath x is in a location inconsistent with the goal u then move x to the table Initial state: clear(a), u else exit a on(a, b), Goal: u endif ontable(b), on(a, b), b a clear(c), on(b, c) l repeat b c c ontable(c), handempty Nau: PLANET, 2000 4

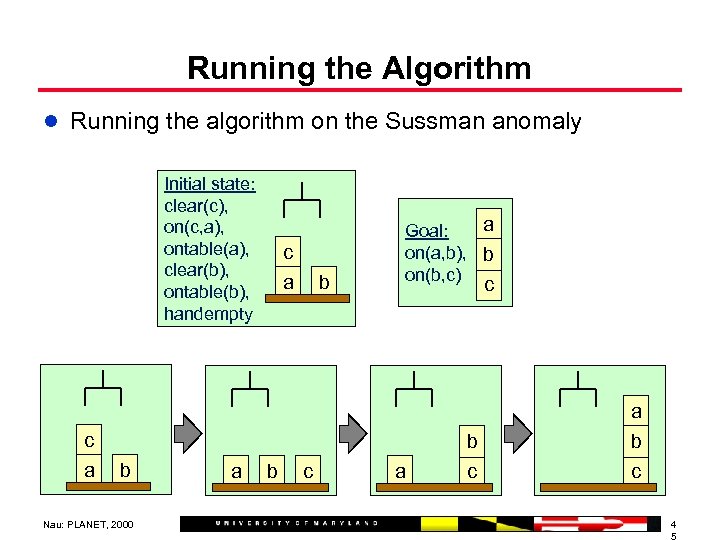Running the Algorithm l Running the algorithm on the Sussman anomaly Initial state: clear(c), on(c, a), ontable(a), clear(b), ontable(b), handempty c a b Nau: PLANET, 2000 a c a b b c a Goal: on(a, b), b on(b, c) c a b c 4

Encoding the Algorithm l loop u if there is a clear block x such that x or a block beneath x is in a location inconsistent with the goal and l x can be moved to a location such that x and all blocks beneath it will be in locations consistent with the goal then move x to that location else if there is a clear block x such that l x or a block beneath x is in a location inconsistent with the goal then move x to the table else exit endif • Can’t write these preconditions using STRIPS-style operators l u u u l repeat Nau: PLANET, 2000 • Can write them as Horn clauses • If we know the current state, we can infer whether they hold • Thus, we can write the algorithm using ordered task decomposition. In the next section, I’ll show to do that 4

Related Publications [Nau et al. , 1998] D. S. Nau, S. J. J. Smith, and K. Erol. Control Strategies in HTN Planning: Theory versus Practice. in AAAI-98/IAAI-98 Proceedings. 1998. [Gupta & Nau, 1992] N. Gupta and D. S. Nau. On the Complexity of Blocks-World Planning. Artificial Intelligence, 56(2 -3): 223 -254, August, 1992. Nau: PLANET, 2000 4

5. SHOP Theory 1. Principles of HTN planning 2. Computer bridge 4. Ordered Task Decomposition 3. Electronic Design and Manufacturing 5. SHOP 6. Evacuation planning Applications l Joint work with Yue Cao, Amnon Lotem, and Héctor Muñoz-Avila Nau: PLANET, 2000 4

SHOP (Simple Hierarchical Ordered Planner) l Domain-independent algorithm for Ordered Task Decomposition u Sound/complete across a large number of planning domains l Implementation u Common-Lisp implementation available at http: //www. cs. umd. edu/projects/shop u Developing a Java implementation Nau: PLANET, 2000 4

Input and Output l Input: u State: a set of ground atoms u Task List: a linear list of tasks u Domain: methods, operators, axioms l Output: one or more plans u depending on what we tell SHOP to look for, it can return l the first plan it finds l all possible plans l a least-cost plan l all least-cost plans l etc. Nau: PLANET, 2000 5

Elements of the Input l State: collection of ground atoms (in Lisp notation) u ((at home) (have-cash 50. 43) (distance home downtown 10)) l Task list: linear list of tasks to perform u ((travel home downtown) (buy book)) l Each method: task, preconditions and decomposition l Preconditions to be established using logical inference l Decomposition is a task list l Each axiom: Horn clause u Extensions: may contain negations and calls to the Lisp evaluator l Each primitive operator: task, delete list, add list u Like a STRIPS operator, but without the preconditions u Performs a primitive task Nau: PLANET, 2000 5

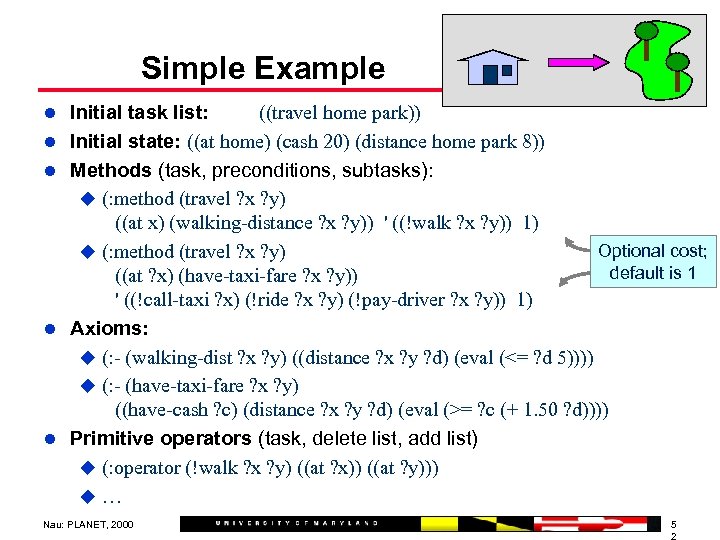Simple Example l Initial task list: l l ((travel home park)) Initial state: ((at home) (cash 20) (distance home park 8)) Methods (task, preconditions, subtasks): u (: method (travel ? x ? y) ((at x) (walking-distance ? x ? y)) ' ((!walk ? x ? y)) 1) Optional cost; u (: method (travel ? x ? y) default is 1 ((at ? x) (have-taxi-fare ? x ? y)) ' ((!call-taxi ? x) (!ride ? x ? y) (!pay-driver ? x ? y)) 1) Axioms: u (: - (walking-dist ? x ? y) ((distance ? x ? y ? d) (eval (<= ? d 5)))) u (: - (have-taxi-fare ? x ? y) ((have-cash ? c) (distance ? x ? y ? d) (eval (>= ? c (+ 1. 50 ? d)))) Primitive operators (task, delete list, add list) u (: operator (!walk ? x ? y) ((at ? x)) ((at ? y))) u… Nau: PLANET, 2000 5

The SHOP Algorithm state S; task list T=( t , …) 1 2 procedure SHOP (state S, task-list T, domain D) operator instance o 1. if T = nil then return nil 2. t 1 = the first task in T state o(S) ; task list T=(t 2, …) 3. U = the remaining tasks in T 4. if t is primitive & an operator instance o matches t 1 then 5. P = SHOP (o(S), U, D) nondeterministic choice 6. if P = FAIL then return FAIL among all methods m 7. return cons(o, P) whose preconditions can 8. else if t is non-primitive be inferred from S & a method instance m matches t 1 in S & m’s preconditions can be inferred from S then 9. return SHOP (S, append (m(t 1), U), D) 10. else task list T=( t 1 , t 2, …) 11. return FAIL method instance m 12. end if end SHOP task list T=( u 1, …, uk , t 2, …) Nau: PLANET, 2000 5

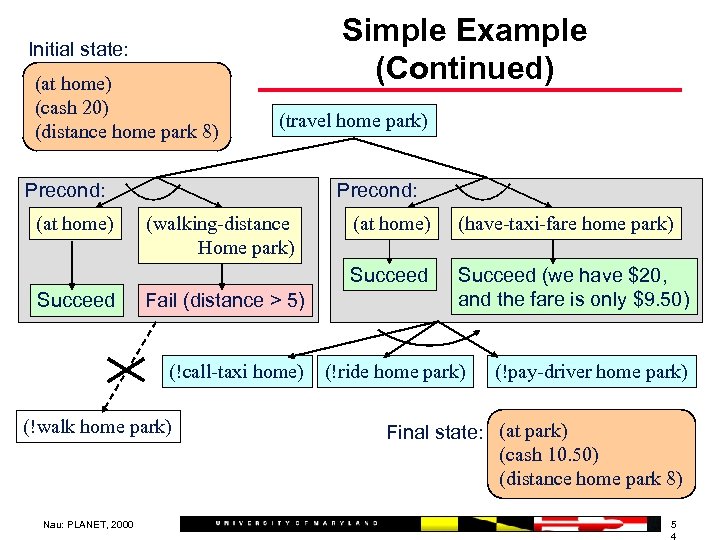Simple Example (Continued) Initial state: (at home) (cash 20) (distance home park 8) (travel home park) Precond: (at home) Precond: Fail (distance > 5) (!call-taxi home) (!walk home park) Nau: PLANET, 2000 (at home) (have-taxi-fare home park) Succeed (walking-distance Home park) Succeed (we have $20, and the fare is only $9. 50) (!ride home park) (!pay-driver home park) Final state: (at park) (cash 10. 50) (distance home park 8) 5

Question l I can run SHOP for you right now, on a slightly more complicated version of the example. l Would you like me to do so? Nau: PLANET, 2000 5

Homework Assignment l Formulate a plan for going to the beach l Execute the plan Nau: PLANET, 2000 5