Option Contracts 5 -1 DEFINITIONS The

Option Contracts 5 -1

DEFINITIONS • The option holder has the right to buy the underlying instrument at the call’s exercise (strike) price • 5 -2 Call: Put: The option holder has the right to sell the underlying instrument at the put’s exercise (strike) price

WRITTEN OPTIONS UNDER FAS 133 A written option is sold by an "option writer" who sells options collateralized by a portfolio of securities or other performance bonds. Typically a written option is more than a mere "right" in that it requires contractual performance based upon another party's right to force performance. The issue with most written options is not whether they are covered by FAS 133 rules. The issue is whether they will be allowed to be designated as cash flow hedges. Written options are referred to at various points in FAS 133. For example, see Paragraphs 20 c, 28 c, 91 -92 (Example 6), 199, and 396 -401. . For rules regarding written options see Paragraphs 396 -401 on Pages 179 -181 of FAS 133. Exposure Draft 162 -B would not allow hedge accounting for written options. FAS 133 relaxed the rules for written options under certain circumstances explained in Paragraphs 396 -401. Note that written options may only hedge recorded assets and liabilities. They may not be used to hedge forecasted purchase and sales transactions. 5 -3

PURCHASED OPTIONS UNDER FAS 133 Purchased options are widely used for hedging and present some of the biggest challenges for hedge accounting rules. The major problem is that purchased option values are often highly volatile relative to value changes in the hedged item. Traditional Delta effectiveness tests fail for hedge accounting for full value. 5 -4

OPTION PARTICIPANTS Call Buyer Pays premium Has the right to buy Put Buyer Pays premium Has the right to sell 5 -5 Call Seller Collects premium Has obligation to sell, if assigned Put Seller Collects premium Has obligation to buy, if assigned

IDENTIFYING OPTIONS • Call or put • Strike price (exercise price) • Expiration date • Underlying instrument 5 -6

Option Strategies http: //www. optionetics. com/education/strategies. asp Bullish Strategies • Calls: • Covered Calls: • Vertical Spread: • Bull Call Spread • Bull Put Spread Bearish Strategies : • Buying Puts • Covered Puts: Bear • Call Spread • Bear Put Spread 5 -7

Delta Hedging http: //biz. yahoo. com/glossary/bfglosd. html Delta hedge where delta = d(Option)/d(spot) = Hedge Ratio A dynamic hedging strategy using options with continuous adjustment of the number of options used, as a function of the delta of the option. Delta neutral The value of the portfolio is not affected by changes in the value of the asset on which the options are written. 5 -8

Dynamic Hedging http: //biz. yahoo. com/glossary/bfglosd. html Dynamic hedging A strategy that involves rebalancing hedge positions as market conditions change; a strategy that seeks to insure the value of a portfolio using a synthetic put option. 5 -9

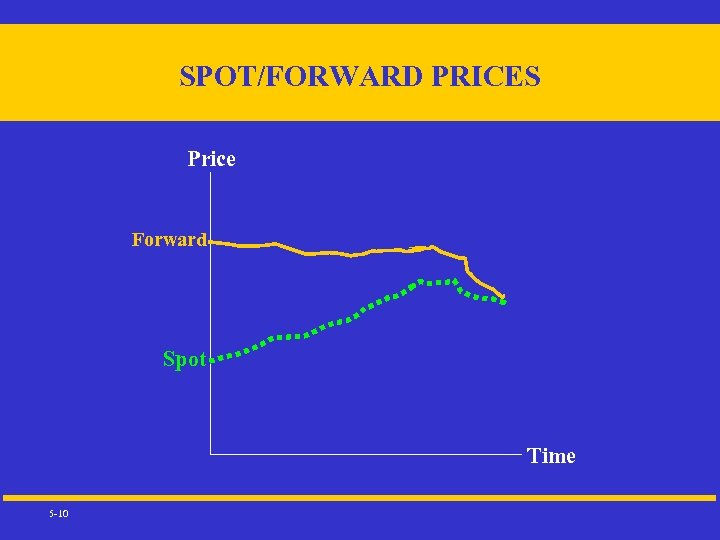SPOT/FORWARD PRICES Price Forward Spot Time 5 -10

TIME VALUE / VOLATILITY VALUE • Time value is the option premium less intrinsic value – Intrinsic value is the beneficial difference between the strike price and the price of the underlying • Volatility value is the option premium less the minimum value – Minimum value is present value of the beneficial difference between the strike price and the price of the underlying 5 -11

FEATURES OF OPTIONS Option Value = Intrinsic Value + Time Value • Intrinsic Value: • Time Value: 5 -12 Difference between the strike price and the underlying price, if beneficial; otherwise zero Sensitive to time and volatility; equals zero at expiration

Sub-paragraph b(c) of Paragraph 63 of FAS 133 c. If the effectiveness of a hedge with a forward or futures contract is assessed based on changes in fair value attributable to changes in spot prices, the change in the fair value of the contract related to the changes in the difference between the spot price and the forward or futures price would be excluded from the assessment of hedge effectiveness. 5 -13

Sub-paragraph b(a) of Paragraph 63 of FAS 133 a. If the effectiveness of a hedge with an option contract is assessed based on changes in the option's intrinsic value, the change in the time value of the contract would be excluded from the assessment of hedge effectiveness. 5 -14

Sub-paragraph b(b) of Paragraph 63 of FAS 133 b. If the effectiveness of a hedge with an option contract is assessed based on changes in the option's minimum value, that is, its intrinsic value plus the effect of discounting, the change in the volatility value of the contract would be excluded from the assessment of hedge effectiveness. 5 -15

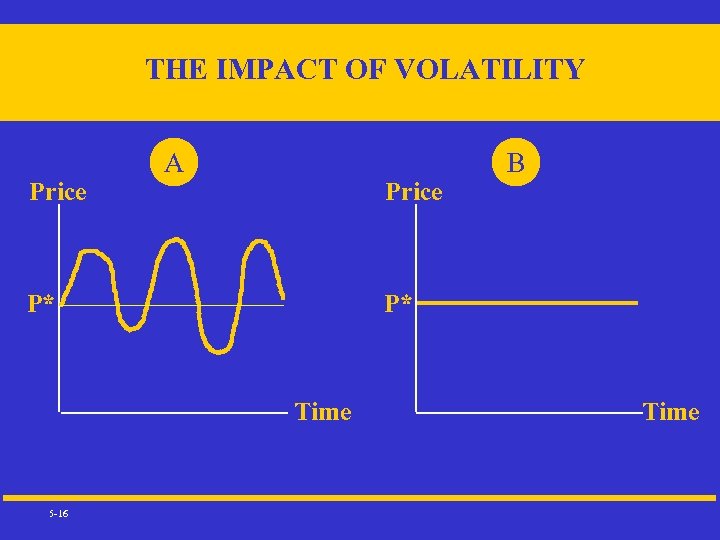THE IMPACT OF VOLATILITY Price A Price P* P* Time 5 -16 B Time

Minimum Value Option Value = Risk Free Value + Volatility Value If the underlying is the price of corn, then the minimum value of an option on corn is either zero or the current spot price of corn minus the discounted risk-free present value of the strike price. In other words if the option cannot be exercised early, discount the present value of the strike price from the date of expiration and compare it with the current spot price. If the difference is positive, this is the minimum value. It can hypothetically be the minimum value of an American option, but in an efficient market the current price of an American option will not sell below its risk free present value. 5 -17

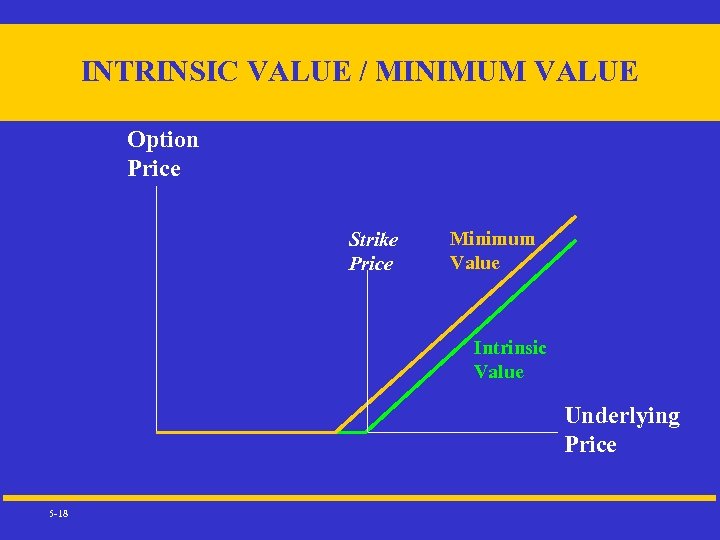INTRINSIC VALUE / MINIMUM VALUE Option Price Strike Price Minimum Value Intrinsic Value Underlying Price 5 -18

Minimum (Risk Free) Versus Intrinsic Value European Call Option • • X = Exercise (Strike) Price in n periods after current time P = Current Price (Underlying) of Commodity • I = P-X>0 is the intrinsic value using the current spot price if the option is in the money • M = is the minimum value at the current time • M>I if the intrinsic value I is greater than zero Value of Option exceeds minimum M due to volatility value 5 -19

Minimum (Risk Free) Versus Intrinsic Value Arbitrate for European Call Option • • X = $20 Exercise (Strike) Price and Minimum Value M = $10. 741 n = 1 year with risk-free rate r = 0. 08 P (Low) = $10 with PV(Low) = $9. 259 P = $20 such that the intrinsic value now is I = P-X = $10. Borrow P(Low), and Buy at $20 = $9. 259+10. 741 = PV(Low)+M If the ultimate price is low at $10 after one year, pay off loan at P(Low)=$10 by selling the commodity at $10. If we also sold an option for M=$10. 741, ultimately our profit would be zero from the stock purchase and option sale. If the actual option value is anything other than M=$10. 741, it would be possible to arbitrage a risk free gain or loss. 5 -20

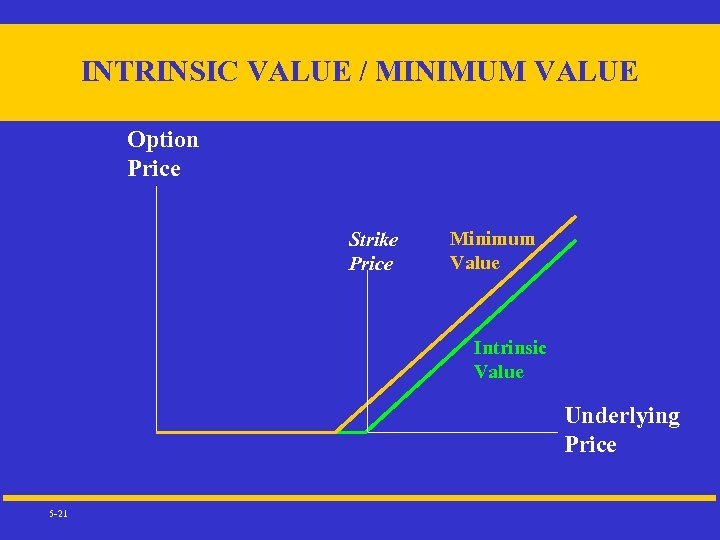INTRINSIC VALUE / MINIMUM VALUE Option Price Strike Price Minimum Value Intrinsic Value Underlying Price 5 -21

Minimum Versus Intrinsic Value American Call Option • • X = Exercise (Strike) Price in n periods after current time P = Current Price (Underlying) of Commodity • I = P-X>0 is the intrinsic value using the current spot price if the option is in the money • M = 0 is the minimum value since option can be exercised at any time if the option’s value is less than intrinsic value I. Value of option exceeds M and I due to volatility value 5 -22

What’s Wrong With the Black-Scholes Model When Valuing Options? • The Black-Scholes Model works pretty well for options on stocks. It does not work well for interest rate and some commodity options. • The main problem for interest rates is the assumption that shortterm interest rates are constant. • The assumption of constant variance is always a worry when using this model to value any type of option. • The assumption of normality is always a worry when using this model for valuing options of any type. 5 -23

LONG OPTION HEDGES • Fair value hedges – Mark-to-market of the option will generally be smaller than exposure’s contribution to earnings • Cash flow hedges – Changes in intrinsic values of options go to – other comprehensive income to the extent effective* Remaining changes in option prices goes to current income * Bounded by the magnitude of the exposures’ price changes 5 -24

GENERAL RECOMMENDATIONS • • For most fair value hedges: Exclude forward points from hedge effectiveness considerations • For non-interest rate cash flow hedges: Assess effectiveness based on comparisons of forward prices • 5 -25 For most static option hedges: Exclude time value from hedge effectiveness considerations For options: Consider the FAS Paragraph 167 alternative for minimum value hedging.

“THE RISK BEING HEDGED” • For non-interest rate exposures – Entities must identify their firm-specific exposures as hedged items – Differences between firm-specific prices and hedging instruments’ underlying variables will foster income volatility – Pre-qualifying hedge effectiveness documentation is required for all crosshedges 5 -26

Selected IAS 39 Paragraph Excerpts • • 146. 80%

FAS Effectiveness Testing --- http: //www. qrm. com/products/mb/Rmbupdate. htm • • • Dollar Offset (DO) calculates the ratio of dollar change in profit/loss for hedge and hedged item Relative Dollar Offset (RDO) calculates the ratio of dollar change in net position to the initial MTM value of hedged item Variability Reduction Measure (Var. RM) calculates the ratio of the squared dollar changes in net position to the squared dollar changes in hedged item Ordinary Least Square (OLS) measures the linear relationship between the dollar changes in hedged item and hedge. OLS calculates the coefficient of determination (R 2) and the slope coefficient (ß) for effectiveness measure and accounts for the historical performance Least Absolute Deviation (LAD) is similar to OLS, but employs median regression analysis to calculate R 2 and ß. 5 -28

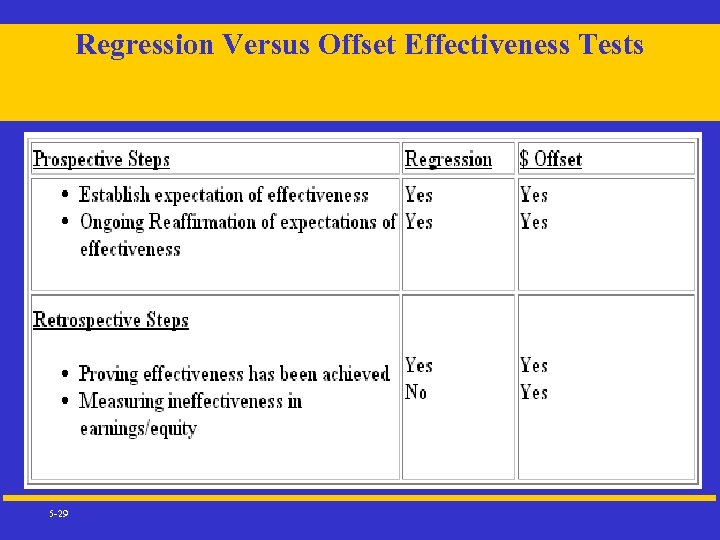Regression Versus Offset Effectiveness Tests 5 -29

The Dictionary of Financial Risk Management defines dynamic hedging as follows --- http: //snipurl. com/Dynamic. Hedging • 5 -30 Dynamic Hedging: A technique of portfolio insurance or position risk management in which an option-like return pattern is created by increasing or reducing the position in the underlying (or forwards, futures or short -term options in the underlying) to simulate the Delta change in value of an option position. For example, a short stock futures index position may be increased or decreased to create a synthetic put on a portfolio, producing a portfolio insurance-type return pattern. Dynamic hedging relies on liquid and reasonably continuous markets with low to moderate transaction costs. See Continuous Markets, Delta Hedge, Delta/Gamma Hedge, Portfolio Insurance.

Dynamic Hedging Paragraph 144 of IAS 39 Reads as Follows 144. There is normally a single fair value measure for a hedging instrument in its entirety, and the factors that cause changes in fair value are co-dependent. Thus a hedging relationship is designated by an enterprise for a hedging instrument in its entirety. The only exceptions permitted are (a) splitting the intrinsic value and the time value of an option and designating only the change in the intrinsic value of an option as the hedging instrument, while the remaining component of the option (its time value) is excluded and (b) splitting the interest element and the spot price on a forward. Those exceptions recognize that the intrinsic value of the option and the premium on the forward generally can be measured separately. A dynamic hedging strategy that assesses both the intrinsic and the time value of an option can qualify for hedge accounting. 5 -31

New Example Coming Up 5 -32

Example 9, Para 162, FAS 133 Appendix B Cash Flow Hedge Using Intrinsic Value • XYZ specified that hedge effectiveness will be measured based on changes in intrinsic value • The American call option purchased at 1/1/X 1 has a four-month term • The call premium is $9. 25, the strike rate is $125, and the option is currently at-the-money See 133 ex 09 a. xls at http: //www. cs. trinity. edu/~rjensen/ • • 5 -33 Also see http: //www. trinity. edu/rjensen/caseans/Intrinsic. Value. htm

Example 9 from FAS 133 Paragraph 162 With 100% Delta Effectiveness Forecasted Transaction Option Entry Time Intrinsic Date Value Jan. 01 $125. 00 $9. 25 = Premium $0 $0. 00 = Intrinsic Value $9. 25 = Time Value 5 -34

Example 9 from FAS 133 Paragraph 162 January 31 Forecasted Transaction Option Entry Time Intrinsic Date Value Jan. 01 $125. 00 $9. 25 $0 Debit Credit Balance Jan. 01 Call option 9. 25 Cash 9. 25 (9. 25) For cash flow hedges, adjust hedging derivative to fair value and offset to OCI to the extent of hedge effectiveness. 5 -35

Example 9 from FAS 133 Paragraph 162 With 100% Delta Effectiveness Forecasted Transaction Option Total Entry Time Intrinsic Option Date Value Jan. 01 $125. 00 $9. 25 = Premium $0 $9. 25 Jan. 31 $127. 25 $7. 50 $2. 25 $9. 75 $2. 25 = Change in Hedged Intrinsic Value $2. 25 = Change in Hedge Contract Intrinsic Value Delta = 1. 00 or 100% based on intrinsic value Delta = 0. 44 = 44% = |(9. 75 -9. 25)/ (127. 25 -125. 00)| 5 -36

Example 9 from FAS 133 Paragraph 162 January 31 Forecasted Transaction Option Entry Time Intrinsic Date Value Jan. 01 $125. 00 $9. 25 $0 Jan. 31 $127. 25 $7. 50 $2. 25 Debit Credit Balance Jan. 31 Call option 0. 50 9. 75 P&L 1. 75 OCI 2. 25 (2. 25) For cash flow hedges, adjust hedging derivative to fair value and offset to OCI to the extent of hedge effectiveness. 5 -37

Example 9 from FAS 133 Paragraph 162 February 28 Forecasted Transaction Option Entry Time Intrinsic Date Value Jan. 31 $127. 25 $7. 50 $2. 25 Feb. 28 $125. 50 $5. 50 $0. 50 Debit Credit Balance Feb. 28 OCI 1. 75 (0. 50) P&L 2. 00 3. 75 Call option 3. 75 6. 00 For cash flow hedges, adjust hedging derivative to fair value and offset to OCI to the extent of hedge effectiveness. 5 -38

Example 9 from FAS 133 Paragraph 162 March 31 Forecasted Transaction Option Total Entry Time Intrinsic Option Date Value Feb. 28 $125. 50 $5. 50 $0. 50 $6. 00 Mar. 31 $124. 25 $3. 00 $0. 00 $3. 00 Debit Credit Balance Mar. 31 OCI 0. 50 0 P&L 2. 50 6. 25 Call option 3. 00 For cash flow hedges, adjust hedging derivative to fair value and offset to OCI to the extent of hedge effectiveness. 5 -39

Example 9 from FAS 133 Paragraph 162 April 30 Forecasted Transaction Option Total Entry Time Intrinsic Option Date Value Jan. 01 $125. 00 $9. 25 $0. 00 $9. 25 Mar. 31 $124. 25 $3. 00 $0. 00 $3. 00 Apr. 30 $130. 75 $0. 00 $5. 75 Debit Credit Balance Apr. 30 Call option 2. 75 5. 75 P&L 3. 00 9. 25 OCI 5. 75 5 -40

Example 9 from FAS 133 Paragraph 162 With No Basis Adjustment Under FAS 133 Debit Credit Balance Apr. 30 Cash 5. 75 -$3. 50 Call option 5. 75 $0 Apr. 30 OCI No basis adjustment yet P&L No basis adjustment yet Apr. 30 Inventory 130. 75 $130. 75 Cash 130. 75 -$134. 25 Cash = -$9. 25 Premium +$5. 75 Call Option - $130. 75 = -$134. 25 5 -41

Example 9 from FAS 133 Paragraph 162 With No Basis Adjustment Under FAS 133 Debit Credit Balance May 14 Cash 234. 25 +$100. 00 P&L (or Sales) 234. 25 -$225. 00 May 14 P&L (or CGS) 130. 75 -$ 94. 25 Inventory 130. 75 $ 0 May 14 OCI 5. 75 $ 0 P&L 5. 75 -$100. 00 5 -42

Example 9 from FAS 133 Paragraph 162 With Basis Adjustment Under IAS 39 Debit Credit Apr. 30 Cash 5. 75 Call option 5. 75 Apr. 30 OCI 5. 75 P&L 5. 75 Apr. 30 Inventory 130. 75 Cash 130. 75 5 -43

FUTURES /FORWARDS vs. OPTIONS Futures / Forwards Long Options Unlimited risk/reward Limited risk/unlimited reward No initial payment Initial payment of premium Offsets risk and opportunity Offsets risk/allows opportunity 5 -44

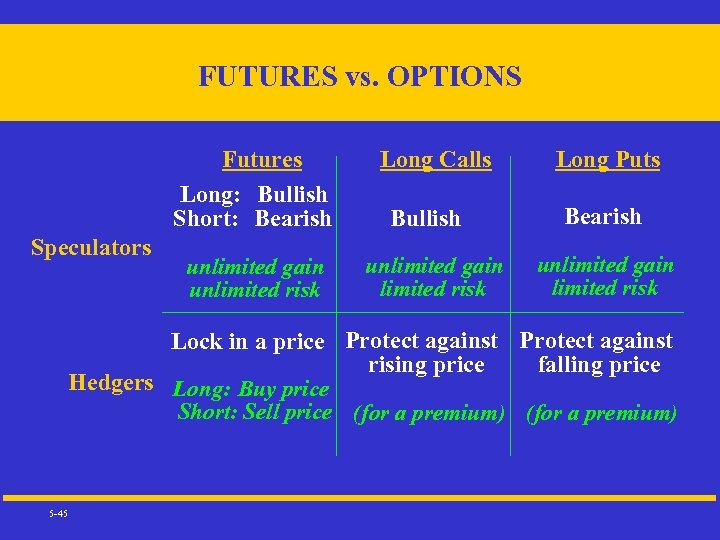FUTURES vs. OPTIONS Futures Long: Bullish Short: Bearish Speculators Long Calls unlimited gain unlimited risk unlimited gain limited risk Bullish Long Puts Bearish unlimited gain limited risk Lock in a price Protect against rising price falling price Hedgers Long: Buy price Short: Sell price (for a premium) 5 -45

OPTION VALUATION PRACTICES • • Where no market is available – Requires “marking-to-model” – Valuations will differ depending on the particular model used, and the inputs to the model • 5 -46 Actively traded, liquid contracts – Use market data Market values should reflect present values of expected future cash flows

Why Discounted Cash Flow Does Not Work Well for Valuing Options American: Can exercise anytime up to, and including expiration date European: Can exercise only on expiration date, but may be able to sell the option at current value Risk: Risk varies over time making DCF valuation ineffective 5 -47

GENERAL FEATURES OF OPTIONS ON FUTURES Option prices move in variable proportion to futures prices: Deep In-the-money . . . . Deep Out-of-the-money 5 -48 High proportion (almost one-to-one). . . . Low proportion (almost zero-to-one)

GENERAL FEATURES OF OPTIONS ON FUTURES • • Deltas are bounded between a minimum of zero and a maximum absolute value of one • 5 -49 Deltas increase as options move (deeper) in-themoney Time value is greatest for at-the-money options

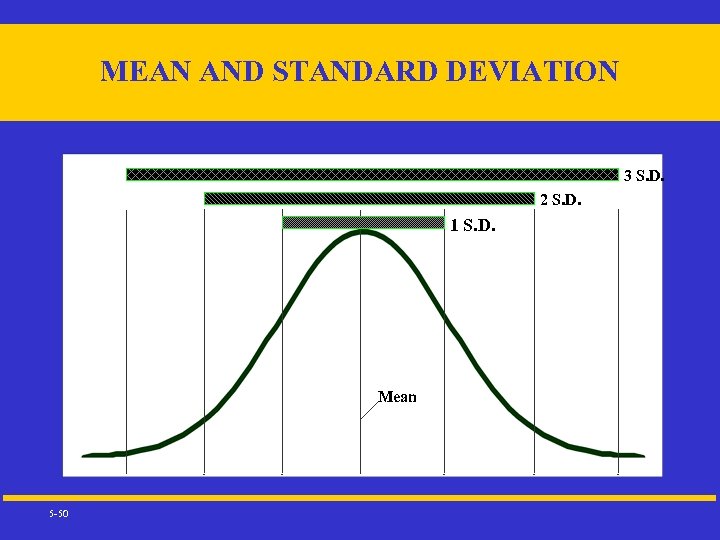MEAN AND STANDARD DEVIATION 3 S. D. 2 S. D. 1 S. D. Mean 5 -50

STANDARD DEVIATION • • 2 standard deviations is the range associated with a probability of 95. 4% • 5 -51 1 standard deviation is the range associated with a probability of 68. 3% 3 standard deviations is the range associated with a probability of 99. 7%

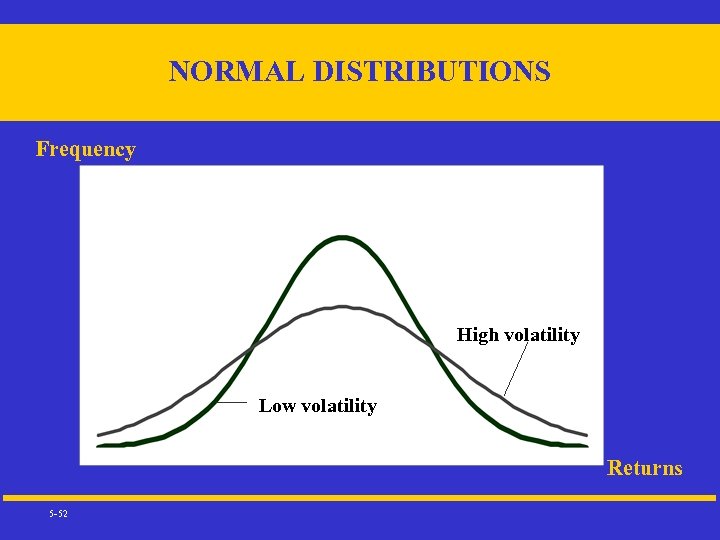NORMAL DISTRIBUTIONS Frequency High volatility Low volatility Returns 5 -52

STANDARD DEVIATION An Example If the standard deviation is 10%, that means. . . Probability 68. 3% within 10% (1 s. d. ) 95. 4% within 20% (2 s. d. ) 99. 7% 5 -53 Expected Price Change within 30% (3 s. d. )

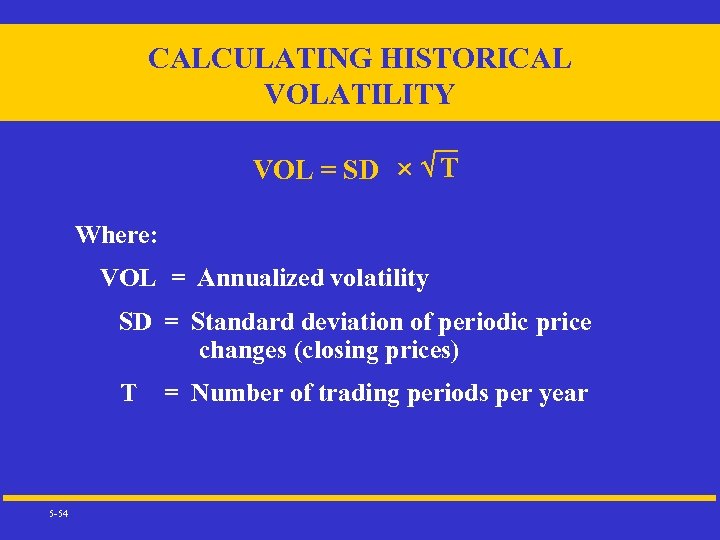CALCULATING HISTORICAL VOLATILITY VOL = SD T Where: VOL = Annualized volatility SD = Standard deviation of periodic price changes (closing prices) 5 -54 T = Number of trading periods per year

VOLATILITY EXAMPLE 24% Annual Volatility Daily SD = (24% 254) (24% 16) 1. 5% 68. 3% probability that overnight change +/- 1. 5% 95. 4% probability that overnight change +/- 3. 0% 99. 7% probability that overnight change +/- 4. 5% 5 -55

IMPLIED VOLATILITIES • • • Typically differ (significantly) from historical volatilities • 5 -56 Derived from current options prices Generally differ across strike prices and maturities Reflect probability distributions of forthcoming price changes (i. e. , the annualized standard deviations)

OPTION PRICE DETERMINANTS + + + – e Premium = f (IV, time, vol , r) • Intrinsic value (IV) • Time to expiration (time) e • Expected volatility (vol ) • Interest rates (r) The implied volatility of a “similar” option is the best input for expected volatility 5 -57

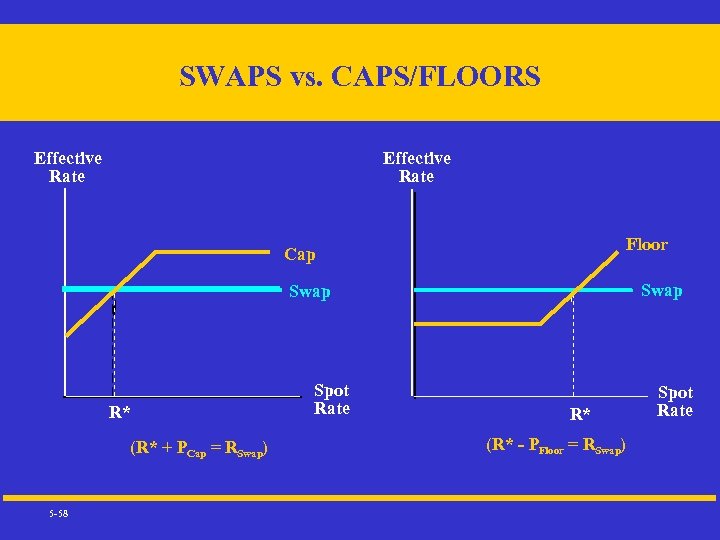SWAPS vs. CAPS/FLOORS Effective Rate Floor Cap Swap R* (R* + PCap = RSwap) 5 -58 Spot Rate R* (R* - PFloor = RSwap) Spot Rate

BUILDING CAPS • • • 5 -59 A cap is a series of individual options (caplets), each relating to a specific rate-setting date The price of a cap is the sum of caplet prices Option horizons (times to expiration) increase for successive rate-setting dates All else equal, longer-dated caplets are more expensive than shorter dated caplets Normal yield curves (i. e. , expectations of rising interest rates) inflate longer dated caplets, and vice versa

FORWARD RATES 10. 00% 7% Strike Yield 8. 00% 6. 00% 4. 00% 2. 00% 0. 00% 4 5 -60 8 12 16 20 24 Quarters 28 32 36 40

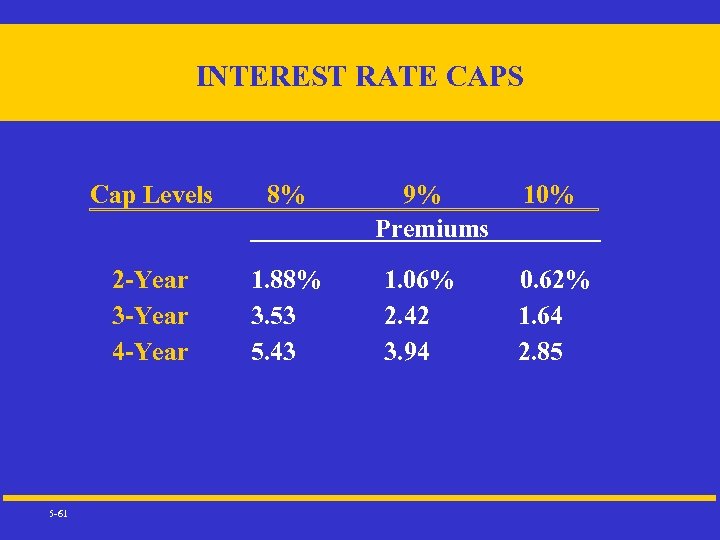INTEREST RATE CAPS Cap Levels 2 -Year 3 -Year 4 -Year 5 -61 8% 1. 88% 3. 53 5. 43 9% Premiums 1. 06% 2. 42 3. 94 10% 0. 62% 1. 64 2. 85

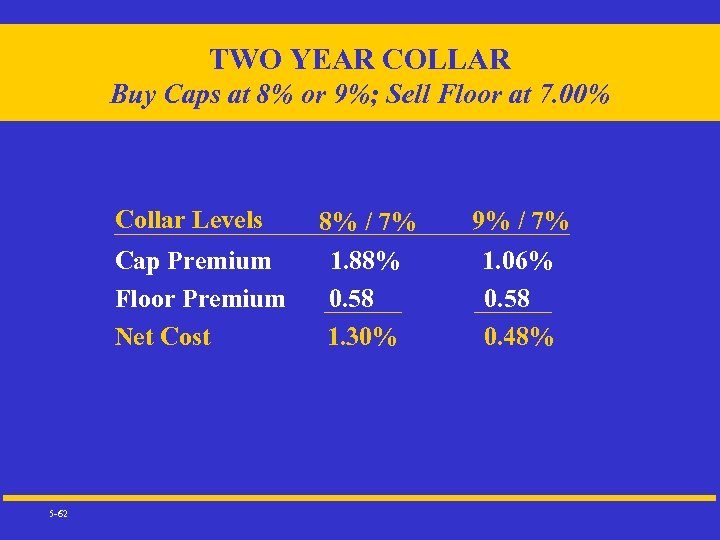TWO YEAR COLLAR Buy Caps at 8% or 9%; Sell Floor at 7. 00% Collar Levels Cap Premium Floor Premium Net Cost 5 -62 8% / 7% 1. 88% 0. 58 1. 30% 9% / 7% 1. 06% 0. 58 0. 48%

TWO YEAR CORRIDOR Buy Caps at 8% or 9%; Sell caps at 10. 00% Corridor Levels 8% / 10% Long Cap Premium 1. 88% Short Cap Premium 0. 62 Net Cost 1. 26% 5 -63 9% / 10% 1. 06% 0. 62 0. 44%

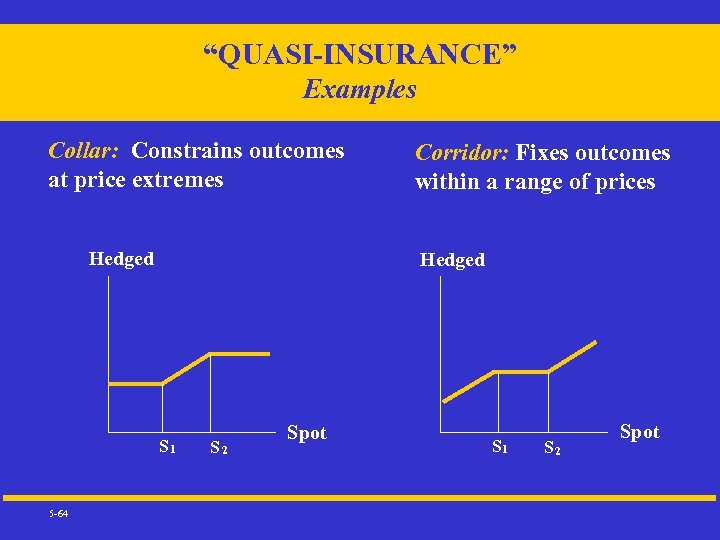“QUASI-INSURANCE” Examples Collar: Constrains outcomes at price extremes Hedged S 1 5 -64 Corridor: Fixes outcomes within a range of prices S 2 Spot S 1 S 2 Spot

New Example Coming Up 5 -65

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase • On 1/1/X 1, XYZ forecasts a 12/31/X 1 purchase of $100 million 5 -year 6% Treasury notes to be classified AFS • At 1/1/X 1 the 1 -year forward rate for 5 -year Treasury notes is 6 % • XYZ wants to lock in at least the 6% yield for the $100 million Treasury note purchase • XYZ’s hedge strategy is to purchase a call option on $100 million of the 5 -year Treasury notes that have a 6% 1 -year forward rate 5 -66

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase • • The American call option purchased at 1/1/X 1 has a 1 -year term • 5 -67 XYZ specified that hedge effectiveness will be measured based on the total price change of the Treasury notes and the intrinsic value of the option (zero at 1/1/X 1) The call premium is $1. 4 million, the strike rate is 6%, and the option is currently at-themoney

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase On 1/1/X 1, the following activity is recorded: Call option asset Cash 1, 400, 000 To record the option purchase 5 -68 1, 400, 000

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase At 6/30/X 1, the 12/31 X 1 forward 5 -year Treasury rate has declined 100 basis points from 6% to 5% and the market price is 104. 376. The following entry is recorded to reflect the increase in the call option’s intrinsic value. Call option asset OCI 4, 376, 000 To record the call option’s intrinsic value (assuming a price of 104. 376, calculated as $500, 000 annuity received for 10 semiannual periods discounted at 5% = $4, 376, 000). 5 -69

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase (continued) At 6/30/X 1, XYZ also determines that the call option’s time value has decreased Earnings Call option asset 800, 000 To record call option’s time value decrease 5 -70

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase At 12/31/X 1, XYZ exercises the option and takes delivery of the Treasury notes: Earnings 600, 000 Call option asset To write off option time value balance Treasury notes 100, 000 Cash Treasury notes (premium) 4, 376, 000 Call option asset To record exercise of option 5 -71 600, 000 100, 000 4, 376, 000

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase • • The $4, 376, 000 Treasury note premium is amortized over the life of the bond and offsets the above OCI impact. • 5 -72 The 12/31/X 1 OCI balance of $4, 376, 000 is reclassified into earnings over the life of the bond. The interest method is used to calculate the periodic amount reclassified into earnings. On a cash flow and earnings basis, XYZ succeeded in locking in a minimum 6% return on the Treasury notes as if these were purchased at par.

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase XYZ demonstrates that the hedge was effective as follows: Price of a 6% bond purchased in a 5% rate environment $104, 376, 000 Less call option proceeds (4, 376, 000) Net price 5 -73 $100, 000

CASE 7 - Cash Flow Hedge of Forecasted Treasury Note Purchase If XYZ sold the $100 million bond on 6/30/X 2, the remaining OCI balance is reclassified into earnings because the hedged item no longer affects earnings. 5 -74

New Example Coming Up 5 -75

CASE 8 Fair Value Hedge of AFS Security • XYZ owns 1, 000 shares of ABC worth $100 each ($100, 000) • • XYZ wants to hedge downside price risk • Effectiveness is measured by comparing decreases in fair value of investment with intrinsic value of option 5 -76 On 1/1/X 1, XYZ purchases an at-the-money put option on 1, 000 ABC shares expiring in 6 months; exercise price is $100; option premium is $15, 000

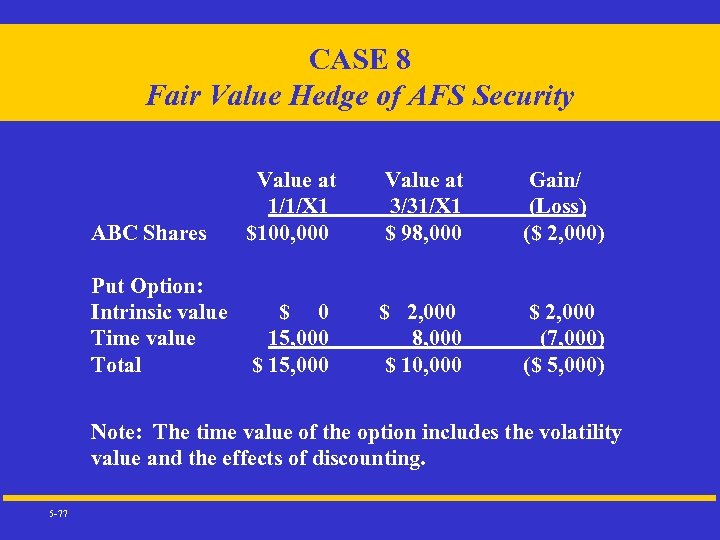CASE 8 Fair Value Hedge of AFS Security ABC Shares Value at 1/1/X 1 $100, 000 Put Option: Intrinsic value $ 0 Time value 15, 000 Total $ 15, 000 Value at 3/31/X 1 $ 98, 000 Gain/ (Loss) ($ 2, 000) $ 2, 000 8, 000 $ 10, 000 $ 2, 000 (7, 000) ($ 5, 000) Note: The time value of the option includes the volatility value and the effects of discounting. 5 -77

CASE 8 Fair Value Hedge of AFS Security Journal entry at 1/1/X 1 Option Contract Cash 15, 000 To record payment of option premium No journal entry for hedged item 5 -78

CASE 8 Fair Value Hedge of AFS Security Journal entries at 3/31/X 1 Earnings Investment in ABC 2, 000 To record loss on investment in ABC Earnings (time value) Option contract Earnings (intrinsic value) To record activity up to 3/31/X 1 5 -79 7, 000 5, 000 2, 000