Optimizing Sensing from Water to the Web Andreas

Optimizing Sensing from Water to the Web Andreas Krause rsrg@caltech. . where theory and practice collide

Monitoring algal blooms Algal blooms threaten freshwater 4 million people without water 1300 factories shut down $14. 5 billion to clean up Other occurrences in Australia, Japan, Canada, Brazil, Mexico, Great Britain, Portugal, Germany … Growth processes still unclear Need to characterize growth in the lakes, not in the lab! Tai Lake China 10/07 MSNBC 2

Monitoring rivers and lakes [IJCAI ‘ 07] Need to monitor large spatial phenomena Temperature, nutrient distribution, fluorescence, … NIMS Kaiser et. al. (UCLA) Can only make a limited number of measurements! Depth Color indicates actual temperature Predicted temperature Use robotic sensors to cover large areas Predict at unobserved locations Location across lake Where should we sense to get most accurate predictions? 3

Monitoring water networks [J Wat Res Mgt 2008] Contamination of drinking water could affect millions of people Contamination Sensors Simulator from EPA Hach Sensor Place sensors to detect contaminations ~$14 K “Battle of the Water Sensor Networks” competition Where should we place sensors to quickly detect contamination? 4

Sensing problems Want to learn something about the state of the world Estimate water quality in a geographic region, detect outbreaks, … We can choose (partial) observations… Make measurements, place sensors, choose experimental parameters … … but they are expensive / limited hardware cost, power consumption, grad student time … Want to cost-effectively get most useful information! Fundamental problem in Machine Learning: How do we decide what to learn from? 5

Related work Sensing problems considered in Experimental design (Lindley ’ 56, Robbins ’ 52…), Spatial statistics (Cressie ’ 91, …), Machine Learning (Mac. Kay ’ 92, …), Robotics (Sim&Roy ’ 05, …), Sensor Networks (Zhao et al ’ 04, …), Operations Research (Nemhauser ’ 78, …) Existing algorithms typically Heuristics : No guarantees! Can do arbitrarily badly. Find optimal solutions (Mixed integer programming, POMDPs): Very difficult to scale to bigger problems. 6

Contributions Theoretical: Approximation algorithms that have theoretical guarantees and scale to large problems Applied: Empirical studies with real deployments and large datasets 7

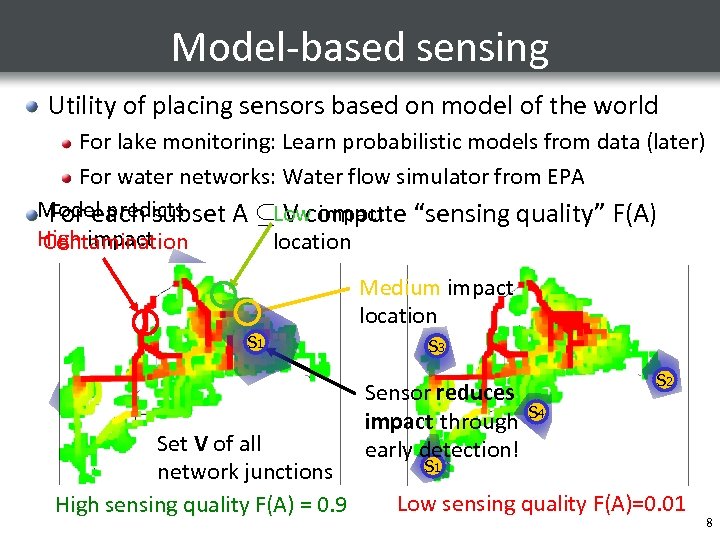
Model-based sensing Utility of placing sensors based on model of the world For lake monitoring: Learn probabilistic models from data (later) For water networks: Water flow simulator from EPA Model predicts For each subset A µLow impact “sensing quality” F(A) V compute High impact Contamination location Medium impact location S 3 S 1 2 S S 1 S 4 Set V of all network junctions High sensing quality F(A) = 0. 9 S 3 Sensor reduces impact through early detection! S 2 S 4 S 1 Low sensing quality F(A)=0. 01 8

Optimizing sensing / Outline Sensing locations Sensing quality Sensing cost Sensing budget Sensor placement Robust sensing Complex constraints Sequential sensing 9

Sensor placement Given: finite set V of locations, sensing quality F Want: A*µ V such that S 3 Typically NP-hard! Greedy algorithm: S 2 S 1 S 5 S 4 S 6 Start with A = ; For i = 1 to k s* : = argmaxs F(A [ {s}) A : = A [ {s*} How well can this simple heuristic do? 10

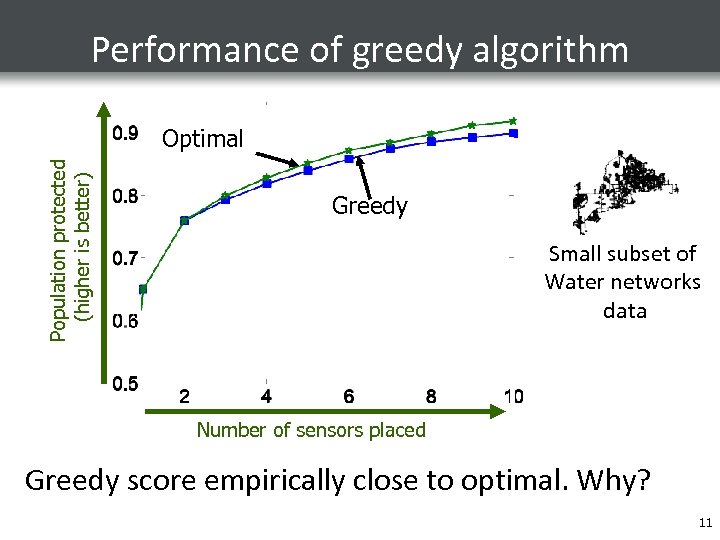
Performance of greedy algorithm Population protected (higher is better) Optimal Greedy Small subset of Water networks data Number of sensors placed Greedy score empirically close to optimal. Why? 11

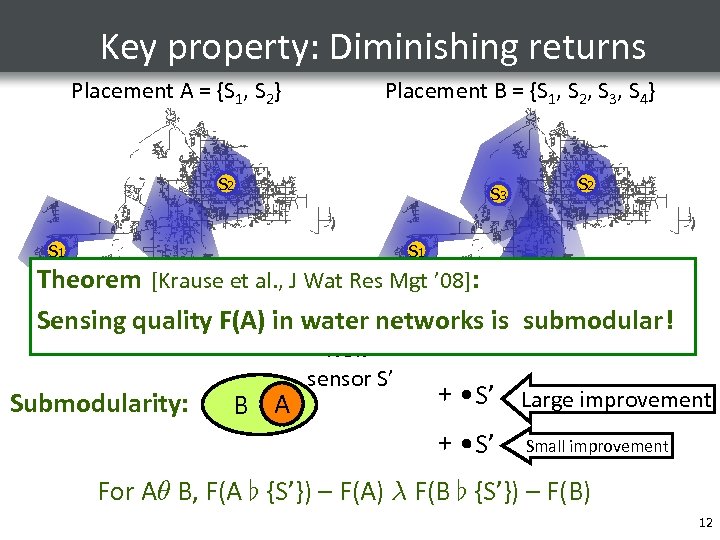
Key property: Diminishing returns Placement A = {S 1, S 2} Placement B = {S 1, S 2, S 3, S 4} S 2 S 3 S 1 S 4 Theorem [Krause et al. , J Wat Res Mgt ’ 08]: Adding S’ S’ Sensing quality. S’F(A) in water networks is submodular! will help a lot! Submodularity: B A New sensor S’ doesn’t help much + S’ Large improvement + S’ Small improvement For Aµ B, F(A [ {S’}) – F(A) ¸ F(B [ {S’}) – F(B) 12

One reason submodularity is useful Theorem [Nemhauser et al ‘ 78] Greedy algorithm gives constant factor approximation F(Agreedy) ¸ (1 -1/e) F(Aopt) ~63% Greedy algorithm gives near-optimal solution! Guarantees best possible unless P = NP! Many more reasons, sit back and relax… 13

Building a Sensing Chair [UIST ‘ 07] People sit a lot Activity recognition in assistive technologies Seating pressure as user interface Equipped with 1 sensor per cm 2! Costs $16, 000! Lean Slouch left forward Can we get similar accuracy with fewer, 82% accuracy on cheaper sensors? 10 postures! [Tan et al] 14

How to place sensors on a chair? Sensor readings at locations V as random variables Predict posture Y using probabilistic model P(Y, V) Pick sensor locations A* µ V to minimize entropy: Possible locations V Placed sensors, did a user study: Theorem: Information gain Accuracy Cost is submodular!* [UAI’ 05] Before After 82% 79% $16, 000 $100 Similar accuracy at <1% of the cost! *See store for details 15

Battle of the Water Sensor Networks Competition Real metropolitan area network (12, 527 nodes) Water flow simulator provided by EPA 3. 6 million contamination events Multiple objectives: Detection time, affected population, … Place sensors that detect well “on average” 16

BWSN Competition results [Ostfeld et al. , J Wat Res Mgt 2008] 13 participants Performance measured in 30 different criteria G: Genetic algorithm D: Domain knowledge E: “Exact” method (MIP) H: Other heuristic G H E G G H 25 E 20 15 10 5 & h ac pr o do ll Gu an et. a Hu El l. an ia de g s et &. a Po l. ly ca Pr rp op ou at Os o & tfe Pi ld lle & r Sa lo m on W s u & W al sk Do i rin ie t. al Be. rr O y et ur ap. al. Ba ac Tr rk m el an i 0 Gu ld tfe Os & D G H D G ht Total Score Higher is better 30 ire im Gh Pr ei s 24% better performance than runner-up! 17

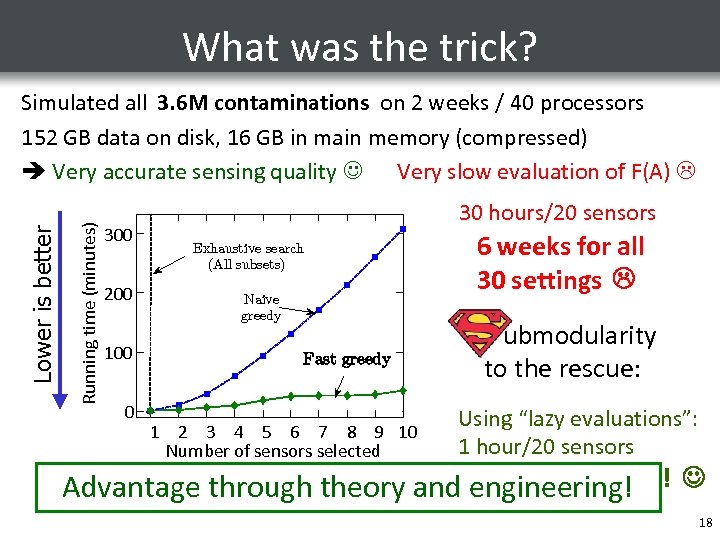
What was the trick? Running time (minutes) Lower is better Simulated all 3. 6 M contaminations on 2 weeks / 40 processors 152 GB data on disk, 16 GB in main memory (compressed) Very accurate sensing quality Very slow evaluation of F(A) 300 200 100 0 30 hours/20 sensors 6 weeks for all 30 settings Exhaustive search (All subsets) Naive greedy Fast greedy 1 2 3 4 5 6 7 8 9 10 Number of sensors selected ubmodularity to the rescue: Using “lazy evaluations”: 1 hour/20 sensors Advantage through theory and. Done after 2 days! engineering! 18

What about worst-case? Knowing the sensor locations, an adversary contaminates here! S 3 S 2 S 1 S 3 S 2 S 4 S 1 Placement detects Very different average-case impact, well on “average-case” Same worst-case impact (accidental) contamination Where should we place sensors to quickly detect in the worst case? 19

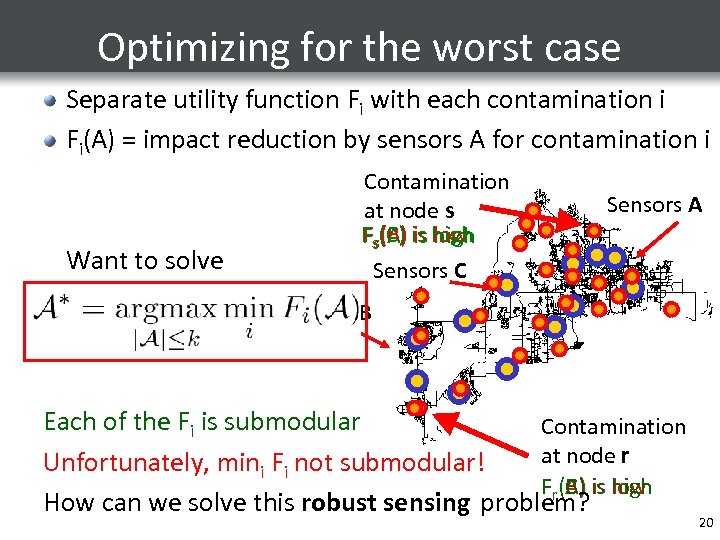
Optimizing for the worst case Separate utility function Fi with each contamination i Fi(A) = impact reduction by sensors A for contamination i Want to solve Contamination at node s Fs(C) is high (B) (A) low Sensors C Sensors A Sensors B Each of the Fi is submodular Contamination at node r Unfortunately, mini Fi not submodular! Fr(A) is high (C) (B) low How can we solve this robust sensing problem? 20

Outline Sensor placement Robust sensing Complex constraints Sequential sensing 21

How does the greedy algorithm do? V={ , , } Can only buy k=2 Optimal solution Optimal score: 1 Set A F 1 1 0 F 2 0 2 mini Fi 0 0 Hence we can’t find any 1 approximation algorithm. 2 Or 1 can 2 1 we? Greedy picks first Then, can choose only or Greedy score: Greedy does arbitrarily badly. Is there something better? Theorem [NIPS ’ 07]: The problem max|A|· k mini Fi(A) does not admit any approximation unless P=NP 22

Alternative formulation If somebody told us the optimal value, can we recover the optimal solution A*? Need to find Is this any easier? Yes, if we relax the constraint |A| · k 23

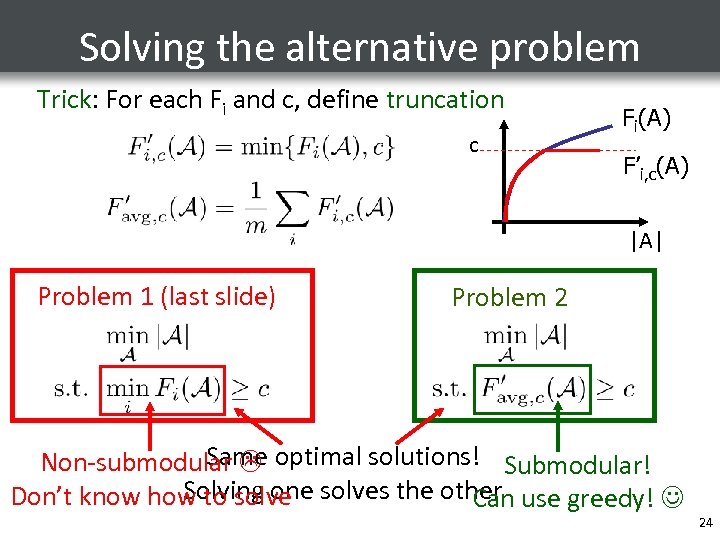
Solving the alternative problem Trick: For each Fi and c, define truncation c Fi(A) F’i, c(A) |A| Problem 1 (last slide) Problem 2 Same Non-submodular optimal solutions! Submodular! Solving one Don’t know how to solves the other use greedy! Can 24

Back to our example Set A F 1 1 0 F 2 0 2 mini Fi 0 0 F’avg, 1 1 (1+ )/2 2 1 Guess c=1 First pick Then pick Optimal solution! 2 1 1 ½ ½ (1+ )/2 How do we find c? Do binary search! 25

Saturate Algorithm [NIPS ‘ 07] Given: set V, integer k and submodular functions F 1, …, Fm Initialize cmin=0, cmax = mini Fi(V) Do binary search: c = (cmin+cmax)/2 Greedily find AG such that F’avg, c(AG) = c If |AG| · k: increase cmin If |AG| > k: decrease cmax until convergence Truncation threshold (color) 26

Theoretical guarantees Theorem: The problem max|A|· k mini Fi(A) does not admit any approximation unless P=NP Theorem: Saturate finds a solution AS such that mini Fi(AS) ¸ OPTk and |AS| · k where OPTk = max|A|·k mini Fi(A) = 1 + log maxs Fi({s}) i Theorem: If there were a polytime algorithm with better factor < , then NP µ DTIME(nlog n) 27

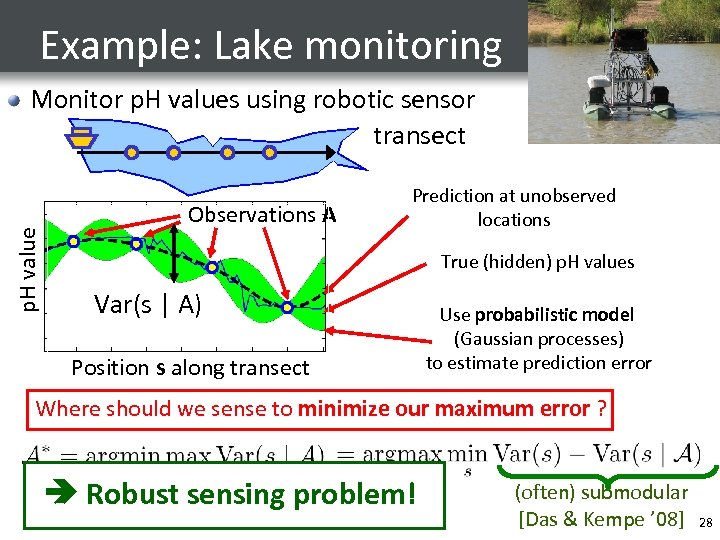
Example: Lake monitoring p. H value Monitor p. H values using robotic sensor transect Observations A Prediction at unobserved locations True (hidden) p. H values Var(s | A) Position s along transect Use probabilistic model (Gaussian processes) to estimate prediction error Where should we sense to minimize our maximum error ? Robust sensing problem! (often) submodular [Das & Kempe ’ 08] 28

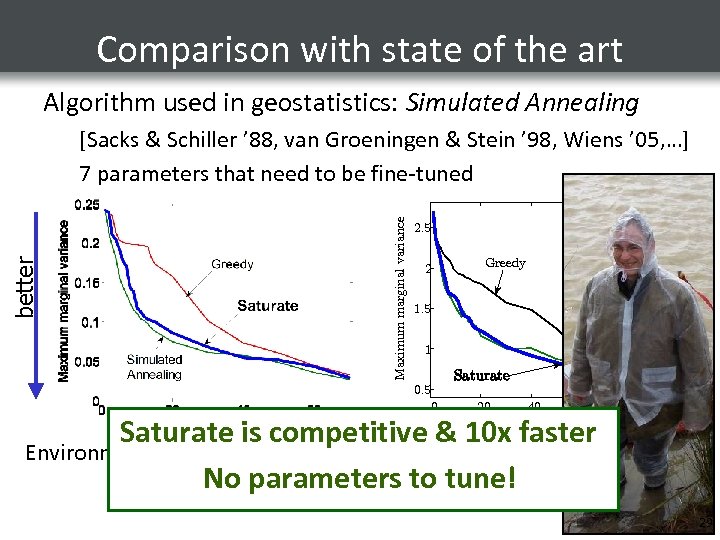
Comparison with state of the art Algorithm used in geostatistics: Simulated Annealing Maximum marginal variance better [Sacks & Schiller ’ 88, van Groeningen & Stein ’ 98, Wiens ’ 05, …] 7 parameters that need to be fine-tuned 2. 5 2 Greedy 1. 5 Simulated Annealing 1 0. 5 0 Saturate 20 40 60 Number of sensors Saturate is competitive & 10 x faster Precipitation data Environmental monitoring No parameters to tune! 80 100 29

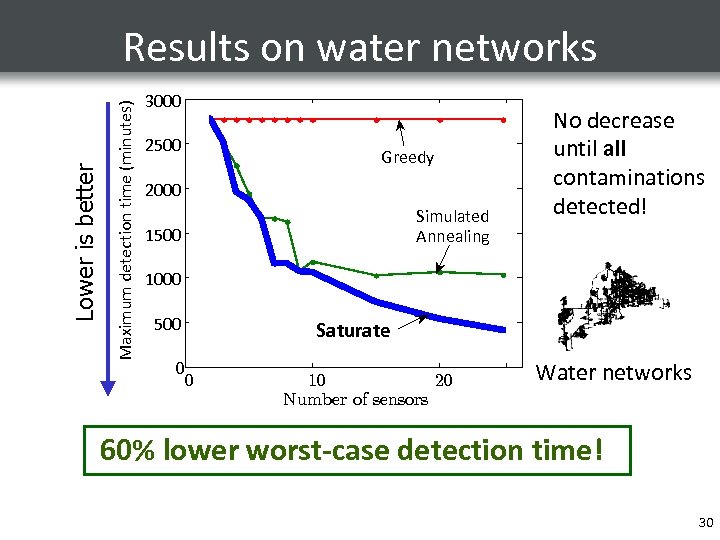
Maximum detection time (minutes) Lower is better Results on water networks 3000 2500 Greedy 2000 Simulated Annealing 1500 No decrease until all contaminations detected! 1000 500 0 Saturate 0 10 20 Number of sensors Water networks 60% lower worst-case detection time! 30

Outline Sensor placement Robust sensing Complex constraints Sequential sensing 31

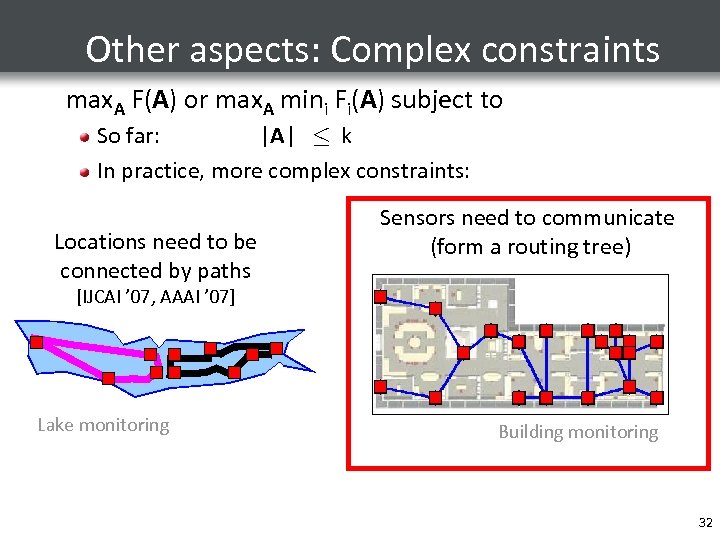
Other aspects: Complex constraints max. A F(A) or max. A mini Fi(A) subject to So far: |A| · k In practice, more complex constraints: Locations need to be connected by paths Sensors need to communicate (form a routing tree) [IJCAI ’ 07, AAAI ’ 07] Lake monitoring Building monitoring 32

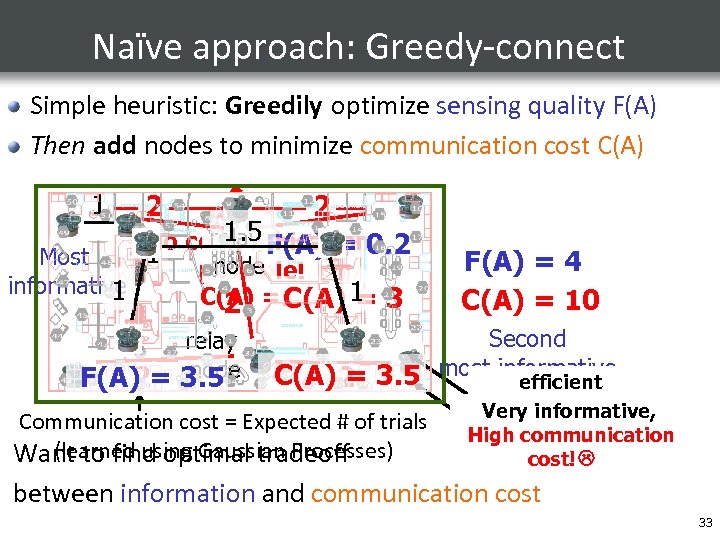
Naïve approach: Greedy-connect Simple heuristic: Greedily optimize sensing quality F(A) Then add nodes to minimize communication cost C(A) 1 Most informative 11 2 1. 5 relay F(A) = No communication 0. 2 1 2 node possible! C(A) = 1 C(A) 1 3 = 2 relay 2 node F(A) = 3. 5 F(A) = 4 C(A) = 10 Second C(A)2 3. 5 most informative = efficient Communication cost = Expected # of trials (learned using Gaussian Processes) Want to find optimal tradeoff communication! Very informative, High Not very communication informative cost! between information and communication cost 33

The p. SPIEL Algorithm p. SPIEL: [IPSN ’ 06 – Best Paper Award] padded Sensor Placements at Informative and cost-Effective Locations Theorem: p. SPIEL finds a placement A with sensing quality F(A) ¸ (1) OPTF communication cost C(A) · O(log |V|) OPTC Real deployment at CMU Architecture department 44% lower error and 19% lower communication cost than placement by domain expert! 34

Outline Sensor placement Robust sensing Complex constraints Sequential sensing 35

Other aspects: Sequential sensing You walk up to a lake, but don’t have a model Want sensing locations to learn the model (explore) and predict well (exploit) Chosen locations depend on measurements! [ICML ’ 07] Exploration—Exploitation analysis for Active Learning in Gaussian Processes 36

Summary so far Submodularity in All thesesensing optimization physical sensing. applications involve Now Greedy is near-optimal [UAI ’ 05, JMLR ’ 07, completely for something KDD ’ 07] different. Let’s jump from water… planning Path Robust sensing Communication constraints Greedy fails badly Saturate is near-optimal [NIPS ’ 07] Constrained submodular optimization p. SPIEL gives strong guarantees [IJCAI ’ 07, IPSN ’ 06, AAAI ‘ 07] Sequential sensing Exploration Exploitation Analysis [ICML ’ 07, IJCAI ‘ 05] 37

… to the Web! You have 10 minutes each day for reading blogs / news. Which of the million blogs should you read? 38

Cascades in the Blogosphere Time [KDD 07 – Best Paper Award] Learn about story after us! Information cascade Which blogs should we read to learn about big cascades early? 39

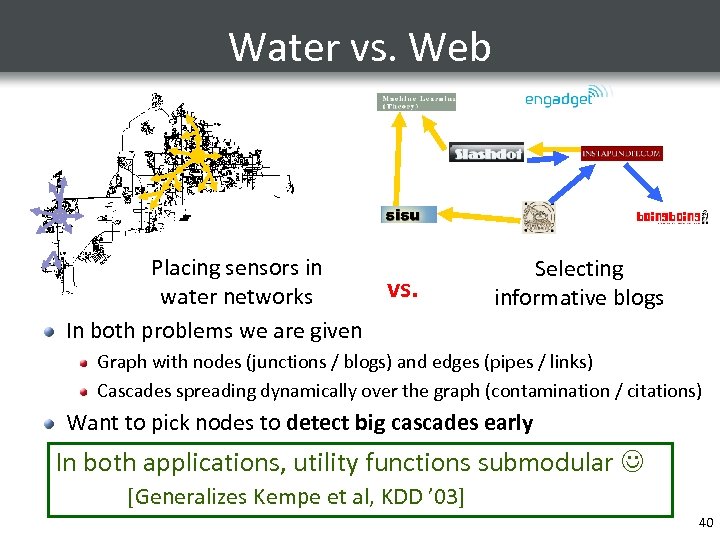
Water vs. Web Placing sensors in water networks In both problems we are given vs. Selecting informative blogs Graph with nodes (junctions / blogs) and edges (pipes / links) Cascades spreading dynamically over the graph (contamination / citations) Want to pick nodes to detect big cascades early In both applications, utility functions submodular [Generalizes Kempe et al, KDD ’ 03] 40

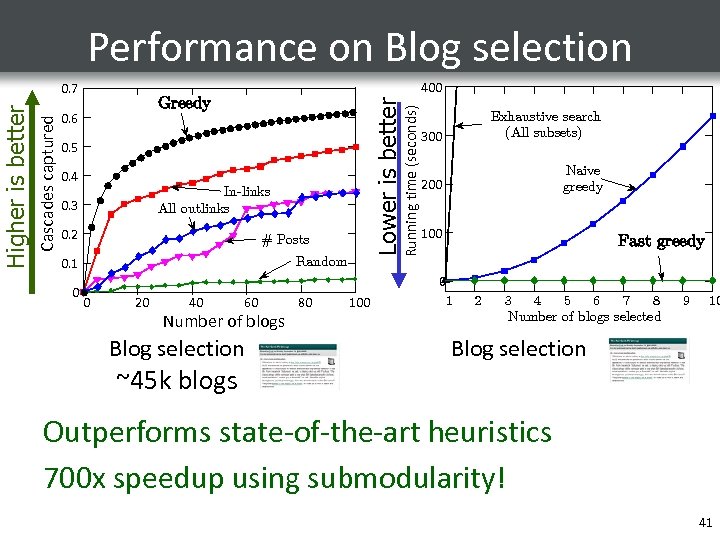
0. 7 400 Greedy Running time (seconds) 0. 6 Lower is better Cascades captured Higher is better Performance on Blog selection 0. 5 0. 4 In-links All outlinks 0. 3 0. 2 # Posts 0. 1 0 Random 0 20 40 60 Number of blogs Blog selection ~45 k blogs 80 100 300 Exhaustive search (All subsets) 200 Naive greedy 100 Fast greedy 0 1 2 3 4 5 6 7 8 Number of blogs selected 9 10 Blog selection Outperforms state-of-the-art heuristics 700 x speedup using submodularity! 41

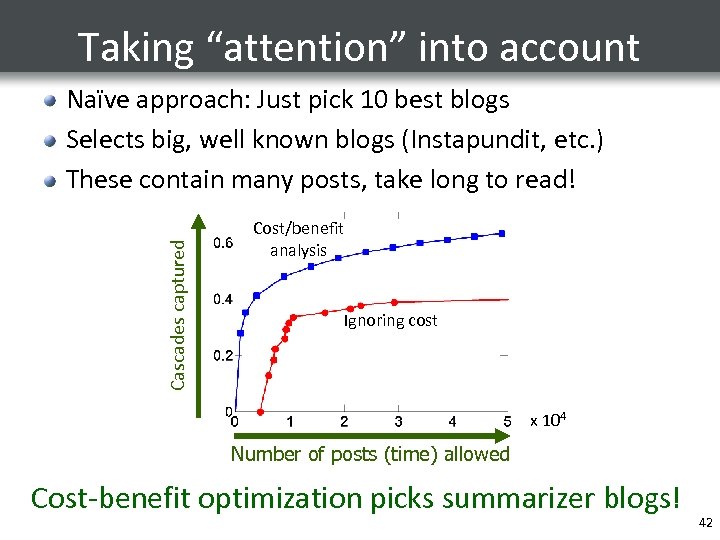
Taking “attention” into account Cascades captured Naïve approach: Just pick 10 best blogs Selects big, well known blogs (Instapundit, etc. ) These contain many posts, take long to read! Cost/benefit analysis Ignoring cost x 104 Number of posts (time) allowed Cost-benefit optimization picks summarizer blogs! 42

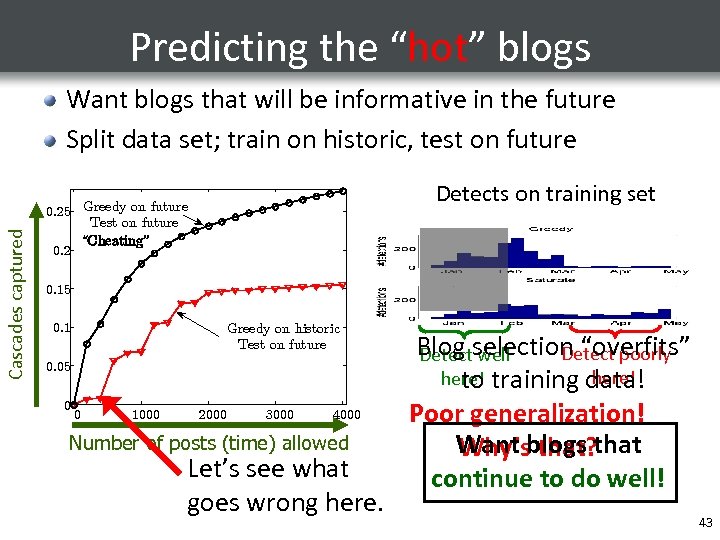
Predicting the “hot” blogs Cascades captured Want blogs that will be informative in the future Split data set; train on historic, test on future Detects on training set 0. 25 Greedy on future Test on future “Cheating” 0. 2 0. 15 0. 1 Greedy on historic Test on future 0. 05 0 0 1000 2000 3000 4000 Number of posts (time) allowed Let’s see what goes wrong here. Blog selection “overfits” Detect poorly Detect well here! training data! to Poor generalization! Want blogs that Why’s that? continue to do well! 43

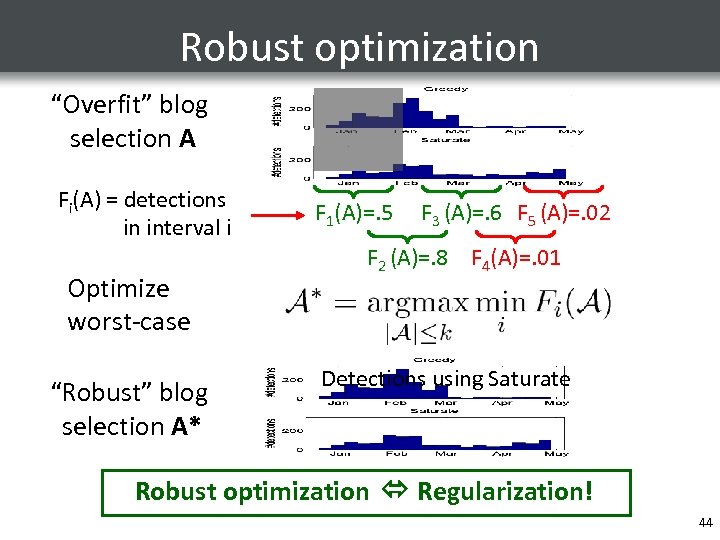
Robust optimization “Overfit” blog selection A Fi(A) = detections in interval i Optimize worst-case “Robust” blog selection A* F 1(A)=. 5 F 3 (A)=. 6 F 5 (A)=. 02 F 2 (A)=. 8 F 4(A)=. 01 Detections using Saturate Robust optimization Regularization! 44

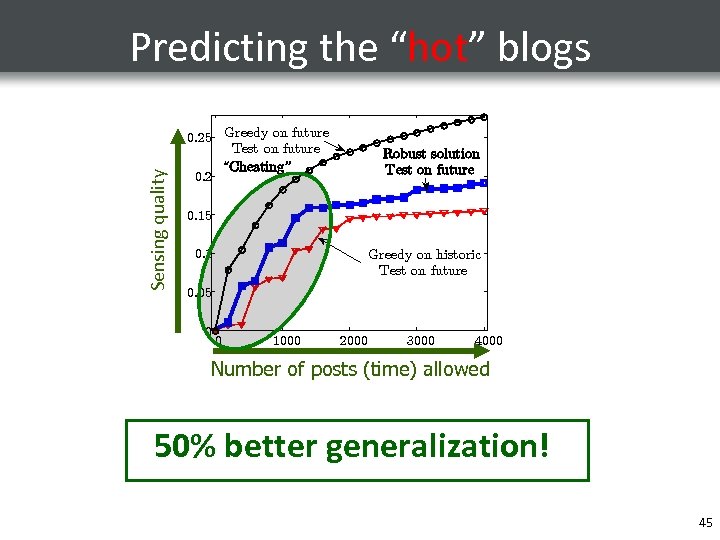
Sensing quality Predicting the “hot” blogs 0. 25 Greedy on future Test on future “Cheating” 0. 2 Robust solution Test on future 0. 15 0. 1 Greedy on historic Test on future 0. 05 0 0 1000 2000 3000 4000 Number of posts (time) allowed 50% better generalization! 45

Future work Submodularity in sensing optimization Greedy is near-optimal [UAI ’ 05, JMLR ’ 07, KDD ’ 07] Robust sensing Greedy fails badly Robust optimization Saturate is near-optimal better [NIPS ’ 07] generalization Path planning Communication constraints Constrained submodular optimization Constrained optimization p. SPIEL gives strong guarantees better use of “attention” [IJCAI ’ 07, IPSN ’ 06] Thesis in a box Sequential sensing Exploration Exploitation Analysis [ICML ’ 07] 46

Future work Algorithmic and statistical machine learning UAI ‘ 05 Fundamental questions in Information Acquisition ICML ‘ 06 and Sensys ‘ 05 Interpretation ISWC ‘ 06 Machine learning and sensing in natural sciences and engineering Trans Mob Comp ‘ 06 Machine learning and optimization on the web Thesis in a box 47

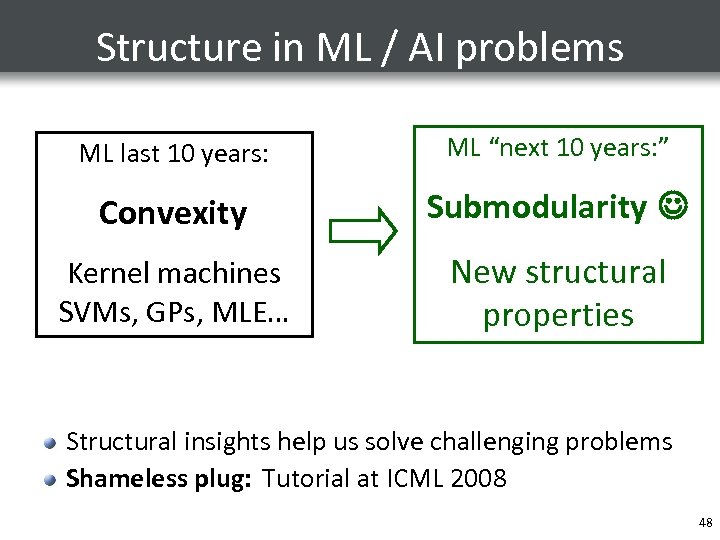
Structure in ML / AI problems ML last 10 years: ML “next 10 years: ” Convexity Submodularity Kernel machines SVMs, GPs, MLE… New structural properties Structural insights help us solve challenging problems Shameless plug: Tutorial at ICML 2008 48

Future work Algorithmic and statistical machine learning Fundamental questions in Information Acquisition and Interpretation Machine learning and sensing in natural sciences and engineering Machine learning and optimization on the web Thesis in a box 49

Fundamental bottlenecks in information acquisition Attention Web extremely scarce, non-renewable! User Privacy Preliminary results Utility/Privacy in Personalized search. Submodularity is key! Planned study: data from 2 million blogs from spinn 3 r. com 50

www. blogcascades. org 5 months, 2 million blogs, 55 million posts 51

Future work Algorithmic and statistical machine learning Fundamental questions in Information Acquisition and Interpretation Machine learning and sensing in natural sciences and engineering Machine learning and optimization on the web Thesis in a box 52

Machine learning for natural sciences Large, distributed research efforts Multiple research teams Multiple sensing modalities Need to integrate experimental results Reason about noisy measurements + scientific hypotheses Key problem in AI / ML: [Oßwald et al, Lasser et al] [Mac. Intyre et al, Singh et al] Integrate noisy sensor data and symbolic, domain knowledge New approaches toward autonomous science 53

Future work Algorithmic and statistical machine learning Fundamental questions in Information Acquisition and Interpretation Machine learning and sensing in natural sciences and engineering Machine learning and optimization on the web Thesis in a box Many opportunities for collaboration! 54

Conclusions Sensing and information acquisition problems are important and ubiquitous Can exploit structure to find provably good solutions Presented algorithms with strong guarantees Perform well on real world problems Thanks to: Carlos Guestrin, Anupam Gupta, Jon Kleinberg, Eric Horvitz, Jure Leskovec, Ajit Singh, Amarjeet Singh, Vipul Singhvi, William Kaiser, Jeanne Van. Briesen, Christos Faloutsos, Brendan Mc. Mahan, Natalie Glance 55

56

Worst- vs. average case Given: Possible locations V, submodular functions F 1, …, Fm Average-case score Worst-case score Strong assumptions! Very pessimistic! Want to optimize both average- and worst-case score! Can modify Saturate to solve this problem! 57

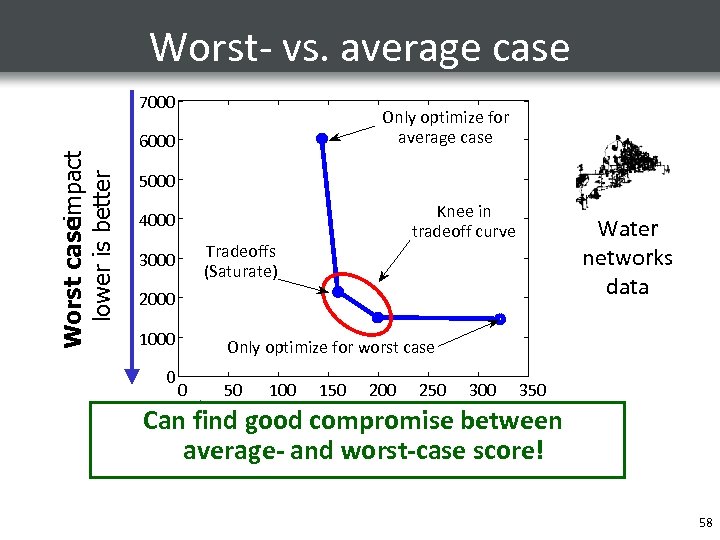
Worst- vs. average case Worst caseimpact lower is better 7000 Only optimize for average case 6000 5000 Knee in tradeoff curve 4000 Tradeoffs (Saturate) 3000 Water networks data 2000 1000 0 Only optimize for worst case 0 50 100 150 200 250 300 350 Can find Average case good compromise between impact average- and worst-case score! lower is better 58

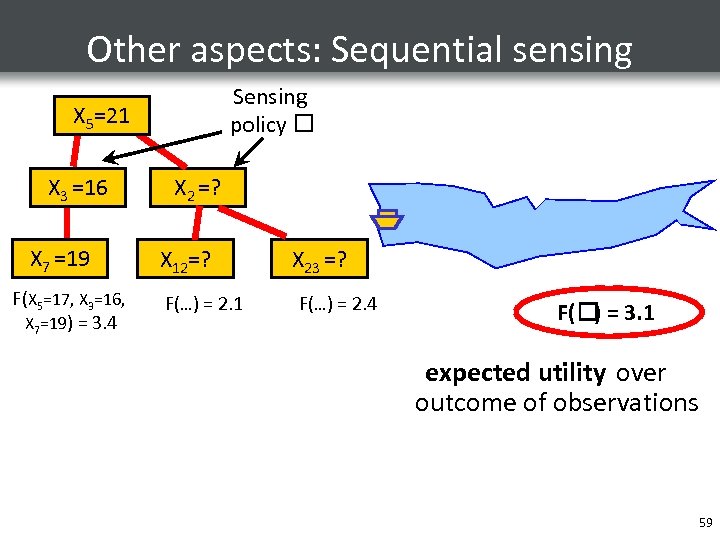
Other aspects: Sequential sensing Sensing policy X 55=? X =17 =21 X 33=16 X =? X 77=19 X =? F(X 5=17, X 3=16, X 7=19) = 3. 4 X 2 =? X 12=? F(…) = 2. 1 X 23 =? F(…) = 2. 4 F( = 3. 1 ) expected utility over outcome of observations 59

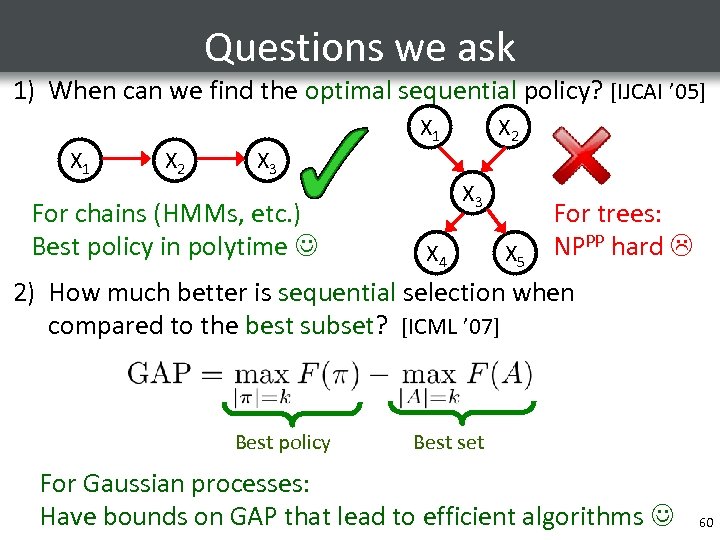
Questions we ask 1) When can we find the optimal sequential policy? [IJCAI ’ 05] X 1 X 2 X 3 For chains (HMMs, etc. ) Best policy in polytime X 2 X 3 X 4 X 5 For trees: NPPP hard 2) How much better is sequential selection when compared to the best subset? [ICML ’ 07] Best policy Best set For Gaussian processes: Have bounds on GAP that lead to efficient algorithms 60