Optimizing Customer Satisfaction By: Brian Murphy
Scenario Consumer has an income of $200 and wants to buy two fixed goods: hats and guns. Price of hats is $20 and price of shirts is $30. Consumer wants to buy a certain number of hats and shirts so that he spends all or nearly all of his income while optimizing his satisfaction.
Modeling Key Variables: ◦ ◦ ◦ Income (I) = $200 Number of Hats Purchased (H) Number of Shirts Purchased (S) Price of Hat (PH) = $20 Price of Shirt (PS) = $30 Income Equation: HPH + SPS = 200
Modeling In Microeconomics, consumer satisfaction is mathematically represented by a utility function. Utility function is usually generated from historical market trends. Most common utility function is of the form U=a. XαYβ For this problem, the consumer’s utility function is U(H, S) = 2 H 1/2 G 1/2
Finding the Optimal Bundle What we need to find optimum: ◦ Marginal Utility (MU) – the change in utility as a result of a small change in quantity of one good (calculated as the partial derivative of the utility function with respect to the good). ◦ Marginal Rate of Substitution (MRS) – utility gain from a small change in one good while the other good is held fixed (Calculated as the ratio of the two marginal utilities). ◦ Price ratio (PR) – ratio of the price of the two goods.
Finding the Optimal Bundle Calculated Variables: ◦ ◦ MUH = H-1/2 S 1/2 MUS = H 1/2 S-1/2 MRSH, S = MUH/ MUS = S/H PR = 20/30
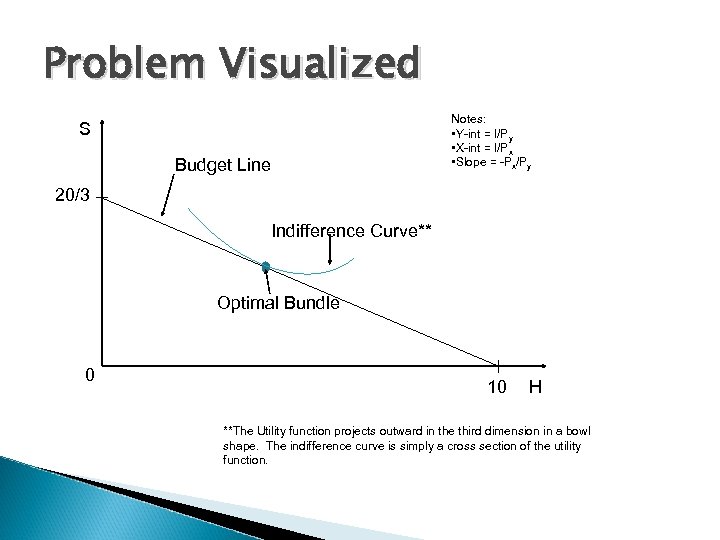
Problem Visualized S Budget Line Notes: • Y-int = I/Py • X-int = I/Px • Slope = -Px/Py 20/3 Indifference Curve** Optimal Bundle 0 10 H **The Utility function projects outward in the third dimension in a bowl shape. The indifference curve is simply a cross section of the utility function.
Solve At Optimal Bundle: ◦ Nearly all the money is spent ◦ Slope of Indifference Curve = Slope of Budget Line ◦ Slope of Indifference Curve = -MUH/ MUS = -MRSH, S Thus: S/H = 20/30, H = 1. 5 S Plug into Income Equation: 20(1. 5 s) + 30 s = 200 S* = 3. 33 H* = 1. 5 s* = 5
Скачать презентацию Optimizing Customer Satisfaction By Brian Murphy Scenario
b358a13ee57214d0e81828780e8cdea0.ppt