Optimization Schemes for Protective Jamming Swaminathan Sankararaman

Optimization Schemes for Protective Jamming • Swaminathan Sankararaman (Duke) • Karim Abu-Affash (Ben Gurion University, Israel) • Alon Efrat (me) (U Arizona, USA) • Sylvester David Eriksson-Bique (U Helsinki, Finland) • Valentin Polishchuk (U Helsinki, Finland) • Srinivasan Ramasubramanian (U Arizona, USA) • Michael Segal (Ben Gurion University, Israel) 1

RFID Devices • Tags and Readers • Sensitive information – Credit cards, patient information in hospitals, etc. – Tricky to encrypt due to severely limited capabilities 2

Eavesdroppers and Jammers • RFID tags (or other active wireless sources), are placed in storage areas. • The storage is surrounded by a fence • Hostile eavesdroppers might be present outside fence. • Idea for protection: Place (friendly) jammers that create "enough" noise to prevent successful unfriendly reading. • This jamming should not disturb legit reading within storage. fence e j j e j storage j s j e e Questions: 1. How to model successful jamming ? 2. Where to place jammers ? 3. Power assignments ? 4. How to orient antennas (if not omnidirectional) ? 5. How to schedule jammers (eg when battery operated) 3

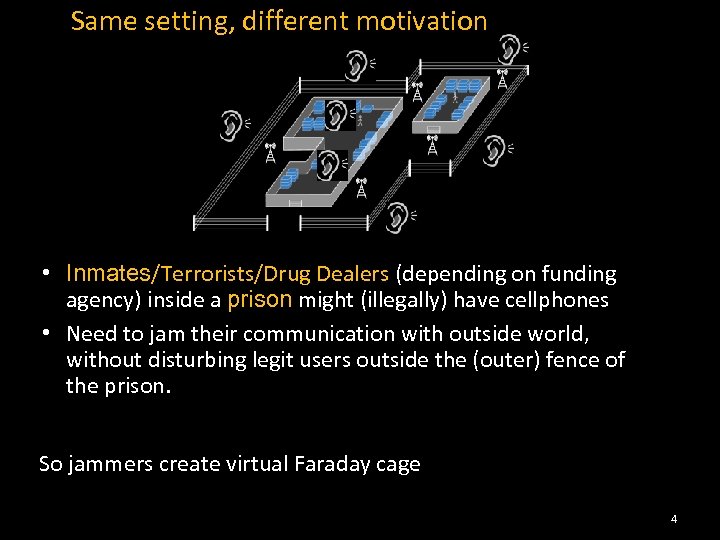Same setting, different motivation • Inmates/Terrorists/Drug Dealers (depending on funding agency) inside a prison might (illegally) have cellphones • Need to jam their communication with outside world, without disturbing legit users outside the (outer) fence of the prison. So jammers create virtual Faraday cage 4

Same setting, yet another motivation • Sensors communicate inside a sensors field. • Eavesdropper outside the fenced region try to decrepit the sensor communications. • Friendly jammers provide another level of security, on top of encryption. 5

Assumptions 1. 2. t 1 t 2 Only single frequency 3. No assumption about sensitivity of readers and eavesdroppers. Eavesdroppers could be anywhere outside fenced region. => No assumptions about range of tags and jammers. 4. 5. 6. No co-transmissions from tags. Jammers have no sensing abilities. Other source of noise are not taken into account in SINR model (only simplify the problem)

Successful Jamming p 3 p 2 t 1 Def: Given user-specified thresholds P 0 , δ 0 jamming is successful if: ①For every point ti inside the storage, the summed power from all jammers < P 0. ②For every point pi outside the fence (possible eavesdropper), and every placement of RFID tag ti, we have p 1 Power received = power transmitted / distance 2 Observation: For every eavesdropper q, need to worry only about nearest storage point (in omnidirectional case) Claim: Under “reasonable” assumption, enough to validate conditions only for points on boundaries of fence and storage (jammers could be placed anywhere, though)

Discretization, Witness Points and ILP p 1 p 2 t 1 j 3 We could discretize the fence and storage boundaries by placing a set W of “witness points”, and validate the conditions only on these points. For every storage witness point For every fence witness point Conclusions: Can use ILP to `solve’ variants of the problem such as • Picking a subsets of jammers from candidate locations • Schedule activation/deactivation of jammers activate to last longer. PROBLEM: • Running time depends critically on #constraints, so could not use too many witness points. So challenging to provide guarantees for non-witness points. New Result: • Can place only O(n/ε log (perimeter) ) witness points so successful is guaranteed everywhere, with ε-approximation of constants P 0 , δ 0

Directional eavesdropper • Eavesdropper could try to avoid the noise from Jammers by using directional antenna • Jamming problem now is to verify that for every placement and orientation of cone, successful jamming is obtained when considering only nodes within this cone • The angle θ cannot be too small since RFID frequencies is usually 30 Mhz • Can show: # witness points is still bounded from above by O(n 3/ε 3 log (perimeter) )

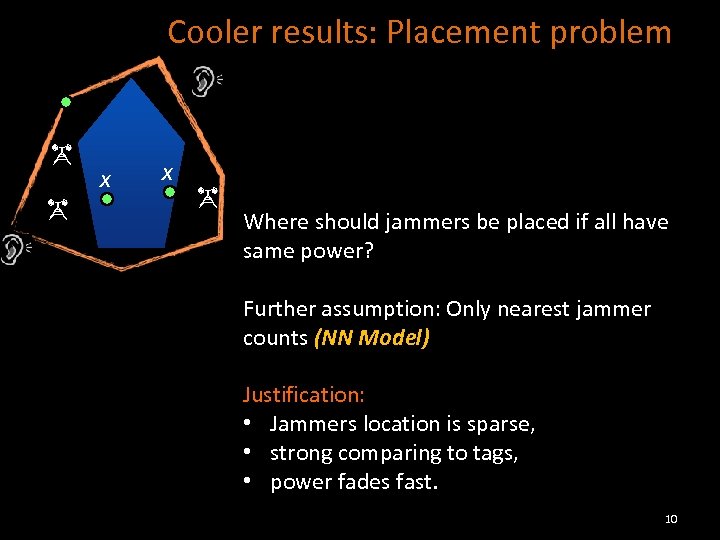Cooler results: Placement problem x x Where should jammers be placed if all have same power? Further assumption: Only nearest jammer counts (NN Model) Justification: • Jammers location is sparse, • strong comparing to tags, • power fades fast. 10

Placement problem (cont) First condition of successful jamming { Jamming Power inside Storage ≤ P 0 } => Jammer cannot lie within distance R 0 of storage Def: Forbidden Region: Union of all such Disks (minkovsky sum) 11

Placement problem (secondition) The condition D(pj) pj Let p be a point on fence. Boils down (under NN model) to . Def: the critical disk of p, D(p), is the smallest disk centered at p, and touching the storage. This disk must contain a jammer Continuous Hitting Set Problem: Place a minimum number of jammers so that all critical disks (of all fence points p) contain a jammer. 12

Greedy Approach D(p 1) D(p 2) 1. Start at any point p 1 on boundary and compute its critical disk. 2. Compute next point p 2 such that critical disks are tangent 3. Place first jammer at tangent point 4. Repeat Algorithm gives Opt+1 for convex case. 13

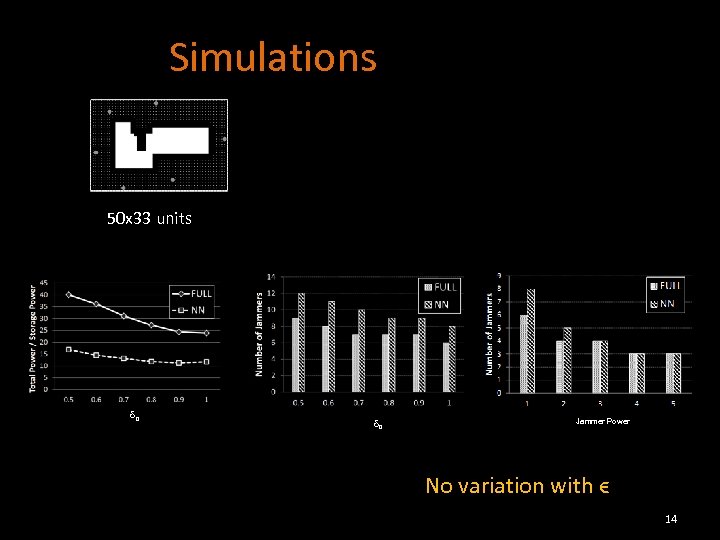Simulations 50 x 33 units δ 0 Jammer Power No variation with ϵ 14

Background • RFID Security – Blocker tag (Juels et al. , ACM CCS ‘ 03): Security tag on a bag containing the RFID tag interferes with readers outside. • Sensor network security – Most techniques focus on cryptography where the main problem is key management (Simplicio Jr. et al. , Computer Networks, ’ 10) • General Wireless security – Active Jamming • Commander et al. , Journal of Combinatorial Optimization, ’ 07 • Do not consider geometry of region – Information Theoretic Approaches • Lai and El Gamal, IEEE Trans. On Information Theory, ‘ 08; Negi and Goel, IEEE VTC, ’ 05; Tang et al. , IEEE Trans. On Information Theory, ’ 11; Vilela et al. , IEEE Trans. On Information Forensics and Security, ’ 11 15

Thank you 16