Optimization of Systems Governed by PDEs Algorithms and

Optimization of Systems Governed by PDEs: Algorithms and Applications in Computational Science and Engineering Omar Ghattas TOPS Sci. DAC + Carnegie Mellon University

The “simulation problem” (forward, state, direct)

The “optimization problem” (inverse, design, control)

Karush-Kuhn-Tucker first order optimality conditions

A peak at the basic algorithm Given est. of d, solve state eqn for u Given d & u, solve adjoint eqn for p Given u & p, solve opt eqn to update d Numerous issues related to globalization, inexactness, time dependent problems, continuation, preconditioning, Krylov solvers, multilevel algorithms See V. Akcelik, G. Biros, O. Ghattas, J. Hill, D. Keyes, and B. van Bloemen Waanders, “Parallel Algorithms for PDE-constrained optimization”, Frontiers of Parallel Scientific Computing, M. Heroux, P. Raghavan, and H. Simon, eds. , SIAM, 2006, to appear.

PDE-constrained optimization: Why now? • Maturing state of models, discretization, and solvers forward problems • Emergence of large-scale finite-dimensional nonlinear optimization algorithms • Rapid rise in high-end computing capability • Improvements in quality of observational data • Optimization is often what is of ultimate interest

PDE-constrained optimization: Challenges • All of the forward simulation components must be automated, online, and parallel • For large optimization variable dimensions (or for high precision), need gradient (and often Hessian) based algorithms • Efficient gradients require adjoint PDE solves • Specialized algorithms required for solution of the coupled optimality system • Optimization of terascale-class problems is a petascale-level challenge

Illustrations of PDE-based optimization • Optimal control: o Optimal boundary control of Navier-Stokes flows (*) • Inverse problems: o Earthquake inversion for earth properties (*) • Optimal design: o Shape optimization of linear accelerators * = PETSc-powered

Optimal boundary flow control minimize subject to: Joint work with George Biros, Penn [SIAM J Sci Comp 2005]

Strong form of 1 st order optimality system • Forward problem • Adjoint • Control

Flow around Boeing 707 Wing • 700, 000 states • 4, 000 controls • 128 procs (T 3 E) • ~5 hrs (LNKS-PR-TN) • Continuation

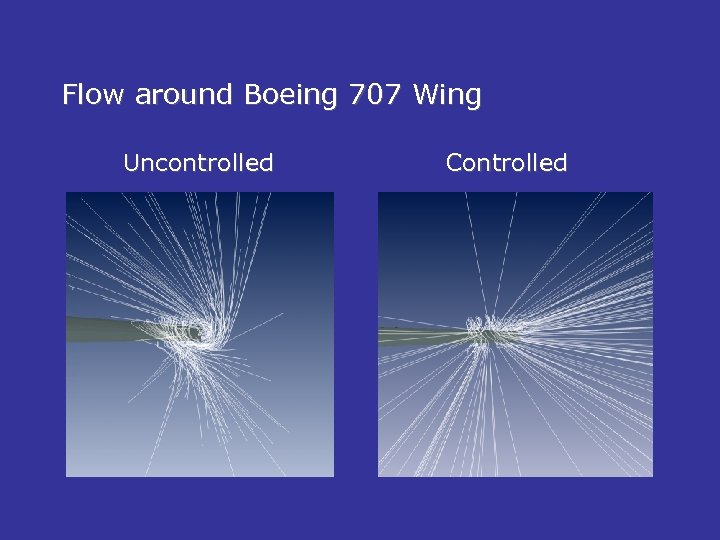
Flow around Boeing 707 Wing Uncontrolled Controlled

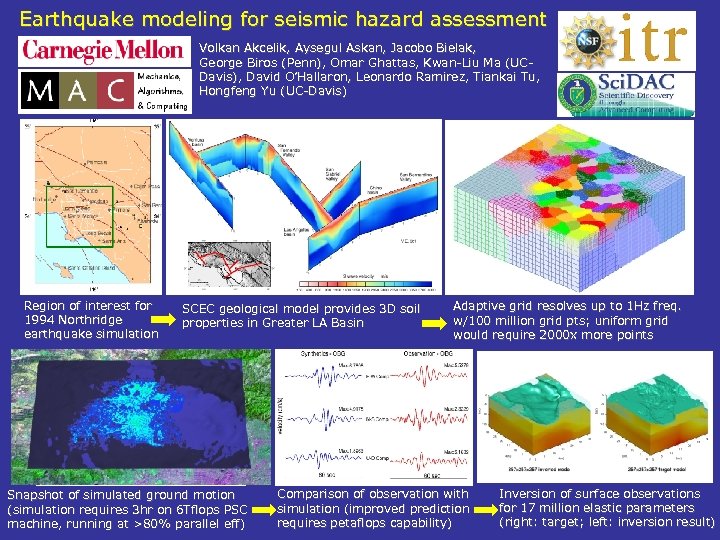
Earthquake modeling for seismic hazard assessment Volkan Akcelik, Aysegul Askan, Jacobo Bielak, George Biros (Penn), Omar Ghattas, Kwan-Liu Ma (UCDavis), David O’Hallaron, Leonardo Ramirez, Tiankai Tu, Hongfeng Yu (UC-Davis) Region of interest for 1994 Northridge earthquake simulation SCEC geological model provides 3 D soil properties in Greater LA Basin Snapshot of simulated ground motion (simulation requires 3 hr on 6 Tflops PSC machine, running at >80% parallel eff) Adaptive grid resolves up to 1 Hz freq. w/100 million grid pts; uniform grid would require 2000 x more points Comparison of observation with simulation (improved prediction requires petaflops capability) Inversion of surface observations for 17 million elastic parameters (right: target; left: inversion result)

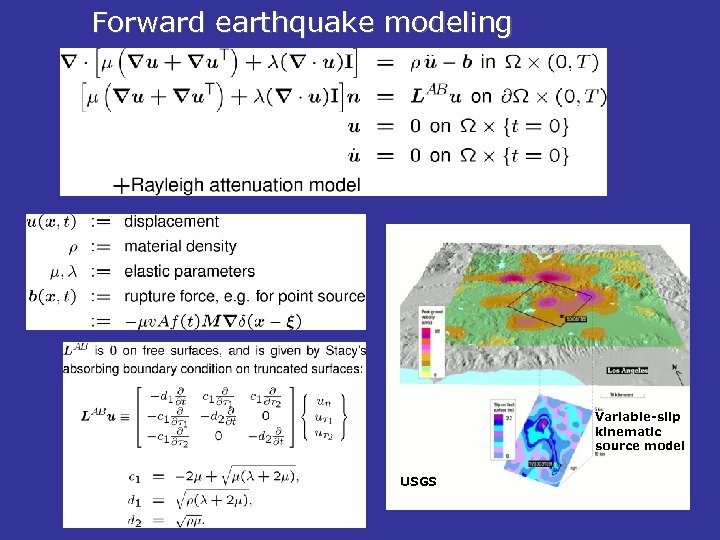
Forward earthquake modeling Variable-slip kinematic source model USGS

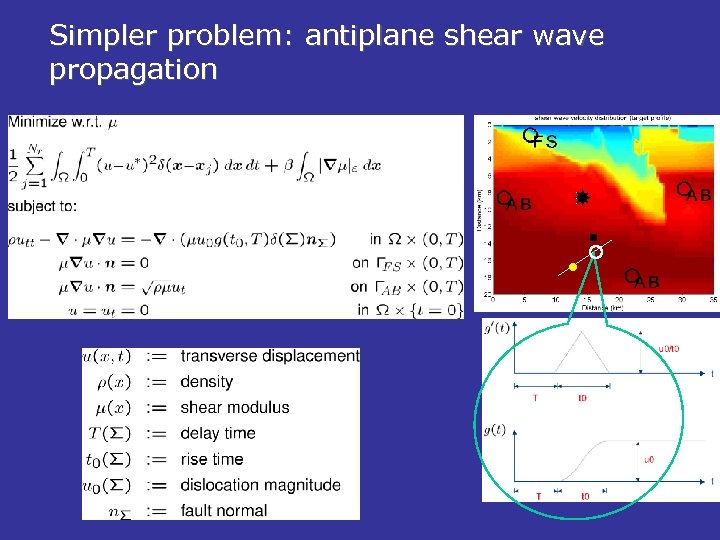
Simpler problem: antiplane shear wave propagation

Strong form of first order necessary conditions

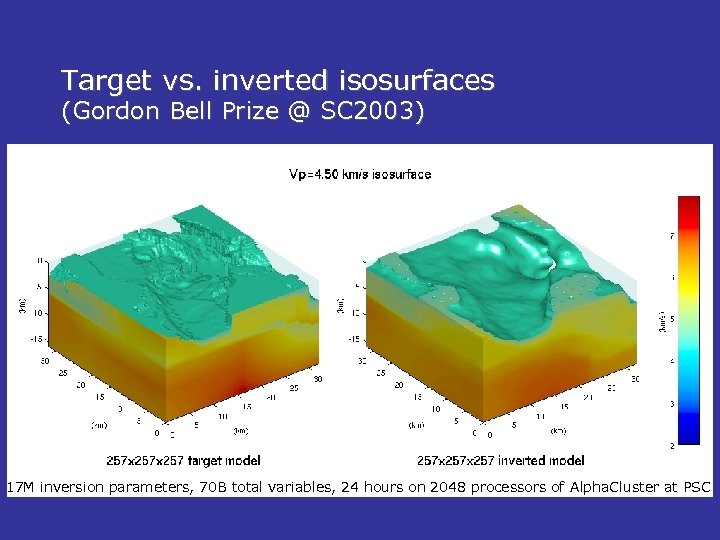
Target vs. inverted isosurfaces (Gordon Bell Prize @ SC 2003) 17 M inversion parameters, 70 B total variables, 24 hours on 2048 processors of Alpha. Cluster at PSC

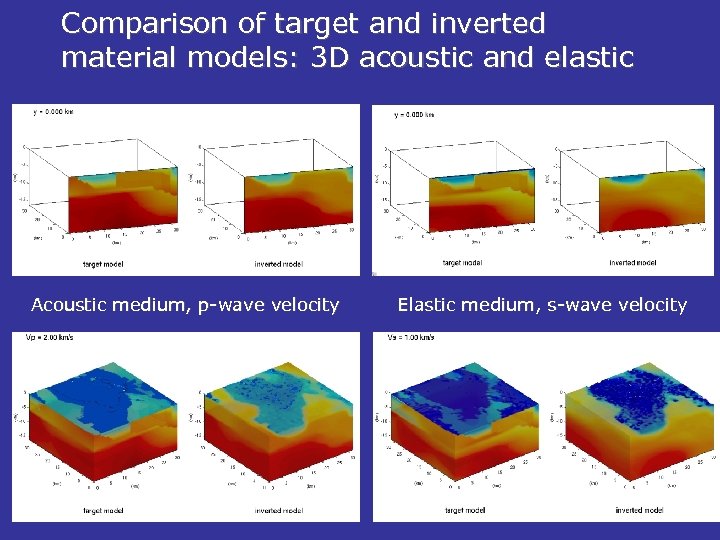
Comparison of target and inverted material models: 3 D acoustic and elastic Acoustic medium, p-wave velocity Elastic medium, s-wave velocity

Shape Optimization for Accelerator Structures Rich Lee Kwok Ko Volkan Akcelik Omar Ghattas George Biros David Keyes Esmond Ng Patrick Knupp Tim Tautges Lori Diachin Mark Shephard

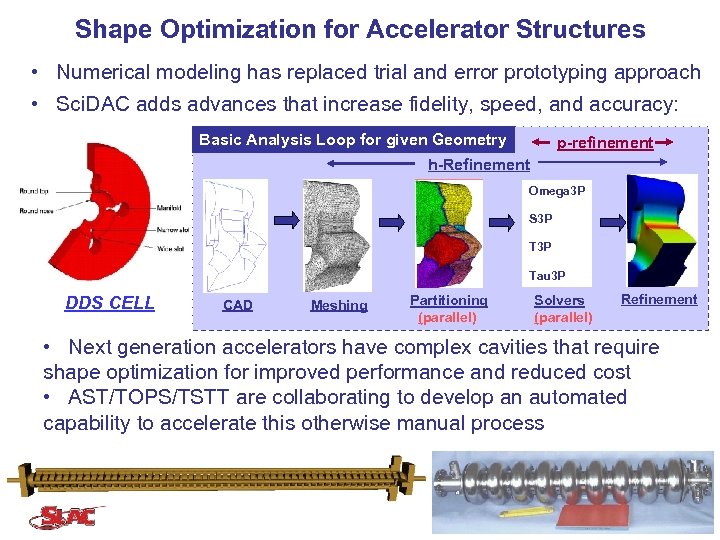
Shape Optimization for Accelerator Structures • Numerical modeling has replaced trial and error prototyping approach • Sci. DAC adds advances that increase fidelity, speed, and accuracy: Basic Analysis Loop for given Geometry p-refinement h-Refinement Omega 3 P S 3 P Tau 3 P DDS CELL CAD Meshing Partitioning (parallel) Solvers (parallel) Refinement • Next generation accelerators have complex cavities that require shape optimization for improved performance and reduced cost • AST/TOPS/TSTT are collaborating to develop an automated capability to accelerate this otherwise manual process

Difficulties in Automated Shape Optimization for Accelerator Structures • Gradient-based optimization essential to manage large design space, expensive state simulation (a Maxwell eigenvalue solve for frequencies of interest), and high accuracy requirements • Need to compute derivatives of design goals with respect to design parameters (CAD parameterization of geometry • Finite difference approximation of gradient inaccurate and intractable: would require tens of eigenvalue solves per design iteration! • Optimization of shape often requires derivatives of mesh motion and CAD parameterization • Remeshing new geometry necessary at each design iteration • All function and gradient computations, remeshing, and optimization steps must scale well to large numbers of state parameters and processors

Approach for Addressing Difficulties • Adopt adjoint sensitivity methods: only a handful of (linearized) eigenvalue solves needed at each design iteration (but need to develop capability to solve adjoint eigenvalue problem) • Compute gradient from infinite-dimensional form: avoids differentiation of meshing algorithm (but need to develop capability to evaluate surface integrals with higher-order derivatives of solution and geometry) • Build on TSTT parallel remeshing and CAD capabilities • Tailor TOPS parallel optimization algorithms to structure of accelerator design problem

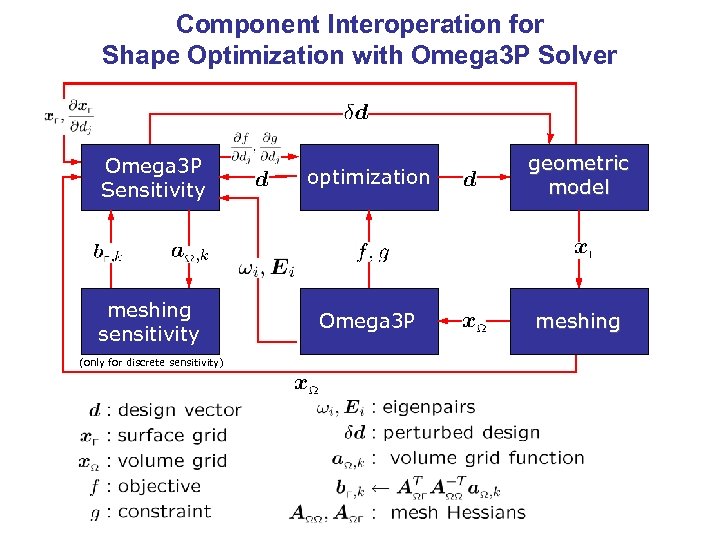
Component Interoperation for Shape Optimization with Omega 3 P Solver Omega 3 P Sensitivity optimization geometric model meshing sensitivity Omega 3 P meshing (only for discrete sensitivity)

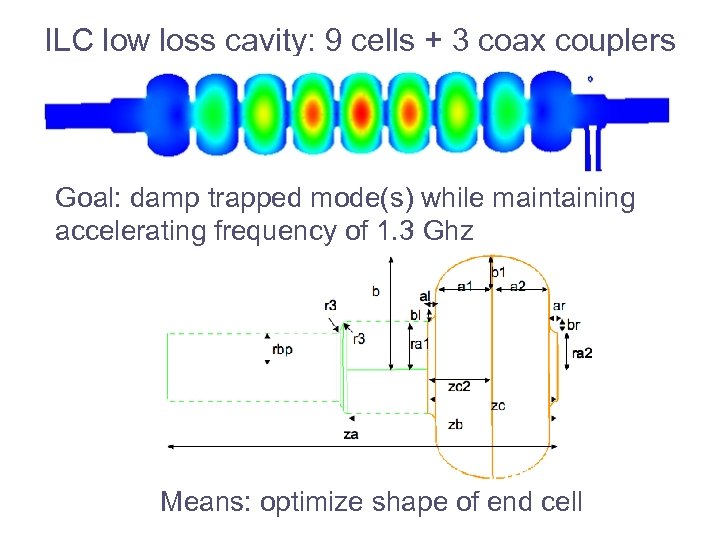
ILC low loss cavity: 9 cells + 3 coax couplers Goal: damp trapped mode(s) while maintaining accelerating frequency of 1. 3 Ghz Means: optimize shape of end cell

Shape optimization problem: Damp well-trapped dipole modes while maintaining the accelerating frequency

Optimality conditions (consider one controlled mode, penalize frequency)

Optimality conditions, continued

Comparison of Sensitivity for 1/Q 5 2 c 3 4 b 1 a c=0. 10 a=0. 08 b=0. 06 6

Minimizing 1/Q with Freq=2. 0 GHz c b a Electric BC on all surfaces

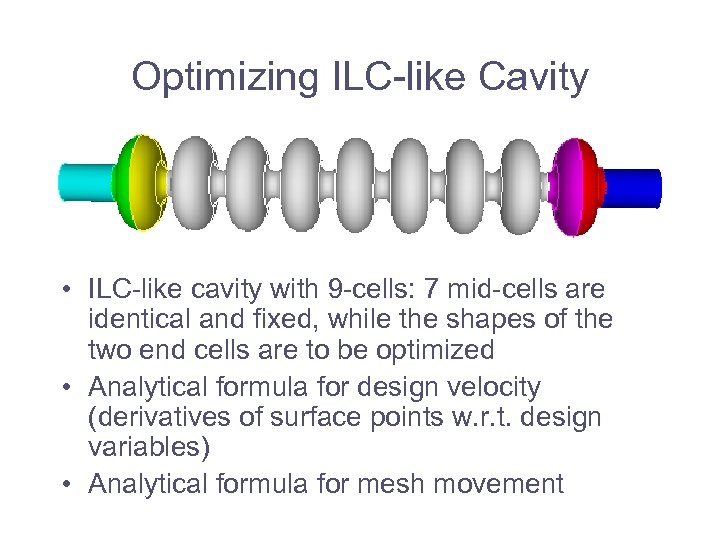
Optimizing ILC-like Cavity • ILC-like cavity with 9 -cells: 7 mid-cells are identical and fixed, while the shapes of the two end cells are to be optimized • Analytical formula for design velocity (derivatives of surface points w. r. t. design variables) • Analytical formula for mesh movement

End Cell Dimensions a 1 b 2 b 1 a 2 R L b • The cell is cylindrically symmetric and consists of 4 quarters of ellipse curves (ai, bi) • We choose R, a 1, b 1, and b as independent design variables • Others are either dependent (a 2, b 2, …) or fixed (L, a 4, b 4, …)

ILC-like shape optimization: first results • Maximize the stored energy of a dipole mode in the end cell while satisfying acc - * = 0 • Initial design variables: – R=41 mm, a 1=17. 590 mm, b 1=20 mm, b=103. 36 mm – Uendcell = 0. 31%, = -0. 04756 • After five optimization iterations, optimized solution is found: – R=40. 992 mm, a 1=17. 571 mm b 1=20. 008 mm, b=103. 455 mm – Uendcell = 0. 49%, = -3. 75 e-6

Final Remarks • Maturing state of forward solvers and emerging capabilities for PDE-constrained optimization invite what is often the ultimate goal: simulation-based optimization (design, control, inversion) • Optimization problems with 106 – 108 variables can be solved in as little as 5 -10 X the forward simulation time • Shape optimization brings additional challeges of the highest order: – requires CAD/mesh/solvers to be fast, automated, differentiable, scalable • Continuous adjoints provide design variable independence, require only surface mesh sensititivies • Parallel mesh movement capability essential • Huge effort: worse than writing solver code from scratch • But huge potential payoff for design of multi-billion dollar devices