Оптимизация технологических и процессов общественного питания 18 ч

Зарегистрируйтесь, чтобы просмотреть полный документ!

Оптимизация технологических и процессов общественного питания 18 ч. Лекций, 36 ч. практических работ, 126 ч. cамостоятельной работы, экзамен

Оптимизация – поиск оптимума § Оптимумом, или оптимальным вариантом называется вариант, который является наилучшим среди допустимых при наличии правила предпочтения одного другому. § Такое правило предпочтения называется критерием оптимальности. § Мера предпочтения – показатель качества (параметр оптимизации). Основные подходы к оптимизации технологических процессов: § Бессистемно-случайный § Интуитивно-логический § Научный (как правило, математический)

Литература 1. Разработка новых видов пищевых продуктов [Электронный ресурс] : метод. указания к выполнению практ. работы "Изучение методов оптимизации технологических режимов основных технологических операций на этапе изготовления пищевой продукции" для студентов направлений подгот. 100800. 62 "Товароведение", 260200. 62 "Продукты питания животного происхождения" и специальности 080401. 65 "Товароведение и экспертиза товаров в сфере таможенной деятельности" / Федер. агентство по рыболовству, Мурман. гос. техн. ун-т, Каф. технологий пищевых пр-в ; сост. Ю. В. Шокина. - Мурманск : Изд-во МГТУ, 2014 2. Глазунов, Ю. Т. Моделирование процессов пищевых производств : учеб. пособие для вузов / Ю. Т. Глазунов, А. М. Ершов, М. А. Ершов ; Центр. учеб. -метод. каб. Гос. ком. РФ по рыболовству. - Москва : Колос, 2008. - 358 с. : ил. - (Учебник). - Библиогр. : с. 341 -343. - ISBN 978 -5 -10 -0040187 : 293 -00. 3. Алексеев, Г. В. Математические методы в пищевой инженерии: Учебное пособие / Г. В. Алексеев, Б. А. Вороненко, Н. И. Лукин. – СПб. : Издательство «Лань» , 2012. – 176 с. : ил. 4. Стефановский Н. В. и др. Процессы и аппараты рыбообрабатывающих производств. - М. ; Легкая и пищевая промышленность, 1984 -236 стр. 5. Адлер, Ю. П. Планирование эксперимента при поиске оптимальных условий / Ю. П. Адлер [и др. ]. Изд. 2 -е, перераб. и доп. - М. : Наука, 1976. – 280 с.

Классификация видов оптимизации § § По количеству критериев (однокритериальная и многокритериальная) По наличию дополнительных условий (безусловная и условная) По используемым математическим и/или вычислительным методам (линейное, нелинейное программирование; метод крутого восхождения; методы нечёткой логики и т. д. ) По способу получения целевой(ых) функции(ий) (методы планирования экспериментов, методы регрессионного анализа, методы корреляционного анализа; метод искусственных нейронных сетей; методы на основе анализа дифференциальных уравнений; методы на основе теории подобия и др. )

Этапы оптимизации технологического процесса 1. Постановка задачи 1. 1. Определение параметров, подлежащих оптимизации и установление ограничений 1. 2. Поиск влияющих факторов 1. 3. Выбор критерия оптимальности 2. Получение целевой функции (математической модели). 3. Решение задачи оптимизации математическими и/или вычислительными методами 4. Интерпретация результатов и распространение их на реальный объект 5. Оценка оптимальности полученных результатов.

Критерий оптимальности § § § Правильный выбор критерия оптимальности – это залог успеха всего процесса оптимизации. Высокая субъективность выбора: ответ на вопрос «Что лучше» Распространённый пример: соотношение «цена/качество» Дополнительные условия при оптимизации (безопасность продукции и производства, минимальный уровень качества или минимальная рентабельность и т. д. ) Показатели качества продукции: объективные и субъективные. Выбор показателей (параметров) для критерия оптимальности

Требования к параметрам оптимизации § § Простота определения Высокая воспроизводимость Очевидное направление оптимизации Взаимосвязь с общей оценкой привлекательности продукции (услуг)

Примеры параметров оптимизации § § § Общая рентабельность предприятия; окупаемость капитальных вложений Себестоимость на единицу продукции или её часть Показатели пищевой и биологической ценности (энергетическая ценность, биологическая ценность белка, КЭБ, процент удовлетворения суточной потребности и т. д. ) Уровень качества по органолептичекой оценке Эстетические и эргономические показатели Показатели, коррелирующие с вышеперечисленными

Примеры дополнительных условий оптимизации § § § § Показатели безопасности (не выше допустимых норм с учётом запаса) Минимальная рентабельность предприятия/максимум капитальных вложений Минимально-приемлемое качество по каждому органолептическому показателю Предельные значения показателей назначения (массовая доля соли, сахара, влаги и т. д. ) Минимальная или максимальная энергетическая ценность Максимальные режимные параметры технологического процесса Естественные пределы изменения параметров

Подходы к решению многопараметрических задач § Оптимизация с несколькими целевыми функциями (многокритериальная оптимизация) § Замена некоторых параметров оптимизации дополнительными условиями § Формирование единой целевой функции как линейной или нелинейной комбинации от всех параметров оптимизации § Использование методов нечёткой логики для формирования условий оптимальности.

Обобщённые параметры оптимизации § Уровень качества по органолептической оценке: § Комплексный безразмерный показатель качества: § Аналогично при степенном подходе

Нормирование параметров 1. Из в 2. Из в 3. Обратное преобразование: в 4. Из в 5. Из в

Распространённые ошибки при выборе обобщённого параметра оптимизации 1. Отдельные параметры оптимизации не прошли нормирование и могут меняться совсем в другом диапазоне, тогда как коэффициенты значимости это не учитывают. 2. Один из параметров оптимизации имеет явный оптимум, который не был учтён, тогда как остальные должны только возрастать или убывать. 3. Параметры, которые должны возрастать, складываются или умножаются на параметры, которые должны убывать без учёта этого дополнительным коэффициентом. 4. Два или более параметра связаны друг с другом (неоправданно увеличивается значимость) 5. Ошибки выбора коэффициентов значимости 5. 1. Коэффициенты значимости не выбираются, а условно принимаются равными 5. 2. Сумма коэффициентов значимости маловажных параметров оказывается неоправданно завышенной 5. 3. Ошибки в нормировке максимального значения обобщённого параметра оптимизации с помощью коэффициентов значимости 6. Обобщённым параметром оптимизации пытаются учесть и неприемлемый результат по какому-то одному показателю (нейтрализуется другими)

Факторы 1. Варьируемые 2. Фиксируемые 3. Неуправляемые 3. 1. Управляемые пассивно 3. 2. Совершенно неуправляемые 4. Не учитываемые 5. Не влияющие (маловлияющие)

Интервал варьирования факторов § § § Естественные границы варьирования Нормирование уровней варьирования (-1; 0; +1) Возможный выход за пределы варьирования.

Методы получения целевой функции § § § § Анализ математических моделей Использование теории подобия Планирование эксперимента Интерполяционные модели Регрессионный и корреляционный анализ Искусственные нейронные сети Системы нечёткой логики

Моделирование технологических процессов § Натурное (эксперименты на реальном объекте) § Физическое (на основе теории подобия) § Аналоговое (аналогичное) моделирование (используя процессы другой природы) § Универсальное моделирование (имитационные модели, отражающие взаимосвязи реального объекта) § Математическое моделирование

Основы теории подобия § § § Подобие – это полная математическая аналогия при наличии пропорциональности между сходственными переменными, сохраняющаяся при всех возможных значениях переменных Два объекта являются подобными, если соотношение как геометрических, так и физических величин между объектами одинаково. Критерии подобия: симплексы (отношение одноимённых величин) и комплексы (комбинация разноимённых величин) Абсолютное подобие – у подобных процессов равны все критерии. На практике встречается крайне редко (имеются несовместимые критерии даже при геометрическом подобии) Практическое подобие предполагает подобие только определённых, рассматриваемых свойств объекта. Может быть полным – подобие наблюдается в пространстве и во времени, неполным (или в пространстве, или во времени), приближённым (только в пределах допущений)

Теоремы подобия § Первая теорема (необходимое условие подобия) - для подобных явлений существуют равные критерии подобия § Вторая теорема (π-теорема) - число критериев подобия равно количеству всех размерных факторов за вычетом числа основных единиц измерения, входящих в размерность факторов § Третья теорема – необходимыми и достаточными условиями подобия являются пропорциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия Получение математических моделей на основеуравнений (опускаются знаки дифференцирования и теории подобия 1. Упрощение дифференциальных выделяются критерии подобия) 2. Метод анализа размерностей

Основы теории планирования эксперимента § Основная задача планирования эксперимента – минимизация количества опытов для получения максимальной информации об объекте. § Для анализа линейных и близких к линейным зависимостей достаточно двух уровней варьирования факторов – эксперимент вида 2 n (n – число факторов) § Уровни варьирования факторов нормируются до -1 … +1 (иногда обозначают «–» и «+» ). § Однофакторное планирование – 21: -1 +1.

Полный факторный эксперимент 2 n X 1 X 2 +1 +1 -1 -1 -1 Y Х 1 Х 2 Х 3 +1 -1 +1 +1 -1 -1 Y

Дробный факторный эксперимент § § § Рост числа влияющих факторов приводит к экспоненциальному росту числа опытов ПФЭ позволяет получить (без учёта оценки погрешности) линейную модель с эффектами взаимодействий. Например, по плану 22 можно получить уравнение (так как имеется 4 уравнения, то можно определить 4 неизвестных коэффициента, хотя для регрессии требуется хотя бы одна степень свободы) Если есть основания полагать, что эффекты взаимодействия отсутствуют, т. е. факторы влияют на параметр оптимизации линейно и независимо, то один из опытов в плане «лишний» , и его можно опустить. Для эксперимента 22 это редко бывает актуальным, т. к. 4 опыта вполне можно провести, а «экономия» составляет всего лишь 1 опыт. Для плана 23 уравнение будет иметь вид (т. е. на 8 опытов приходится 8 коэффициентов). Если же опустить все эффекты взаимодействия, то получится всего лишь 4 опыта. Их называют «полурепликой» 23 -1

Полуреплика 23 -1 Х 2 Х 3 +1 -1 -1 +1 Y +1 +1 -1 -1 Фактически, здесь X 3 выбирается как эффект взаимодействия для ПФЭ 22: Х 1 Х 2.

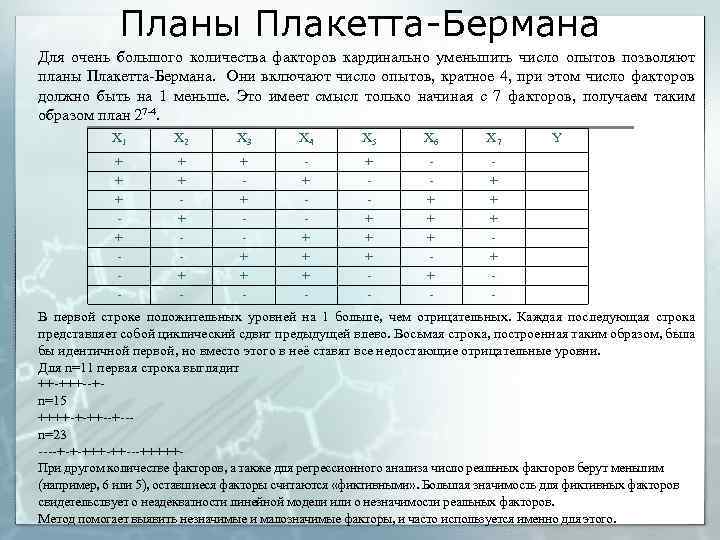
Планы Плакетта-Бермана Для очень большого количества факторов кардинально уменьшить число опытов позволяют планы Плакетта-Бермана. Они включают число опытов, кратное 4, при этом число факторов должно быть на 1 меньше. Это имеет смысл только начиная с 7 факторов, получаем таким образом план 27 -4. Х 1 Х 2 Х 3 Х 4 Х 5 Х 6 Х 7 + + + + - + + + + - Y + + - В первой строке положительных уровней на 1 больше, чем отрицательных. Каждая последующая строка представляет собой циклический сдвиг предыдущей влево. Восьмая строка, построенная таким образом, была бы идентичной первой, но вместо этого в неё ставят все недостающие отрицательные уровни. Для n=11 первая строка выглядит ++-+++--+n=15 ++++-+-++--+--n=23 ----+-+-++---+++++При другом количестве факторов, а также для регрессионного анализа число реальных факторов берут меньшим (например, 6 или 5), оставшиеся факторы считаются «фиктивными» . Большая значимость для фиктивных факторов свидетельствует о неадекватности линейной модели или о незначимости реальных факторов. Метод помогает выявить незначимые и малозначимые факторы, и часто используется именно для этого.

Композиционные планы § § § Дробные и полные планы эксперимента с двумя уровнями варьирования позволяют работать с линейными зависимостями, при учёте эффектов взаимодействия допускается некоторая нелинейность. Вблизи экстремума даже ПФЭ 2 n не позволяет изучить поверхность отклика (график целевой функции) и, как следствие, не подходит для решения задач оптимизации. В случае, если имеются основания предполагать наличие экстремума в пределах варьирования факторов, следует применять композиционные планы, включающие ПФЭ и «звёздные» точки – точки, находящиеся на осях плана и отстоящих от него на определённую величину – плечо (γ). Кроме того, в состав многих композиционных планов вводят одну или несколько точек в центре плана. Если факторы симметричны относительно центра плана, то такой план называют центральным композиционным планом (ЦКП). К ЦКП часто предъявляют требования ортогональности (сумма произведений элементов матрицы планирования равна нулю). В этом случае плечо звёздных точек можно принять 1, т. е. звёздные точки будут в середине боковых сторон (граней, гиперграней) квадрата (куба, гиперкуба). Для большей адекватности модели чаще всего пользуются рототабельным ЦКП, в котором звёздные точки можно получить поворотом ПФЭ относительно центра на определённый угол.

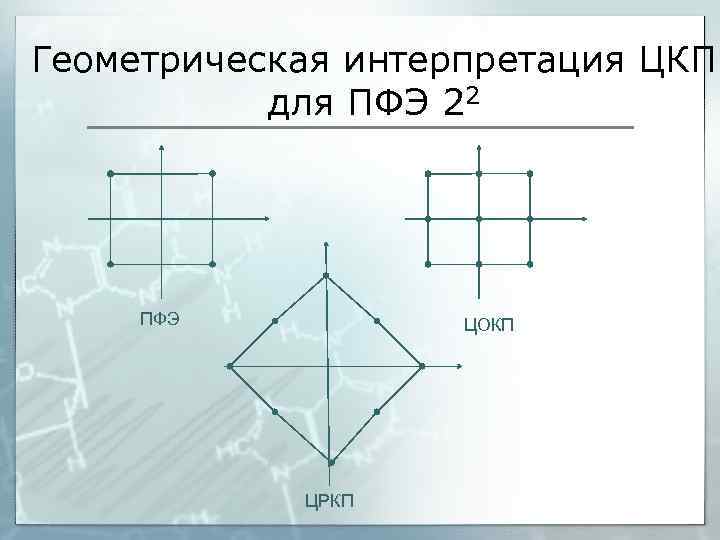
Геометрическая интерпретация ЦКП для ПФЭ 22 ПФЭ ЦОКП ЦРКП

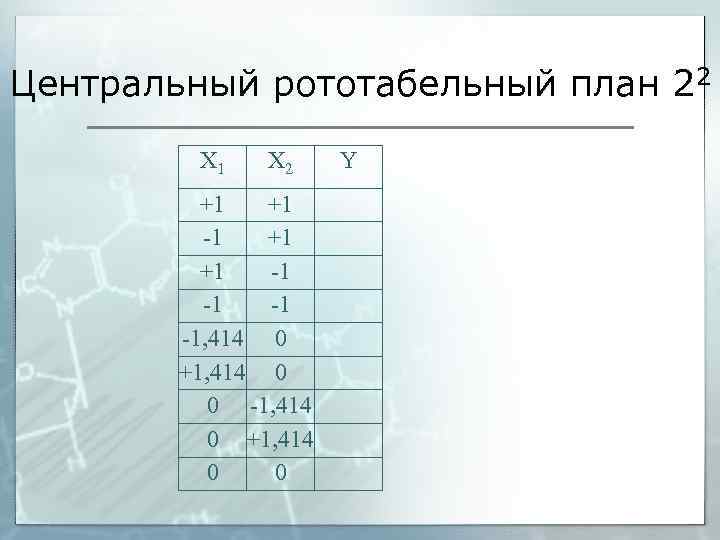
Центральный рототабельный план 22 Х 1 Х 2 +1 +1 -1 -1, 414 0 +1, 414 0 0 Y

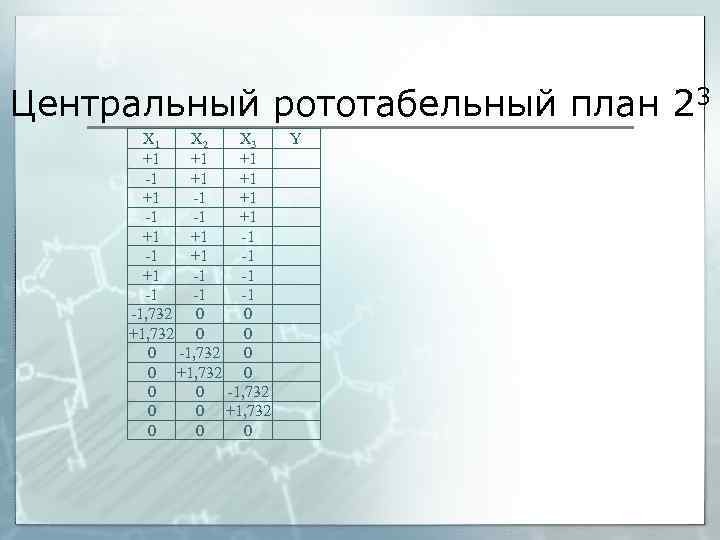
Центральный рототабельный план 23 Х 1 Х 2 Х 3 +1 +1 +1 -1 -1 +1 +1 +1 -1 -1 -1, 732 0 0 +1, 732 0 0 0 Y

Особенности практического использования теории планирования эксперимента § Необходимость учёта ошибки опытов – повторные эксперименты (особенно в центре плана) § Систематическая ошибка, связанная с последовательностью опытов – переводится в случайную рандомизацией. § Необходимость получить несколько степеней свободы для регрессионного анализа § Правильное нормирование факторов (с учётом запаса на «звёздные точки» ) § Возможность многократного планирования с последующим движением методом «крутого восхождения»

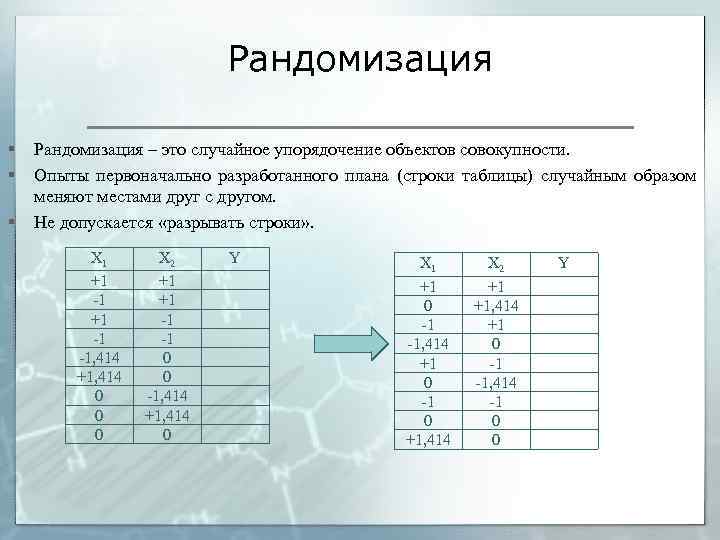
Рандомизация § § § Рандомизация – это случайное упорядочение объектов совокупности. Опыты первоначально разработанного плана (строки таблицы) случайным образом меняют местами друг с другом. Не допускается «разрывать строки» . Х 1 +1 -1 -1, 414 +1, 414 0 0 0 Х 2 +1 +1 -1 -1 0 0 -1, 414 +1, 414 0 Y Х 1 +1 0 -1 -1, 414 +1 0 -1 0 +1, 414 Х 2 +1 +1, 414 +1 0 -1 -1, 414 -1 0 0 Y

Предварительная обработка экспериментальных данных 1. Обработка результатов повторяющихся опытов 2. Обработка «временных рядов» и последовательных экспериментов § 2. 1. Сглаживание § 2. 2. Интерполяция 3. Работа с разнородными выборками 3. 1. Дисперсионный анализ 3. 2. Корреляционный анализ

Сглаживание экспериментальных данных § § § Графический интуитивный метод Регрессионные методы (МНК) Упрощённые методы сглаживания (кроме первой и последней точек)

Интерполяция и интерполяционные модели § § Интерполяция – способ получения промежуточных данных по имеющимся точкам В большинстве случаев методы интерполяции не проходят статистического обоснования. Методы интерполяции § Метод ближайшего соседа § Линейная интерполяция § Полиномиальная интерполяция (формулы Ньютона, Лагранжа, сплайн-интерполяция и т. д. ) Достоинства полиномиальной интерполяции: § Позволяет получить гладкую функцию § Не требует сложных статистических обоснований Недостатки полиномиальной интерполяции: § Есть риск получить экстремум при отсутствии предпосылок к нему § Неэффективна при значительной случайной ошибке опытов

Дисперсионный анализ § § § Позволяет оценить, влияет ли фактор на параметр оптимизации Использует F-распределение (критерий Фишера) Многофакторный дисперсионный анализ позволяет оценить эффекты взаимодействия Термины, определения, обозначения xi, j – единичное измерение в группе (выборке) i, имеющее порядковый номер j M – математическое ожидание генеральной совокупности, равное среднему арифметическому. Мi – математическое ожидание i-й выборки (равное среднему арифметическому выборки). SS – сумма квадратов отклонений. SSi=(xi, j –Mi) для i-й выборки (внутригрупповая сумма квадратов отклонений, SSWG) Выделяют общую сумму квадратов отклонений, SSt, внутригрупповую SSWG и межгрупповую SSBG (связанную с различием математических ожиданий) D – дисперсия (иногда обозначается MS). Равна сумме квадратов отклонений, делённому на число степеней свободы. F – критерий Фишера. Равен отношению двух дисперсий.

Последовательность однофакторного дисперсионного анализа § Выбирается несколько выборок данных (не менее 2), различающихся значением фактора § В каждой выборке определяют сумму квадратов SSWG § Нулевая гипотеза – все мат. ожидания равны (М=М 1=М 2=…) § Проверка гипотезы: где J – число групп (выборок) где N – объём полной выборки (общее число опытов) § Рассчитанный критерий Фишера сравнивают с табличным, если он больше, то нулевую гипотезу отвергают с доверительной вероятностью. В противном случае нельзя исключить, что фактор не влияет на параметр оптимизации, такие факторы называют незначимыми или малозначимыми. Для более точного результата следует повторить анализ с большими объемами выборок и количеством групп.

Многофакторный дисперсионный анализ §

Факторный анализ § Позволяет сократить количество факторов (или параметров оптимизации) за счёт удаления взаимосвязанных Методы факторного анализа § Метод главных компонент § Корреляционный анализ § Метод максимального правдоподобия

Корреляционный анализ § § Корреляция – статистическая зависимость двух или более случайных (или условно случайных) величин. При наличии двух случайных величин взаимную зависимость проверяют через коэффициент корреляции где sx и sy – среднеквадратические отклонения x и y как случайных величин sxy – ковариация между двумя величинами где Mx , My и Mxy – математические ожидания x, y и их произведения n – число точке (пар x и y) Таким образом

Особенности коэффициента корреляции (на графиках) r 1 r <1 r ≈0 r -1 r ≈0

Ограничения коэффициента корреляции § § Все величины должны быть распределены нормально Для значимого результата необходимо большое число измерений Не позволяет выявить существенно нелинейную зависимость Корреляционный анализ не позволяет утверждать о причинноследственной зависимости: выбор x и y в рамках анализа произволен и «лежит на совести» экспериментатора; не исключено наличие третьего (не учтённого) параметра, влияющего на оба. § Коэффициент корреляции не следует использовать при взаимном влиянии трёх и более факторов

Множественная корреляция § § Оценивается теснота связи одной величины y и нескольких влияющих на неё x 1, x 2, x 3 и т. д. Коэффициент множественной корреляции R может быть получен по формуле где Dост – остаточная дисперсия по линейной модели (yp=a+b x 1+с x 2+…), равная Dy – дисперсия зависимой переменной y Квадрат коэффициента множественной корреляции называют коэффициентом детерминации Коэффициент частной корреляции, характеризующий влияние на y только xi :

Анализ математических моделей § Решение дифференциального уравнения для частной задачи - аналитическими методами - численными методами: обыкновенные ДУ – метод Эйлера, Рунге-Кутты; ДУ в частных производных – метод сеток § Выражение параметра оптимизации из модели § Использование интерполяционных моделей (при практическом отсутствии или предварительном исключении случайной ошибки) § Регрессионный анализ

Регрессионный анализ § Регрессионный анализ – это статистический метод исследования влияния одной или нескольких независимых переменных на зависимую. § Регрессионный анализ предполагает анализ предварительно заданной модели (уравнения регрессии), включая подбор коэффициентов, оценку адекватности модели и значимости коэффициентов регрессии. Регрессию можно классифицировать: § По числу факторов – на парную (только один фактор) и множественную § По характеру модели – на линейную и нелинейную. В общем случае задача регрессии имеет вид: Необходимо определить коэффициенты регрессии ai при наличии k наборов значений y и xj. Для корректного решения задачи необходимо, чтобы k>m, причём число степеней свободы будет f=k-m. Часто исходные данные записывают в матричной форме: вектор Y; матрица Х

Определение коэффициентов регрессии § § Наиболее распространённый метод – метод наименьших квадратов (МНК) Задача: где ypl – расчётное значение y для набора данных № l. Для линейных и близких к линейным (относительно коэффициентов регрессии ai) моделей существует только один экстремум выражения (1), он же будет минимумом. Для его нахождения надо решить систему уравнений, получаемых дифференцированием выражения (1) по каждому коэффициенту регрессии и приравниваемых к 0. В итоге получается m уравнений с m неизвестными, которые легко решить. В случае существенной нелинейности относительно коэффициентов регрессии необходима дополнительная проверка полученного решения на минимальность. Возможно также применение численных методов нахождения экстремума для существенно нелинейных моделей регрессии.

Подходы к сведению моделей к линейным § § § Математический аппарат для парной и множественной линейной регрессии хорошо отработан, имеется большое количество ПО (в т. ч. и СПО). Собственно линейная регрессия, как правило, не позволяет впоследствии решить задачу оптимизации. Полиномиальную регрессию легко свести к линейной: x 1 § x 2 x 3=x 1 x 2 x 4=x 12 x 5=x 22 y yp Таким образом, получают квадратичную модель § § Подобный метод можно использовать для простых нелинейных моделей: экспоненциальных, логарифмических и т. д. В настоящее время существует мощное ПО, решающее задачи нелинейной регрессии без сведения их к линейным

Оценка адекватности модели § § Подбор наилучших значений коэффициентов регрессии не гарантирует наилучший выбор модели – он лишь позволяет максимально возможно «подогнать» модель под исходные данные. Задача проверки адекватности модели – это задача опровержения «нуль-гипотезы» : «Модель описывает изменение y от xi не лучше, чем случайная ошибка» Для проверки гипотезы используют F-статистику (критерий Фишера) с двумя выборками: y как случайная величина и разность y-yp. Дисперсии этих величин соответственно называют дисперсией воспроизводимости S 2 y и дисперсией адекватности (остаточной дисперсией) S 2 ост. Первую считают при числе степеней свободы k-1 (k – число измерений), вторую – при k-m. Соотношение этих дисперсий даёт критерий Фишера, равный таким образом Полученный критерий Фишера сравнивают с табличным или оценивают по нему вероятность неадекватности модели. Большее значение F свидетельствует о большей адекватности уравнения регрессии.

Значимость коэффициентов регрессии § Адекватность уравнения регрессии характеризует его целиком, но отдельные факторы или эффекты могут влиять на параметр оптимизации незначительно. Проверка значимого отличия коэффициентов регрессии от 0 (реже от 1) §

Методы безусловной оптимизации Классификация : По требованиям к гладкости функции § Нулевого порядка; прямые методы (требуют только значения функции в отдельных точках) § Первого порядка (требуют наличие и непрерывность первых производных) § Второго порядка (требуют наличие и непрерывность вторых производных) По способу решения задачи § Аналитические § Численные § Графические

Методы с использованием производных (однофакторная задача) Необходимым условием экстремума является равенство нулю, разрыв или неопределённость первой производной (точка, подозрительная на экстремум). Достаточные условия экстремума (любое): § Смена знака первой производной в точке экстремума (с «-» на «+» – минимум, с «+» на «-» - максимум) § Ненулевое определённое значение второй производной в точке (отрицательное – минимум, положительное – максимум). Точки экстремума, найденного по производным, могут не быть минимальным или максимальным значением (оптимумом) на всём промежутке. Чтобы доказать, что в этой точке наблюдается оптимум, необходимо одно из следующих действий: § Проверка значений на краях интервала. Если при этом проверить точки, в которых производная равна 0 или не существует, то проверка достаточных условий не требуется. § Анализ функциональной зависимости. Простые (например, параболические) зависимости имеют один экстремум в той точке, где производная равна 0. § Анализ графика функции. Если на нём явно виден один экстремум, он совпадает с подозрительной точкой и явно выше (ниже при минимизации) значений вокруг него вплоть до границ интервала, дальнейших доказательств не требуется.

Методы с использованием производных (многофакторная задача) При наличии 2 и более факторов необходимым условием экстремума является равенство 0 всех первых частных производных в одной точке. При этом в этой точке может наблюдаться: § экстремум § «седло» (рис. 1). Экстремума в этой точке нет. § перегиб Проверка на наличие экстремума может проводиться с помощью вторых производных. Например, условием экстремума функции Рис. 1. Седловая f(x, y) является условие точка «Saddle point» . Под лицензией Общественное достояние https: //commons. wikimedia. org/wiki/File: Saddle_ point. png#/media/File: Saddle_point. png Максимум наблюдается, если вторая производная по x отрицательная, а минимум – если положительна. При Δ<0 экстремума нет, а при Δ=0 экстремум может быть, а может и не быть.

Многофакторная задача – практическое использование Поскольку при наличии нескольких факторов наибольшее/наименшее значение может быть как внутри границ, так и в любой точке границы функции, то, помимо точек, подозрительных на экстремум, необходимо рассмотреть все пограничные «срезы» . Например, для двухфакторной задачи f(x, y) в пределах x∈[x 1, x 2]; y∈[y 1, y 2] необходимо 1) найти точки, подозрительные на экстремум (первые производные функции по x и y обращаются в 0) 2) найти и проверить экстремумы (точки, подозрительные на экстремум) на следующих срезах, приравняв производные к 0: Таким образом, задача дополнилась 4 -мя задачами меньшей размерности. 3) Определить значения функции в углах диапазона: Максимальное (минимальное) значение в рассматриваемом диапазоне выбирают изо всех «подозрительных» точек. Если оно оказалось на краю диапазона (во всех случаях, кроме первого), то надо рассмотреть задачу расширения диапазона варьирования или доказать, что это невозможно (нецелесообразно).

Поисковый метод оптимизации. Методы нулевого порядка Задача поискового метода – определить оптимум без аналитического выражения или если оно имеет сложный характер. Методы нулевого порядка не предполагают нахождения производных функции. § Метод случайного поиска. Выбирается случайная точка X 0=(x 1, 0, x 2, 0, x 3, 0…) и шаг h. Шаг откладывают от начальной точки в случайном направлении. Если значение функции в этой точке лучше (больше для максимума, меньше для минимума) предыдущего, то направление выбрано верно, и полученную точку считают X 1, после чего продолжают поиск следующей точки (в большинстве случаев – в том же направлении, которое меняют на случайное при нарушении условия). Если оно хуже, то полученную точку отбрасывают, а направление случайно меняют. В модификациях метода также предусмотрено уменьшение шага при большом количестве неудачных шагов и увеличение при удачных. Недостаток – очень сложно установить оптимальность полученной точки. § Метод покоординатного спуска. Оптимизация каждый раз идёт только по одному фактору. Одну из координат меняют при заданных (иногда случайных) значениях координат. При улучшении функции продолжают движение в эту сторону, при ухудшении – направление меняют на противоположное, (в ряде случаев уменьшая шаг). Далее координату меняют. Процесс проводят до тех пор, пока не прекратится любое движение.

Симплекс-метод § § Основан на оптимизации только в точках симплекса – правильного многоугольника/многогранника/гипермногогранника в факторном пространстве с n+1 вершинами (n – число факторов). Для двухфакторного эксперимента используют правильные треугольники, для трёхфакторного – тетраэдры. На первой итерации выбирают определённым (часто – случайным) образом n+1 точек, в них проверяют условие оптимизации. Из них выбирают наихудшую точку, её отбрасывают и отражают симметрично относительно остальных. На каждой последующей итерации таким же образом заменяют наихудшую точку. Метод используют преимущественно в линейном программировании, но можно использовать и в случае безусловной оптимизации.

Градиентные методы (первого порядка) § Движение происходит по градиенту (для максимума) или против (для минимума). Градиент находят численным дифференцированием – для малого h функции f(x 1, x 2, …) Полученный вектор в ряде случаев нормализуют (делят на его модуль) и всегда умножают на шаг. Возможные модификации метода: § С постоянным шагом – шаг не изменяют, в итоге точка оптимума будет найдена с меньшей точностью. § С дроблением шага – шаг по мере приближения к оптимуму определённым образом уменьшают. § Метод наискорейшего спуска – шаг выбирается в направлении градиента методом одномерной оптимизации. § Метод оврагов – вблизи «оврагов» по градиентам делают два шага, а третий – по вектору, соединяющему две последние точки.

Метод второго порядка – метод Ньютона § Метод Ньютона (метод касательных) – позволяет решить уравнение с использованием первой производной; для задачи оптимизации (поиска точек равенства нулю производной) используют вторую производную.

Условная оптимизация § Представляет собой сочетание целевой функции и ряда условий: § § Линейное программирование – функции f, g, q… носят линейный характер относительно всех факторов. Чаще всего решается симплексметодом. Методы решения – симплекс-метод, метод эллипсоидов. Нелинейное программирование – целевая функция f носит нелинейный характер.

Системы нечёткой логики § § Нечёткая логика – это обобщение задач аристотелевой логики для характеристик, имеющих приблизительную качественную оценку. Задачи нечёткой логики и нечётких множеств могут ставиться в тех случаях, когда вопрос истинности или ложности некоторого заключения носит неабсолютный характер, в т. ч. словесное, а не числовое описание. Не следует путать задачи нечёткой логики, когда характеристика известна, но носит приблизительный, описательный характер, и задачи теории вероятности, когда точной информации о некотором событии нет, но имеется вероятность его возникновения. Следует обратить внимание на теорию нечётких множеств, в которой принадлежность элемента ко множеству носит оценочный характер.

Основные операции классической (аристотелевой) логики § § § Конъюнкция (логическое И). a/b=истина, если а=истина и b=истина; во всех остальных случаях – ложь Дизъюнкция (логическое ИЛИ). a/b=истина, если истинно либо a, либо b, либо оба. Отрицание (логическое НЕ). ¬a=истина, если а – ложь, и наоборот. Эквивалентность a b. Истинна, если а и b одинаковы (эквивалентны), иначе – ложь. Импликация (когда a, то b). ¬a/b. a считается посылкой, b – следствием. Ложна только если посылка истинна, а следствие ложно. Т. е. , если посылка истинна, то для истинного результата должно быть истинно и следствие. Если посылка ложна, то следствие не имеет значения, результат всё равно будет истинным.

Нечёткая логика § В нечёткой логике значение логических переменных и результат логических операций лежит в пределах 0… 1. § Меняется определение логических операций: конъюнкция определяется либо как минимум двух операндов, либо как их произведение; дизъюнкция – либо как максимум, либо как сумма за вычетом произведения. Отрицание – вычитание из единицы.

Области систем нечёткой логики § Работа с неполной, неточной информацией § Анализ словесных и качественных описаний § Работа с нечёткими множествами

Основы теории множеств § Множество - это набор некоторого количества (нулевого, конечного, бесконечного) определённых элементов. § Элементы множества могут определяться перечислением (только для конечных множеств), а могут задаваться функцией принадлежности Р(х). Множество А={x | P(x)} может быть образовано только тогда, когда из истинности P(x) следует, что х ∈ A. Для теории множеств существует ряд аксиом, а также операции: § Принадлежности § Содержания § Объединения § Пересечения § Разности § Дополнения § Симметрической разности

Нечёткие множества § § § § § Нечётким называют множества, функция принадлежности к которому принимает значения от 0 до 1 (нецелые). Как правило, операция принадлежности вводится для элементов универсального множества Х. Для каждого элемента х ∈ Х определена функция принадлежности ко множеству А как 0≤μ(х)≤ 1. Носителем множества А называют такое множество элементов х, для которых μ(х)>0. Высотой множества А называют максимальное значение μ(х) на множестве А. Если высота равна 1, такое множество называют нормальным, в противном случае оно субнормально. Операция содержания для нечётких множеств изменяется: А ⊂ В, если для любого значения х ∈ Х значение μА(х)≤ μВ(х) Множества считаются равными, если для любого х ∈ Х μА(х) = μВ(х) Для каждого нечёткого множества А существует α-срез: такое чёткое множество Аα, которое содержит только те элементы х, для которых μ(х) ≥ α Пересечение нечётких множеств – наибольшее множество, содержащееся в обоих Объединение нечётких множеств – наименьшее множество, содержащее оба множества Произведение нечётких множеств – такое множество, для каждого элемента которого функция принадлежности

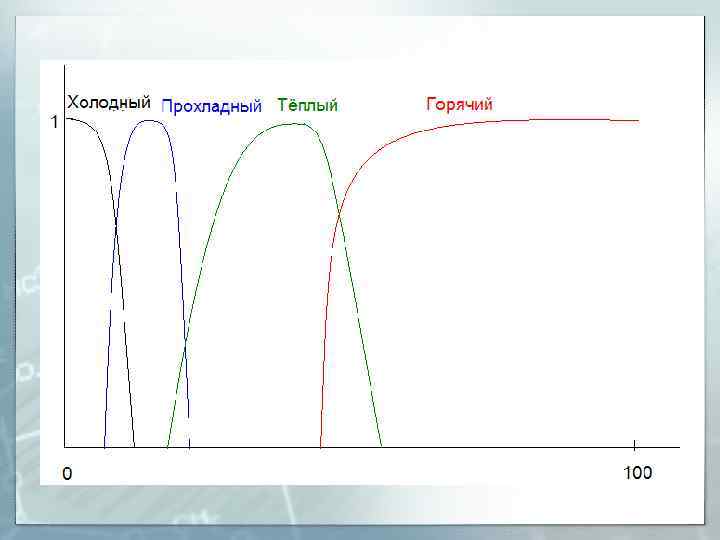
Лингвистические (нечёткие) переменные § Переменные, выражаемые словесно и используемые для суждений, могут быть описаны методами нечёткой логики. § Примеры значений лингвистических переменных: «очень долгий процесс» , «высокая температура» , «приятный вкус» . § Лингвистическая переменная характеризуется следующими свойствами: § Названием х § Множеством словесных значений переменной Т(х), каждое из которых – нечёткая переменная § Х – множество числовых значений для Т(х) § G – синтаксическое правило для образования новых значений § М – математическое правило, определяющее вид функции принадлежности. Пример: § x – температура продукта § Т(х) – «холодный» , «прохладный» , «тёплый» , «горячий» § Х – значение температуры в градусах Цельсия § § G – «очень» , «не очень» . М – функция принадлежности

Применение нечёткой логики и нечётких множеств в оптимизации § Задачи нечёткой логики, в первую очередь, важны на первом этапе – этапе получения входных данных. § На основании словесных оценок (дегустаторов, экспертов, испытателей) и разработанной функции соответствия получают числовое значение переменной (как правило, фактора). § Далее решают задачу оптимизации классическим способом. § В ряде случаев нечёткую логику используют для построения параметра оптимизации: по словесным оценкам экспертов, каким должен быть продукт, находят параметры оптимизации, выбирают их эталонные значения.

Альтернативные подходы к формированию целевых функций. 1. Функция потерь Таруги x 0 – эталонное значение параметра; х – фактическое значение параметра; с – коэффициент пропорциональности. Достоинства: § Позволяет оптимизировать процесс, устремляя параметр к эталону § При больших отклонениях функция потерь имеет очень большое значение. § Очень хорошо подходит при решении задачи унификации Недостаток: Должен быть очень точно определён эталон; в случае, когда выбор эталона несёт частично произвольный или приблизительный характер, и задачи унификации не ставится, оказывается слишком затратным поддержание минимально возможного отклонения.

Функция желательности Харрингтона § § § Основана на переводе параметра оптимизации к виду шкалы от 0 до 1 и соответствующим словесным оценкам: 0, 8 … 1 – очень хорошо; 0, 63 … 0, 8 – хорошо; 0, 37 … 0, 63 – удовлетворительно; 0, 2… 0, 37 – плохо; 0… 0, 2 – очень плохо. Для перевода служит функция d = exp(-y)). При этом сам параметр оптимизации необходимо максимизировать; он может меняться на всём диапазоне действительных чисел. Комплексный показатель желательности рассчитывают по формуле (n – число параметров):

Метод множителей Лагранжа §

Решение задач классификации с целью оптимизации Задачи классификации получили широкое распространение в научных исследованиях, в том числе и в прикладной науке. В рамках оптимизации они играют вспомогательную роль: § С целью сокращения факторного пространства. Целый ряд факторов можно заменить порядковым номером класса. § С целью замены оптимального (по определённым параметрам) решения на близкое к оптимальному, но удовлетворяющее дополнительным условиям (доступность сырья, замена режима обработки) § С целью отсева из дискретного набора явно неоптимальных вариантов и последующей оптимизации в пределах наилучшего класса. С другой стороны, большинство методов классификации сами по себе используют процесс оптимизации.

Классификация § Классификация – это разделение объектов на группы (классы) в соответствии с некоторыми признаками. § Классификация может проводиться по заранее заданным строгим правилам. В этом случае задача классификации считается корректно поставленной, решается достаточно просто, однако границы между классами могут оказаться условными, таким образом, различие в пределах одного класса окажется сильнее, чем между соседними классами. § В ряде случаев правила классификации подбираются специально, чтобы получить максимально разделённые классы. § Если набор правил имеет сложный характер или классификация сложилась традиционно (а вопрос классификации новых объектов открыт), то используют методы дискриминантного анализа, в т. ч. на основе ИНС. Задачей дискриминантного анализа является поиск переменных, наилучшим образом разделяющих классы. § В случае, когда правил не создано, но необходимо разбить данные на классы, помощь может оказать метод кластерного анализа.

Кластерный анализ § § § Кластерный анализ (кластеризация) – это совокупность методов, позволяющих разбить серию данных, представляющую совокупность признаков (факторное пространство) на отдельные группы (классы, кластеры), близкие между собой по значениям признаков. Кластеризация является одной из некорректно поставленных задач и одним из вариантов «обучения без учителя» . Кластеризация фактически предоставляет исследователю материал, гипотезу для дальнейшей проверки. Кластерный анализ не гарантирует правильное распределение данных по уже имеющимся классам

Методы кластеризации Большинство методов кластерного анализа предполагает, что число классов задаётся изначально. Наиболее распространены следующие методы: § Метод k-средних (k-mean), k-медиан. § Метод формальных элементов. § Метод нечётких множеств (C-средних) § Генетический алгоритм § Объединительные алгоритмы, графовый подход

Метод k-средних § § § § Ключевым положением является измерение дистанции между элементами и между кластерами. Первоначально весь набор данных разделяют между кластерами случайно. Внутри каждого кластера центр масс (центральную точку). Рассчитывают суммарное расстояние каждого элемента в каждом кластере от центра масс этого кластера Суммируют такие расстояния по всем кластерам. Иногда при наличии пустых классов и классов с одним элементом добавляется «штраф» . Такая сумма (KM-сумма) будет мерой эффективности кластеризации (её необходимо минимизировать). Случайным образом выбирается кластер и элемент в нём (иногда – самый «далёкий» от центра), а также второй кластер. Элемент временно переносится из первого кластера во второй, проверяется KM-сумма и, если она увеличилась, шаг признаётся неудачным, всё возвращается на место. Если она уменьшилась, то шаг считается удачным, поиск ведут дальше. Процесс останавливают, если длительное время удачный шаг найти не получается. При этом невозможно гарантировать, что данный вариант кластеризации является глобальным, а не локальным оптимумом.

Графовый подход, объединительные методы § § Объединительные методы предполагают объединение отдельных кластеров между собой. Графовый подход предполагает то же самое действие, только схематично оно может быть представлено в виде графа, в котором каждый кластер включает в себя подкластеры. Определяются два наиболее близких элемента и объединяются между собой в кластер. Процесс продолжают, объединяя между собой как отдельные элементы, так и кластеры (или кластер с отдельным элементом). Расстояние между кластерами определяется как расстояние между их центрами масс. Процесс продолжают, пока число кластеров не уменьшится до требуемого

Метод формальных элементов (FOREL) § § Метод основан на поиске локальных сгущений. В данном методе вокруг случайного элемента создают окружность (сферу, гиперсферу) определённого радиуса. Все элементы, попавшие в эту гиперсферу, образуют новый кластер. Рассчитывают его центр масс и в нём строят новую гиперсферу, вероятно, захватывая другие элементы. Тем временем, элементы, попавшие в кластер случайно, в таком случае покинут кластер. Как только центр масс не меняется, кластер считается стабилизированным, все элементы убираются из дальнейшей кластеризации.

Оптимизация рецептур в общественном питании (общая методика) § § § § § Проводится серия поисковых работ для определения направления исследования. Определяются параметры оптимизации (объективные и субъективные). При наличии параметров, устремляемых к некоторому оптимуму, проводится поиск оптимума (регрессионный анализ). Определяются коэффициенты значимости (экспертный метод) и формируется целевая функция. Проводится поиск влияющих факторов. При необходимости выявляются наиболее значимые, сужается факторное пространство. Все влияющие факторы, кроме выбранных, фиксируются на постоянном уровне. Составляется план эксперимента, проводится его рандомизация. Проводится эксперимент в соответствии с планом. Проводится регрессионный анализ, получается уравнение регрессии. Определяется оптимальное значение в данном диапазоне. Если значение находится на границе диапазона, необходимо либо расширить диапазон, либо доказать, что дальнейшее движение нецелесообразно или невозможно.

Дальнейшие шаги по оптимизации § § Уточнение значения оптимума с помощью ЦРКП вблизи найденной точки. Попытка расширения диапазона варьирования факторов (особенно в случае признаков оптимума за границами диапазона) Поиск оптимума по ранее не варьируемым факторам (в т. ч. замена сырья). Модификация целевой функции в свете возникших проблем оптимизации.

Скачать презентацию Оптимизация технологических и процессов общественного питания 18 ч

Оптим.pptx

Количество слайдов: 77