Оптимизационные задачи электроэнергетики 1 Технические и технико

Оптимизационные задачи электроэнергетики 1

Технические и технико - экономические задачи, решаемые при проектировании выбор структуры генерирующих мощностей ; размещение электростанций и их развитие во времени ; выбор конфигурации сети : сравнение экономичности вариантов; 2

Технические и технико - экономические задачи, решаемые при проектировании проведение оптимизационных расчетов экономически целесообразной компенсации реактивной мощности ; конструкторские расчеты проводов, опор и других сооружений, расчеты трасс ЛЭП переработка оперативной информации ; 3

Технические и технико - экономические задачи, решаемые при проектировании определение допустимой области управления ; оптимизация режимов; 4

Оптимальное решение – наилучшее из всех допустимых Оптимизация - процесс поиска оптимального решения – Оптимизационные задачи – задачи, в которых ищется оптимальное решение. Методы математического программирования – математические методы, предназначенные для решения оптимизационных задач 5

Критерий оптимальности – показатель, по величине которого оценивают, является ли решение оптимальным Экономический критерий - минимум затрат на реализацию поставленной задачи. 6

Критерии оптимальности критерий надежности электроснабжения; критерий качества электроэнергии; критерий наименьшего отрицательного воздействия на окружающую среду (экологический критерий). 7

Достижение максимальной мощности вырабатываемой энергии (любого вида) при заданных энергоресурсах. Достижение максимума экономической эффективности суммарной выработанной энергии Минимизация затрат на строительство объектов энергетики на основе ресурсов региона 8

Этапы решения оптимизационной задачи 1. Сбор исходной информации. 2. Составление математической модели, под которой понимается формализованное математическое описание решаемой задачи. 3. Выбор метода решения, определяемого видом математической модели. 9

Этапы решения оптимизационной задачи 4. Выполнение математических вычислений. 5. Анализ решения задачи. 10

Исходная информация определенная или детерминированная случайная неопределенная или недетерминированная 11

Математическая модель целевую функцию; ограничения; граничные условия 12

Целевая функция математическая запись критерия оптимальности Z(х1, х2, . . . хn)→ extr х1, х2, . . . хn – искомые переменные, значения которых вычисляются в процессе решения задачи 13

Перемнные непрерывные дискретные целочисленные 14

Ограничения f 1(х1, х2, . . . хn)< b 1; f 2(х1, х2, . . . хn) = b 2; . . fm(х1, х2, . . . хn) > bm. 15

Граничные условия di <= хi <= Di, i=1, 2, … n di и. Di - соответственно нижняя и верхняя границы диапазона изменения переменной xi 16

Методы решения оптимизационных задач методы математического программирования - многократно повторяющаяся вычислительная процедура, приводящая к искомому оптимальному решению 17

методы линейного программирования используют при линейных зависимостях между переменными методы нелинейного программирования используют при нелинейных зависимостях между переменными 18

методы целочисленного программирования используют при целочисленных переменных методы дискретного программирования используют при дискретных переменных 19

Анализ решения оптимизационной задачи Параметрический анализ – анализ, при котором задача решается многократно при различных значениях некоторого исходного данного (параметра). Оценивается влияние этого параметра на результаты решения. 20

Анализ решения оптимизационной задачи Структурный анализ – анализ, при котором многократное решение задачи выполняется при различной структуре ограничений и граничных условий. Оценивается влияние ограничений и граничных условий на результаты решения. 21

Анализ решения оптимизационной задачи Многокритериальный анализ – анализ, при котором проводится решение задачи по различным критериям (с различными целевыми функциями) 22

ТРАНСПОРТНЫЕ ЗАДАЧИ ЭЛЕКТРОЭНЕРГЕТИКИ 23

Постановка транспортной задачи Транспортная задача - это задача отыскания таких путей перевозки продукта от пунктов производства к пунктам потребления, при которых общая стоимость перевозок оказывается минимальной. 24

продукт – электрическая мощность, передаваемая от источников питания к потребителям по линиям электропередачи источники питания – электрические станции или подстанции, потребители – промышленные, городские, сельскохозяйственные потребители электроэнергии. Оптимизации подлежат затраты на схему электрической сети, состоящей из линий электропередачи, связывающих узлы источников питания с узлами потребителей 25

Пусть в проектируемой системе электроснабжения имеется i =1, 2, . . . n узлов источников питания и j = 1, 2, . . . m узлов потребителей. Мощность каждого из источников составляет Ai, а мощность каждого из потребителей -Bj единиц мощности (е. м. ). Известно взаимное расположение узлов источников и потребителей. Стоимость передачи единицы мощности от источника i к потребителю j (удельная стоимость) составляет zij у. е. /е. м. 26

Общее количество возможных к строительству линий электропередачи, связывающих источники с потребителями, составляет nm. Мощности, передаваемые по этим линиям, являются искомыми переменными xij, следовательно, количество искомых переменных составляет nm. Затраты на электрическую сеть равны сумме произведений удельных стоимостей на величины передаваемых мощностей от источников i к потребителям j. 27

28

Особенности транспортной задачи все ограничения имеют форму равенств; все коэффициенты при переменных в системе ограничений равны плюс единице; каждая переменная дважды входит в систему ограничений: один раз в балансы узлов источников, второй раз в балансы узлов потребителей 29

В проектируемой системе электроснабжения имеется два узла с источниками питания и три узла потребителей. Мощности источников составляют. A 1 и. А 2, а мощности потребителей -B 1, В 2 и. В 3 е. м. 30

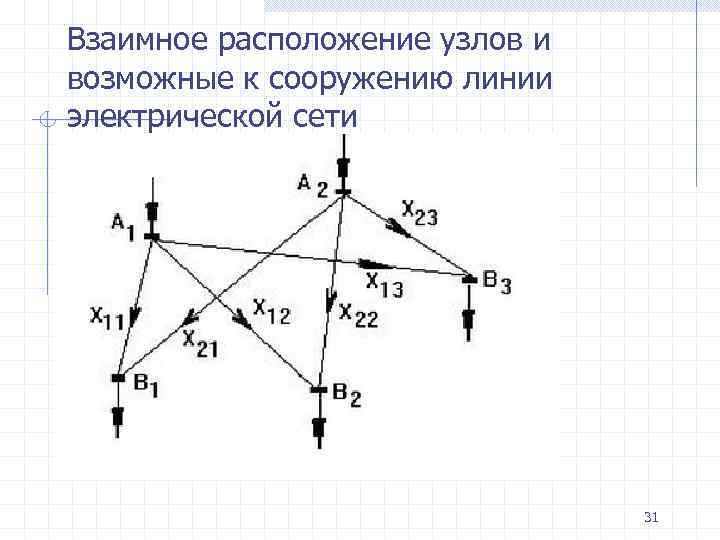Взаимное расположение узлов и возможные к сооружению линии электрической сети 31

Удельные затраты на передачу мощностей по линиям между узлами источников и потребителей составляют z 11, z 12, z 13, z 21, z 22, z 23 у. е. /е. м. Составить математическую модель для решения транспортной задачи. 32

Целевая функция, представляющая собой суммарные денежные затраты на электрическую сеть, в соответствии выражением (1) будет иметь вид Z=z 11 x 11+z 12 x 12+z 13 x 13+z 21 x 21+z 22 x 22+z 23 x 23→min 33

Ограничения, представляющие собой балансы мощности в узлах электрической сети, в соответствии с выражениями (2) и (3) будут иметь следующий вид: x 11+x 12+x 13=A 1, x 21+x 22+x 23=A 2, x 11+x 21=B 1, x 12+x 22=B 2, x 13+x 23=B 3. 34

Граничные условия в соответствии с соотношением (4) запишутся x 11>0, x 12>0, x 13>0, x 21>0, x 22>0, x 23>0. 35

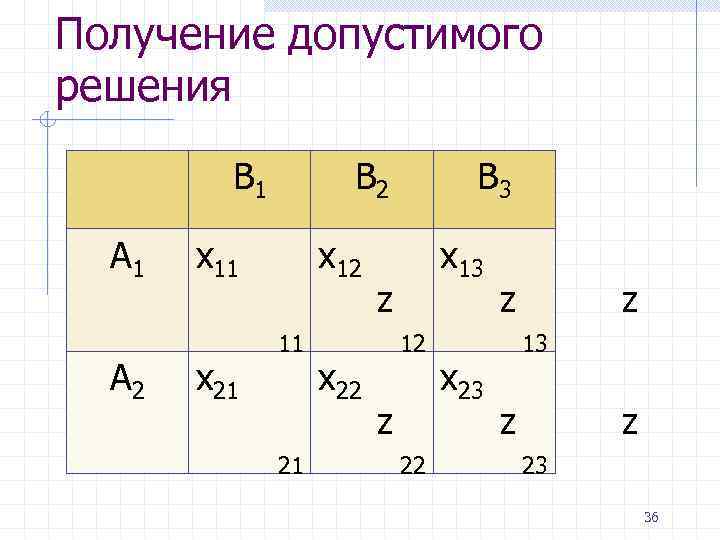Получение допустимого решения B 1 A 2 x 11 x 21 B 2 B 3 x 12 x 13 z z 11 12 13 21 22 23 x 22 x 23 z z 36

Алгоритм минимальной удельной стоимости 1. В транспортной матрице выбирается клетка с минимальным значением zij. Если имеется несколько таких клеток, то выбирается любая из них. 37

2. В выбранную клетку в качестве базисной переменной заносится наименьшая из двух величин Ai или. Bj , т. е. xij = min(Ai, Bj). При этом выполняется баланс мощности по строке i или столбцу j, в которые входит переменная xij. 38

3. В остальные клетки строки i или столбца j , для которых выполнен баланс мощности, заносятся нули, соответствующие свободным переменным. Большая из двух величин Ai и. Bj условно заменяется разностью этих двух величин. 39

4. Из оставшихся незаполненных клеток транспортной матрицы вновь выбирается клетка с минимальным значением zij. 5. Далее пункты 2 и 3 повторяются до полного заполнения всех клеток транспортной матрицы. 40

общее количество переменных составляет nm. Количество отличных от нуля базисных переменных составляет (n+m-1). Количество равных нулю свободных переменных составляет (nm-(n+m-1)). 41

Метод потенциалов 1. Проверяют выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводят фиктивный источник питания или потребителя с недостающими мощностями и нулевыми удельными затратами. 42

2. Строят начальное опорное решение (методом минимальной стоимости) и проверяют правильность его построения, для чего подсчитывают количество занятых клеток (их должно быть m+n-1). 43

3. Строят систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений ui + vj = zij при xij>0. Для того чтобы найти частное решение системы, одному из потенциалов (обычно тому, которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще нуль). 44

Остальные потенциалы однозначно определяются по формулам ui = zij - vj если известен потенциал vj vi = zij - uj если известен потенциал uj 45

4. Проверяют, выполняется ли условие оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам Δik = ui + vj - zij те оценки, которые больше нуля, записывают в левые нижние углы клеток. 46

Если для всех свободных клеток Δij<=0, то вычисляют значение целевой функции, и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, то опорное решение не является оптимальным. 47

5. Переходят к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка max{Δij}= Δik. 48

Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-» , начиная с «+» в клетке с наибольшей положительной оценкой. 49

Осуществляют сдвиг (перераспределение мощности) по циклу на величину θ= min{xij}. Клетка со знаком «-» , в которой достигается min{xij}, остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m+n-1. Далее возвращаемся к пункту 3 алгоритма. 50