88f877cdb9f0f559c25ea8a7f299f43b.ppt
- Количество слайдов: 18

Optimal Inter-Object Correlation When Replicating for Availability Haifeng Yu National University of Singapore Phillip B. Gibbons Intel Research Pittsburgh Haifeng Yu (National University of Singapore)

Multi-object Operations § Data replication for better availability § Traditional research focuses on availability of individual data objects § E. g. , individual files or database objects § User-level tasks may access multiple data objects / files: Multi-Object Operations § Compile a project / Latex a paper § Aggregation queries for databases Haifeng Yu (National University of Singapore) 2

Availability of Multi-Object Operations § Availability of single object is not the same as the availability for multi-object operations: § An operation requesting 1, 000 objects may observe nearly 1, 000 times higher failure probability § But there’s more. . . § Our recent experimental study shows that the assignment from object replicas to machines has critical effects on such availability: “Availability of Multi-Object Operations” [NSDI’ 06] Haifeng Yu (National University of Singapore) 3
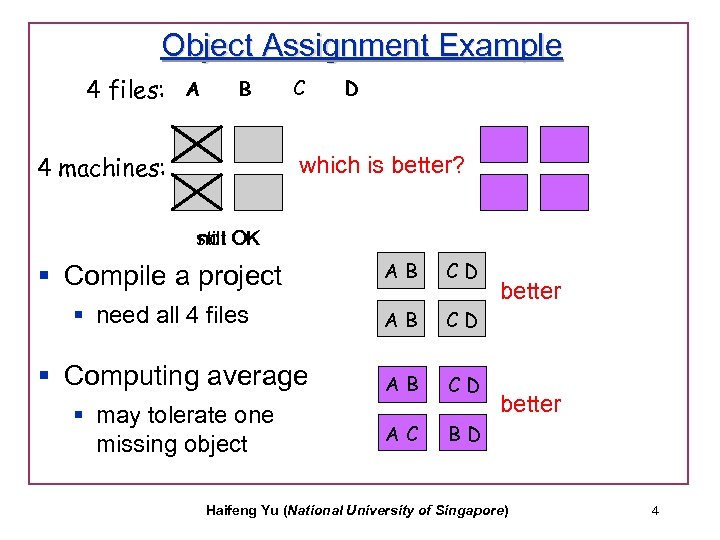
Object Assignment Example 4 files: A B 4 machines: C D which is better? not still OK § Compile a project AB CD § need all 4 files AB CD § Computing average AB CD § may tolerate one missing object AC BD better Haifeng Yu (National University of Singapore) 4

Important Observations from the Example AB CD which is better? AB CD AC BD § For individual objects, it does not matter which machines it is assigned § Distinguishes from replica placement problems § Same “concentration” / “spread” § Difference is in inter-object correlation: § Obj A is “fully correlated” with one obj (B) VERSUS § Obj A is “partially correlated” with two objs (B and C) Haifeng Yu (National University of Singapore) 5

Practical Importance § Applicable to almost all replication systems § CAN, CFS, Chord, Coda, FARSITE, GFS, GHT, Glacier, Pastry, R-CHash, RIO, … § Failure probability of TPC-H varies by 4 orders of magnitude under different assignments § All with the same storage overhead 6

Formal Model § N objects each with k replicas § Each machine holds l objects (total Nk / l machines) § Machines fail / crash i. i. d. § Object unavailable if all k machines holding it fail § Assignment: Mapping from objects to machines § No machine holds multiple replicas of the same obj § Two specific assignments: § PTN: Partition objects into N/l groups of size l, and map each group to k machines § RAND: A uniformly random assignment Haifeng Yu (National University of Singapore) 7

Formal Model (continued) § A multi-object operation requests n specific objs § This talk assumes n = N; See paper for n < N. § Operation is successful if ≥ t objects are available § t depends on application semantics § We will consider a single (multi-object) operation § See paper for more discussion on this… § Availability of the assignment defined as § Prob[the operation succeeds] Haifeng Yu (National University of Singapore) 8
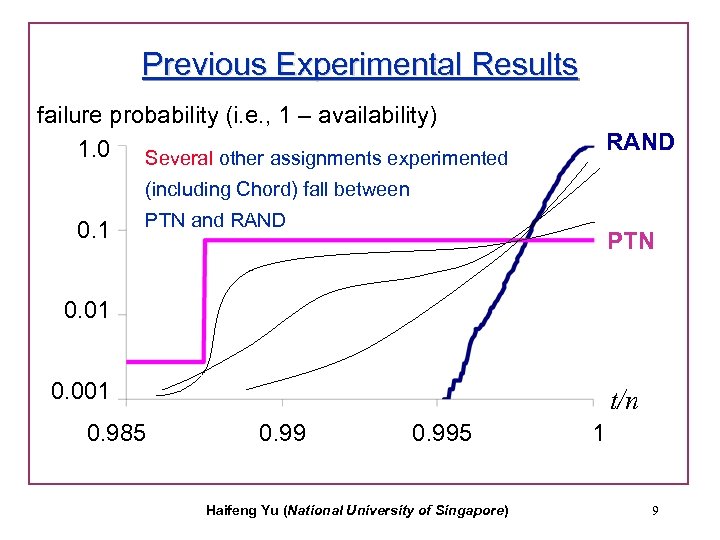
Previous Experimental Results failure probability (i. e. , 1 – availability) 1. 0 Several other assignments experimented RAND (including Chord) fall between 0. 1 PTN and RAND PTN 0. 01 0. 001 0. 985 t/n 0. 995 Haifeng Yu (National University of Singapore) 1 9

Our Goal § Limitations of experimental method: § Can only study a small number of assignments § Results only for specific parameter values (e. g. , specific machine failure probabilities) § Our goal: § Find assignment with best/worst availability among all possible assignments § This is the first theoretical study on this subject… Haifeng Yu (National University of Singapore) 10
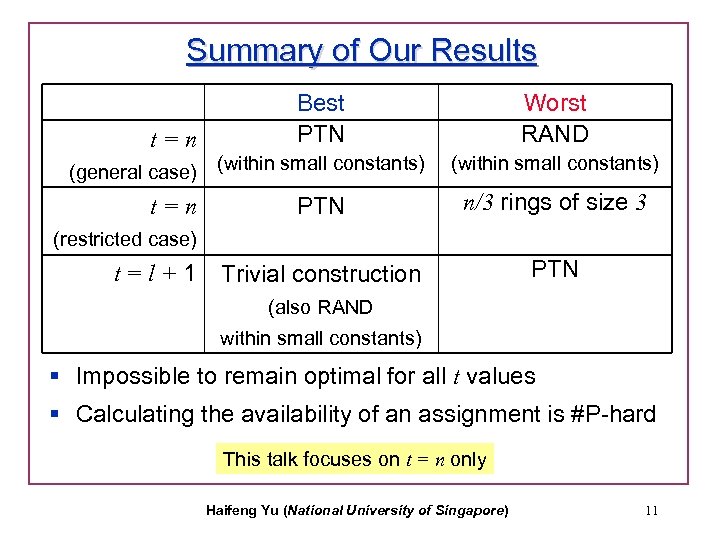
Summary of Our Results t=n (general case) t=n Best PTN Worst RAND (within small constants) PTN n/3 rings of size 3 Trivial construction PTN (restricted case) t=l+1 (also RAND within small constants) § Impossible to remain optimal for all t values § Calculating the availability of an assignment is #P-hard This talk focuses on t = n only Haifeng Yu (National University of Singapore) 11

The General Case § Upper and lower bounds § Leveraging Janson’s inequality – a tail approximation for sum of dependent Bernoulli trials Not to be confused with Jensen’s inequality § Approaching upper and lower bounds by PTN and RAND § Leverage Janson’s inequality a second time § See paper for details… Haifeng Yu (National University of Singapore) 12

The Restricted Case § Results for general case § Have constants § RAND is a distribution – what is the “structure” of the worst assignment? § We consider significantly restricted scenarios § Each object has two replicas § Each machine holds two objects (l = 2) § Corresponds to our example earlier Haifeng Yu (National University of Singapore) 13
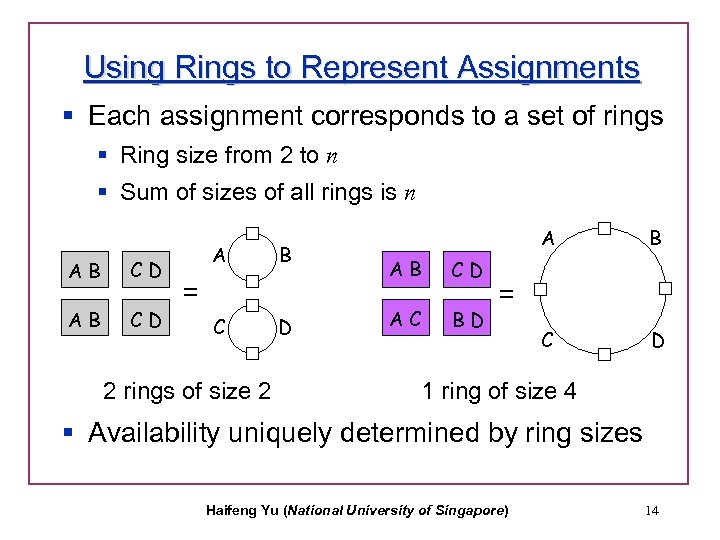
Using Rings to Represent Assignments § Each assignment corresponds to a set of rings § Ring size from 2 to n § Sum of sizes of all rings is n AB CD A B = C 2 rings of size 2 D A AB CD AC BD B C D = 1 ring of size 4 § Availability uniquely determined by ring sizes Haifeng Yu (National University of Singapore) 14

Hill Climbing § Adjustment step: merge two rings into one or split one ring into two § Can always transform an assignment to another within a finite number of steps § Crux: How does availability change when merging two rings of size x and y (x y) into a ring of size (x+y) ? § Theorem: Availability improves iff y is odd. Haifeng Yu (National University of Singapore) 15

The Restricted Case: Results § Theorem: n/2 rings of size 2 is the best. § This corresponds to PTN § Theorem: n/3 rings of size 3 is the worst. § What about a single ring of size n? § What about rings of other sizes? § See paper for answers… § Parity of ring sizes matter a lot… Haifeng Yu (National University of Singapore) 16
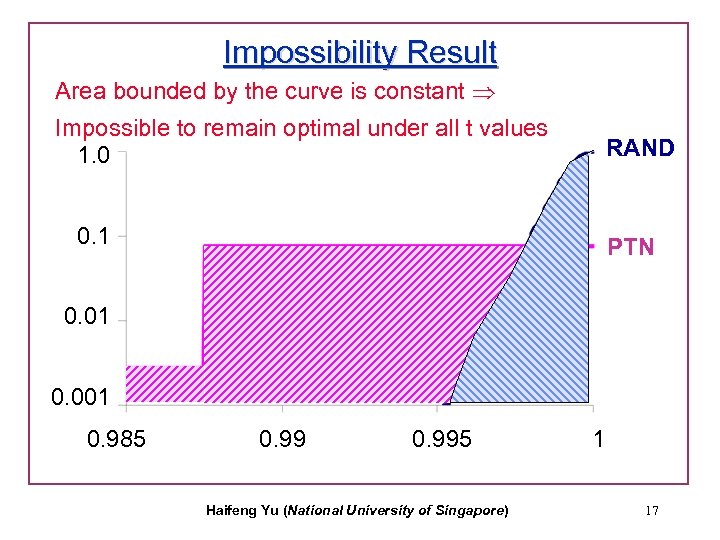
Impossibility Result Area bounded by the curve is constant Impossible to remain optimal under all t values 1. 0 RAND 0. 1 PTN 0. 01 0. 001 0. 985 0. 995 Haifeng Yu (National University of Singapore) 1 17

Conclusions § Availability of multi-object operation critically affected by inter-object correlation § First theoretical study of object assignment § Best/worst assignments for t = n and t = l + 1 § Impossible to remain optimal under all t values § See paper for full results… § Open questions: § Other t values? § Erasure coding? Haifeng Yu (National University of Singapore) 18
88f877cdb9f0f559c25ea8a7f299f43b.ppt