Optimal Algorithms for k-Search with Application in Option

Optimal Algorithms for k-Search with Application in Option Pricing Julian Lorenz, Konstantinos Panagiotou, Angelika Steger Institute of Theoretical Computer Science, ETH Zürich 15. 05. 2007

Online Problem k-Search (1/2) 4$ 9$ 5$ 1$ k-max-search : k-min-search : Player wants to sell k³ 1 units for MAX profit Player wants to buy k³ 1 units for MIN cost • Prices =(p 1, …, pn) presented sequentially • Must decide immediately whether or not to buy/sell for pi • Competitive analysis: 09. 10. 2007 (MAX profit (MIN cost) ) Julian Lorenz, jlorenz@inf. ethz. ch

Online Problem k-Search (2/2) Model for price sequences : M § pi Î [m, M], arbitraryin that trading range § M = m j, fluctuationratio j > 1 § Can buy/sell only one unitfor each pi § Length of known in advance 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch m i

Related Literature El-Yaniv Fiat, Karp, Turpin (2001): , § Timeseries-Search: Optimal deterministic (=1 -max-search) Optimal randomized § One-Way-Trading: Optimal algorithm & no improvement by randomization One-Way-Trading: Can trade arbitrary fractions for each pi Other related problems : § Search problems with distributional assumption on prices § Secretary problems 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Deterministic Search Algorithms 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

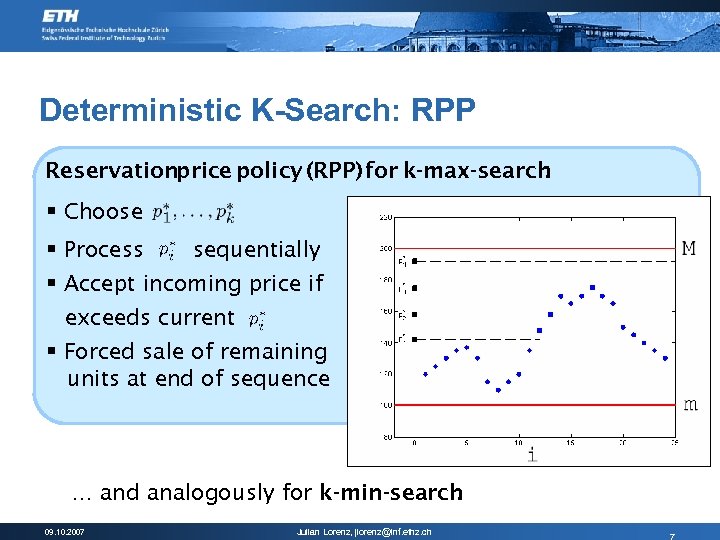Deterministic K-Search: RPP Reservationprice policy (RPP) for k-max-search : § Choose § Process sequentially § Accept incoming price if exceeds current § Forced sale of remaining units at end of sequence … and analogously for k-min-search. 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Theorem: Deterministic K-Max-Search 50 RPP with where 45 40 solution of 35 30 p i 25 20 15 i) Optimal RPP with competitive ratio 10 5 10 ii) Optimal deterministic online algorithm for k-max-search i Remarks : 1) Asymptotics: 2) “Bridging“ Timeseries-Search and One-Way-Trading 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch 15

Theorem: Deterministic K-Min-Search 50 RPP with where 45 40 solution of 35 30 pi 25 20 15 i) Optimal RPP with competitive ratio 10 5 10 ii) Optimal deterministic online algorithm for k-min-search i Remarks : Asymptotics: 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch 15

Randomized Search Algorithms 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Randomized k-Max-Search Consider k=1: Optimal deterministic RPP has . Randomizedalgorithm. EXPO: Fix base. Choose random, set RP to. Competitive ratio uniformly at (El-Yanivet. al. , 2001). We can prove: In fact, asymptotically optimal. 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Theorem: Randomized K-Max-Search For any randomized k-max-search algorithm RALG, the competitive ratio satisfies Remarks : 1) Independent of k 2) Algorithm EXPO achieves k EXPO : k Set all k reservation prices to 3) Small k 09. 10. 2007 significant improvement! ( Julian Lorenz, jlorenz@inf. ethz. ch . )

Theorem: Randomized K-Min-Search For any randomized k-min-searchalgorithm RALG, the competitive ratio satisfies Remarks : 1) Again independent of k 2) No improvementover deterministic. ALG possible! Recall CR of RPP for k-minsearch 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Yao‘s Principle (mincost online problems) § § Finitely many possible inputs Set of deterministic algorithms RALG any randomized algorithm f( ) any fixed probability distribution on Then: With respect to f( ) ! Best deterministic algorithm for fixed input distribution 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch Lower bound for best randomized algorithm

On the Proof of Lower Bound For k-min-search k=1: , f( ) uniform distribution on Essentially only two deterministicalgorithms : § ALG 1 buys at § ALG 2 rejects , hoping that next quote is Similarly for arbitrary k, and for k-max-search … 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Application To Option Pricing 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Application: Pricing of Lookback Options Two examples of options (there all kinds of them…): • European Call Option: right to buy shares for prespecified price at future time T from option writer • Lookback Call Option: right to buy at time T for minimum price in [0, T] (i. e. between issuance and expiry) Option price (“premium“) paid to the option writer at time of issuance. Fair Price of a Lookback Option? 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Classical Option Pricing: Black Scholes • Model assumption for stock price evolution Geometric Brownian. Motion: • No-Arbitrage and pricing by “replication“: Riskless. Replication Trading algorithm (“hedging“) for option writer to meet obligation in all possible scenarios. No-Arbitrage. Assumption(“efficientmarkets “) “Hedging cost“ must be option price. Otherwise: Arbitrage (“free lunch“). 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Drawback of Classical Option Pricing What if Black Scholes model assumptionsno good? In fact, in reality L price ¹ geometric Brownian motion L trading not continuous L … De. Marzo Kremer, Mansour (STOC’ 06): , Bounds for European options using competitive trading algorithms Weaker model assumptions 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch „Robust“ bounds for option price

Bound for Price of Lookback Call Hedging lookback call = buying “close to min“ in [0, T] _ Use k-min-search algorithm! _ Hedging cost = comp. ratio of k-minsearch = option price Instead of GBM assumption : • Trading range • Discrete-time trading Robust bound for option price, qualitatively and quantitatively similar to Black Scholes price V = price of lookback call on k shares Under no-arbitrage assumption 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch

Thank you very much for your attention! Questions? 09. 10. 2007 Julian Lorenz, jlorenz@inf. ethz. ch