ОПТИЧЕСКИЕ СОЛИТОНЫ Лекция 4 Дискретные пространственные солитоны В

ОПТИЧЕСКИЕ СОЛИТОНЫ (Лекция 4) Дискретные пространственные солитоны В. М. Шандаров Томский государственный университет систем управления и радиоэлектроники

Определения • Дискретная дифракция – дифракционное изменение светового поля в системе связанных оптических волноводов, обусловленное эффектами туннельной связью элементов волноводной системы. • Фотонная решетка (photonic lattice, waveguide array) – система связанных оптических волноводов. Может быть одномерной, двумерной, регулярной или нерегулярной. • Дискретный солитон – нелинейный бездифракционный режим распространения светового поля в фотонных решетках.

Система связанных оптических волноводов Waveguide Array Fields Coupling due to Field Overlap

Дифракция света в однородной среде и в фотонных решетках W 0 θ Угловая расходимость гауссова пучка: θ ≈ λ/W 0 λ – длина волны света; W 0 – ширина пучка в перетяжке Дискретная дифракция в периодической структуре при возбуждении одного волновода Distance

Дифракция света в фотонных решетках где - En амплитуда поля в n – том элементе; b - постоянная распространения волноводной моды в изолированном элементе; z – продольная координата; С – коэффициент связи; учитывает эффект нелинейно-оптического самовоздействия светового поля (в данном случае оно соответствует керровской нелинейности среды).

Линейная дискретная дифракция света В линейном случае дифракционные эффекты в периодической системе описываются уравнением: (*) Его аналитическое решение имеет вид плоской волны: где плоскости волноводных элементов перпендикулярны оси x; kx и kz – поперечная и продольная составляющие волнового вектора плоской световой волны. Подставив это выражение в (*), получим дисперсионное уравнение, описывающее связь между компонентами kx и kz:

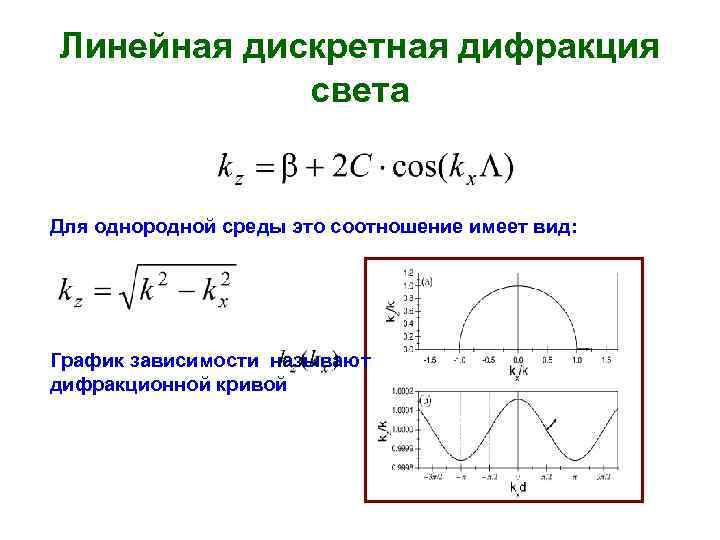Линейная дискретная дифракция света Для однородной среды это соотношение имеет вид: График зависимости называют дифракционной кривой

Линейная дискретная дифракция света Для характеристики дифракции в периодической волноводной системе вводится дифракционный параметр Из соотношения получим: Отсюда следует, что при |kx. L|

p/2. Интервал значений |kx. L|

Линейная дискретная дифракция света Области |kx. L|

p/2 называют областями нормальной и аномальной дифракции, поскольку первой соответствует выпуклый участок дифракционной кривой, как и в случае однородной среды, а второй вогнутый. При |kx. L|=p/2 параметр D=0 и распространение светового пучка в направлении, задаваемом данным условием, характеризуется отсутствием дифракции.

Линейная дискретная дифракция света Особенностью периодических волноводных систем является то, что при переходе из области нормальной в область аномальной дифракции оптическая нелинейность системы меняет знак. Это дает принципиальную возможность формирования, например, светлых пространственных солитонов в среде с самодефокусирующей нелинейностью, при распространении света в области аномальной дифракции. И наоборот, в среде с самофокусирующей нелинейностью в области аномальной дифракции могут формироваться темные пространственные солитоны.

Линейная дискретная дифракция света В случае бесконечного числа волноводных элементов и одинаковой связи между соседними волноводами, при возбуждении света на входе структуры только в одном канале, распределение амплитуды поля по элементам определяется соотношением: где n – номер элемента (свет возбуждается в элементе с n=0, а при n≠ 0); z – расстояние от входа структуры в направлении распространения света; i – мнимая единица; Jn – функция Бесселя n-го порядка.

Линейная дискретная дифракция света Примеры картин светового поля в ФР при возбуждении нескольких элементов (а), одного элемента (b) и нескольких элементов при распространении света в направлении, для которого D=0 (c).

Дискретные пространственные солитоны

Дискретные пространственные солитоны (1 ый эксперимент)

Дискретные пространственные солитоны (1 ый эксперимент)

Дискретные пространственные солитоны (SBN)

Дискретные пространственные солитоны (SBN)

Дискретные пространственные солитоны (Li. Nb. O 3: Ti)

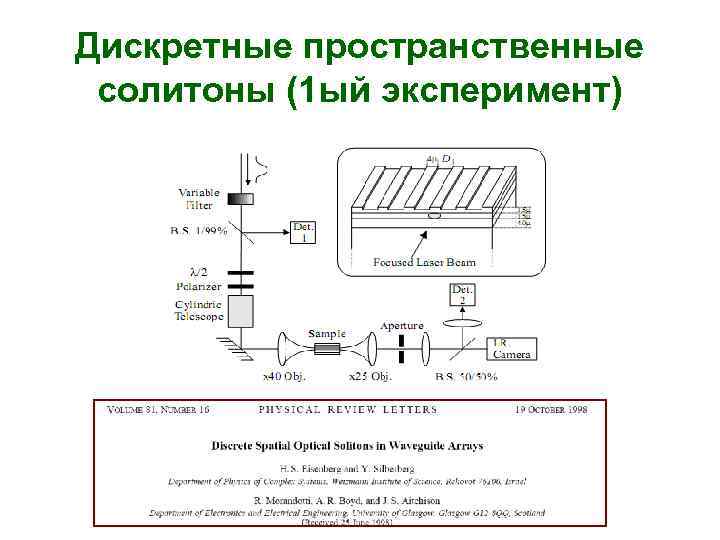Дискретные пространственные солитоны (Li. Nb. O 3: Ti: Fe)

Дискретные пространственные солитоны (Li. Nb. O 3: Ti: Fe)

2 D дискретные пространственные солитоны (SBN)

2 D дискретные пространственные солитоны (SBN)

2 D дискретные пространственные солитоны (SBN)

Спасибо за внимание!