Opt_sol_3_2.ppt
- Количество слайдов: 38
 Оптические солитоны (Лекция 3) В. М. Шандаров Томский государственный университет систем управления и радиоэлектроники
Оптические солитоны (Лекция 3) В. М. Шандаров Томский государственный университет систем управления и радиоэлектроники
 Распространение светового пучка в нелинейно – оптической среде В среде с кубичной нелинейностью на частоте падающей световой волны возникает составляющая Pnl, величина которой пропорциональна квадрату ампитуды поля. Cветовое поле с неоднородным распределением интенсивности наводит в такой среде оптические неоднородности, которые, в свою очередь, могут изменять пространственную структуру самого поля. Это эффект пространственного самовоздействия светового поля или пучка. Рассмотрим основные особенности такого самовоздействия и некоторые его результаты.
Распространение светового пучка в нелинейно – оптической среде В среде с кубичной нелинейностью на частоте падающей световой волны возникает составляющая Pnl, величина которой пропорциональна квадрату ампитуды поля. Cветовое поле с неоднородным распределением интенсивности наводит в такой среде оптические неоднородности, которые, в свою очередь, могут изменять пространственную структуру самого поля. Это эффект пространственного самовоздействия светового поля или пучка. Рассмотрим основные особенности такого самовоздействия и некоторые его результаты.
 Световой пучок в нелинейно – оптической среде Пусть световой пучок падает на границу нелинейно – оптической среды. Его поле имеет вид: Здесь x и z – поперечная и продольная координаты, размер пучка в направлении x значительно больше, чем l, а в направлении y его поле однородно.
Световой пучок в нелинейно – оптической среде Пусть световой пучок падает на границу нелинейно – оптической среды. Его поле имеет вид: Здесь x и z – поперечная и продольная координаты, размер пучка в направлении x значительно больше, чем l, а в направлении y его поле однородно.
 Световой пучок в нелинейно – оптической среде Используем параксиальное приближение, т. е. считаем, что амплитуда A(x, z) изменяется в направлении z намного медленнее, чем в направлении x. Уравнение, описывающее поведение пучка в нелинейной диэлектрической среде, получим, исходя из стандартной системы уравнений Максвелла:
Световой пучок в нелинейно – оптической среде Используем параксиальное приближение, т. е. считаем, что амплитуда A(x, z) изменяется в направлении z намного медленнее, чем в направлении x. Уравнение, описывающее поведение пучка в нелинейной диэлектрической среде, получим, исходя из стандартной системы уравнений Максвелла:
 Световой пучок в нелинейно – оптической среде
Световой пучок в нелинейно – оптической среде
 Световой пучок в нелинейно – оптической среде
Световой пучок в нелинейно – оптической среде
 Световой пучок в нелинейно – оптической среде С учетом выражений для производных получим: Но для параксиальных пучков поэтому Здесь мы ограничились скалярным приближением, считая световой пучок линейно поляризованным.
Световой пучок в нелинейно – оптической среде С учетом выражений для производных получим: Но для параксиальных пучков поэтому Здесь мы ограничились скалярным приближением, считая световой пучок линейно поляризованным.
 Световой пучок в нелинейно – оптической среде Рассматриваемая среда является нелинейной, ее диэлектрическая проницаемость может быть представлена в форме: тогда или
Световой пучок в нелинейно – оптической среде Рассматриваемая среда является нелинейной, ее диэлектрическая проницаемость может быть представлена в форме: тогда или
 Световой пучок в нелинейно – оптической среде Правую часть последнего уравнения запишем в форме: Но nl можно представить как nl= – l= . Т. к. =n 2, то: и В итоге
Световой пучок в нелинейно – оптической среде Правую часть последнего уравнения запишем в форме: Но nl можно представить как nl= – l= . Т. к. =n 2, то: и В итоге
 Световой пучок в нелинейно – оптической среде Это уравнение для амплитуды светового пучка, распространяющегося в нелинейно – оптической среде. В его правой части нелинейная добавка к показателю преломления среды nnl является функцией пространственных координат и зависит от локальной интенсивности светового поля. Рассмотрим различные механизмы оптической нелинейности, приводящие к изменениям показателя преломления среды на частоте распространяющегося в ней светового поля.
Световой пучок в нелинейно – оптической среде Это уравнение для амплитуды светового пучка, распространяющегося в нелинейно – оптической среде. В его правой части нелинейная добавка к показателю преломления среды nnl является функцией пространственных координат и зависит от локальной интенсивности светового поля. Рассмотрим различные механизмы оптической нелинейности, приводящие к изменениям показателя преломления среды на частоте распространяющегося в ней светового поля.
 Керровская оптическая нелинейность Керровская нелинейность обусловлена нелинейной связью наведенной поляризации в среде и напряженности электрического поля в световой волне. Это n на частоте падающей волны в среде с кубичной нелинейностью: n(2) – нелинейный показатель преломления. Для обычных материалов (газы, жидкости, стекла, кристаллы) он мал, изменения n, приводящие к пространственному самовоздействию, требуют интенсивности света в сотни МВт/см 2 и более. Данный механизм практически безынерционен.
Керровская оптическая нелинейность Керровская нелинейность обусловлена нелинейной связью наведенной поляризации в среде и напряженности электрического поля в световой волне. Это n на частоте падающей волны в среде с кубичной нелинейностью: n(2) – нелинейный показатель преломления. Для обычных материалов (газы, жидкости, стекла, кристаллы) он мал, изменения n, приводящие к пространственному самовоздействию, требуют интенсивности света в сотни МВт/см 2 и более. Данный механизм практически безынерционен.
 Керровская оптическая нелинейность Знак n(2) определяет знак нелинейности среды. При n(2)>0 среда называется самофокусирующей, при n(2)<0 самодефокусирующей. В первой возможны эффекты самофокусировки, во второй – самодефокусировки.
Керровская оптическая нелинейность Знак n(2) определяет знак нелинейности среды. При n(2)>0 среда называется самофокусирующей, при n(2)<0 самодефокусирующей. В первой возможны эффекты самофокусировки, во второй – самодефокусировки.
 Термооптическая нелинейность – изменение показателя преломления при изменении температуры среды, обусловленном поглощением света. Величина изменения показателя преломления в этом случае определяется соотношением: -температурный коэффициент показателя преломления, - T[I(x, z)] – локальное изменение температуры среды вследствие поглощения света.
Термооптическая нелинейность – изменение показателя преломления при изменении температуры среды, обусловленном поглощением света. Величина изменения показателя преломления в этом случае определяется соотношением: -температурный коэффициент показателя преломления, - T[I(x, z)] – локальное изменение температуры среды вследствие поглощения света.
 Фоторефрактивная птическая нелинейность Оптическая нелинейность, обусловленная фоторефрактивным эффектом. Она обусловлена изменением показателя преломления вследствие линейного электрооптического эффекта при условии индуцирования светом в фоторефрактивном кристалле электрического поля пространственного заряда. Она может быть поистине гигантской, приводя к значительным возмущениям показателя преломления даже при микроваттных интенсивностях света. Однако она также значительно медленнее в сравнении с керровской и во многих случаях медленнее термооптической.
Фоторефрактивная птическая нелинейность Оптическая нелинейность, обусловленная фоторефрактивным эффектом. Она обусловлена изменением показателя преломления вследствие линейного электрооптического эффекта при условии индуцирования светом в фоторефрактивном кристалле электрического поля пространственного заряда. Она может быть поистине гигантской, приводя к значительным возмущениям показателя преломления даже при микроваттных интенсивностях света. Однако она также значительно медленнее в сравнении с керровской и во многих случаях медленнее термооптической.
 Дрейфовый механизм Разделение носителей электрического заряда (электронов или дырок) под действием приложенного к кристаллу внешнего электрического поля. Свободные носители перемещаются из освещенных областей кристалла в неосвещенные, где захватываются глубокими ловушечными центрами.
Дрейфовый механизм Разделение носителей электрического заряда (электронов или дырок) под действием приложенного к кристаллу внешнего электрического поля. Свободные носители перемещаются из освещенных областей кристалла в неосвещенные, где захватываются глубокими ловушечными центрами.
 Дрейфовый механизм где Ibg – интенсивность фоновой подсветки; Eext – напряженность внешнего электрического поля, приложенного к кристаллу; B - постоянная, зависящая от физических характеристик и электрооптических коэффициентов материала.
Дрейфовый механизм где Ibg – интенсивность фоновой подсветки; Eext – напряженность внешнего электрического поля, приложенного к кристаллу; B - постоянная, зависящая от физических характеристик и электрооптических коэффициентов материала.
 Фотовольтаический механизм В некоторых кристаллах без центра симметрии, при их однородном освещении, вдоль полярной оси кристалла возникает стационарный ток, плотность которого пропорциональна интенсивности света. Изменения показателя преломления для фотовольтаического механизма фоторефракции определяются выражением: Id – так называемая темновая интенсивность
Фотовольтаический механизм В некоторых кристаллах без центра симметрии, при их однородном освещении, вдоль полярной оси кристалла возникает стационарный ток, плотность которого пропорциональна интенсивности света. Изменения показателя преломления для фотовольтаического механизма фоторефракции определяются выражением: Id – так называемая темновая интенсивность
 Диффузионный механизм Распределение концентрации фотовозбужденных носителей в пространстве является неоднородным при неоднородности интенсивности возбуждающего светового поля. Вследствие эффекта тепловой диффузии возникает диффузионный ток, локальная величина которого пропорциональна градиенту концентрации носителей в данной точке пространства. Диффузия приводит к переносу зарядов из освещенных областей в неосвещенные. Носители заряда захватываются ловушками, что приводит к возникновению наведенного поля пространственного заряда Esc.
Диффузионный механизм Распределение концентрации фотовозбужденных носителей в пространстве является неоднородным при неоднородности интенсивности возбуждающего светового поля. Вследствие эффекта тепловой диффузии возникает диффузионный ток, локальная величина которого пропорциональна градиенту концентрации носителей в данной точке пространства. Диффузия приводит к переносу зарядов из освещенных областей в неосвещенные. Носители заряда захватываются ловушками, что приводит к возникновению наведенного поля пространственного заряда Esc.
 Пространственные оптические солитоны Пространственный оптический солитон – режим распространения светового пучка с сохранением его поперечного профиля вследствие компенсации эффекта дифракции за счет эффекта пространственного самовоздействия. В этом случае решение уравнения ищем в виде
Пространственные оптические солитоны Пространственный оптический солитон – режим распространения светового пучка с сохранением его поперечного профиля вследствие компенсации эффекта дифракции за счет эффекта пространственного самовоздействия. В этом случае решение уравнения ищем в виде
 Пространственные оптические солитоны Производные:
Пространственные оптические солитоны Производные:
 Пространственные оптические солитоны Это уравнение для пространственных солитонов, которое называют нелинейным уравнением Шредингера (НУШ) Пространственный оптический солитон можно представить в виде направляемой моды нелинейного волновода, индуцированного в среде самим световым полем
Пространственные оптические солитоны Это уравнение для пространственных солитонов, которое называют нелинейным уравнением Шредингера (НУШ) Пространственный оптический солитон можно представить в виде направляемой моды нелинейного волновода, индуцированного в среде самим световым полем
 Пространственные оптические солитоны Нелинейная добавка к показателю преломления среды nnl может быть как положительной, так и отрицательной. Соответственно, нелинейная добавка положительна либо отрицательна. В первом случае ( nnl>0) среда является самофокусирующей, а решение НУШ представляет собой светлый солитон, т. е. световой пучок, распространяющийся без дифракционного расплывания в нелинейно – оптической среде. Противоположный случай соответствует самодефокусирующей среде. Собственное решение НУШ при этом называют темным солитоном, под которым понимается как бы бездифракционное поведение неосвещенной области в световом поле.
Пространственные оптические солитоны Нелинейная добавка к показателю преломления среды nnl может быть как положительной, так и отрицательной. Соответственно, нелинейная добавка положительна либо отрицательна. В первом случае ( nnl>0) среда является самофокусирующей, а решение НУШ представляет собой светлый солитон, т. е. световой пучок, распространяющийся без дифракционного расплывания в нелинейно – оптической среде. Противоположный случай соответствует самодефокусирующей среде. Собственное решение НУШ при этом называют темным солитоном, под которым понимается как бы бездифракционное поведение неосвещенной области в световом поле.
 Пространственные солитоны в керровской среде
Пространственные солитоны в керровской среде
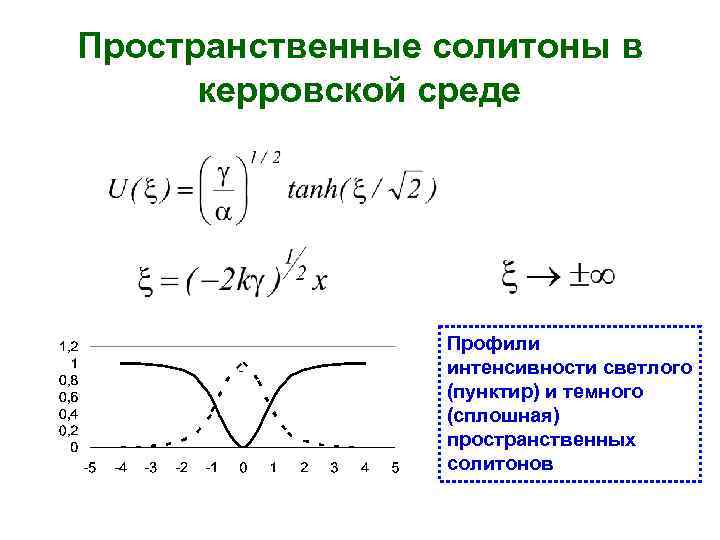 Пространственные солитоны в керровской среде Профили интенсивности светлого (пунктир) и темного (сплошная) пространственных солитонов
Пространственные солитоны в керровской среде Профили интенсивности светлого (пунктир) и темного (сплошная) пространственных солитонов
 Пространственные солитоны в фоторефрактивной среде В случае фотовольтаических солитонов:
Пространственные солитоны в фоторефрактивной среде В случае фотовольтаических солитонов:
 Пространственные солитоны в фоторефрактивной среде В случае дрейфового механизма:
Пространственные солитоны в фоторефрактивной среде В случае дрейфового механизма:
 Пространственные солитоны в фоторефрактивной среде Правая часть уравнений может быть как положительной, так и отрицательной. Это соответствует случаям самофокусирующей и самодефокусирующей нелинейностей. Для фотовольтаического эффекта знак нелинейности определяется направлением фотовольтаического тока. Для дрейфового механизма фоторефракции это соответствует прямой или обратной полярности приложенного к кристаллу внешнего электрического поля. В результате решения данных уравнений дают режимы светлых и темных пространственных солитонов.
Пространственные солитоны в фоторефрактивной среде Правая часть уравнений может быть как положительной, так и отрицательной. Это соответствует случаям самофокусирующей и самодефокусирующей нелинейностей. Для фотовольтаического эффекта знак нелинейности определяется направлением фотовольтаического тока. Для дрейфового механизма фоторефракции это соответствует прямой или обратной полярности приложенного к кристаллу внешнего электрического поля. В результате решения данных уравнений дают режимы светлых и темных пространственных солитонов.
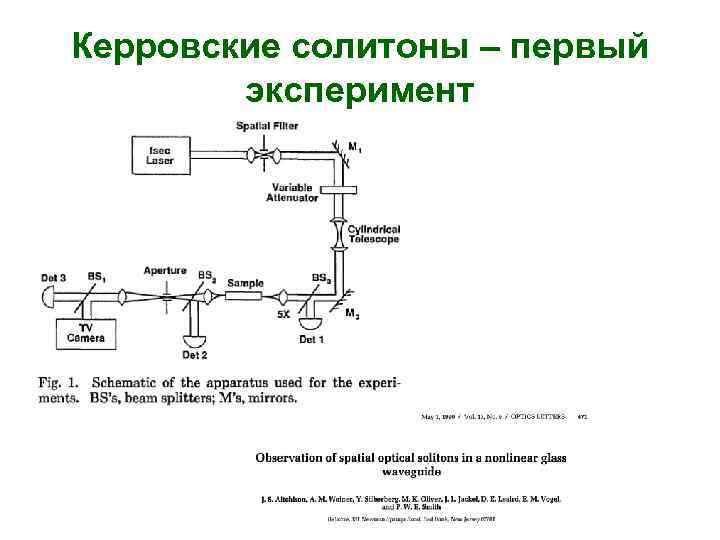 Керровские солитоны – первый эксперимент
Керровские солитоны – первый эксперимент
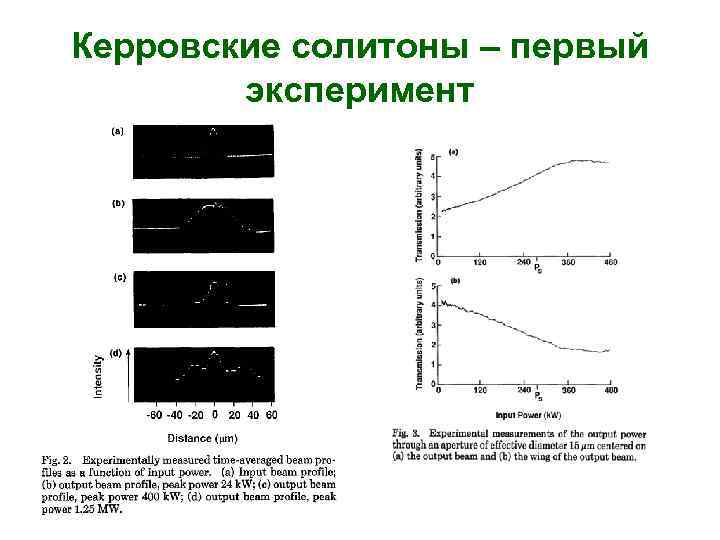 Керровские солитоны – первый эксперимент
Керровские солитоны – первый эксперимент
 Термооптические солитоны
Термооптические солитоны
 Термооптические солитоны
Термооптические солитоны
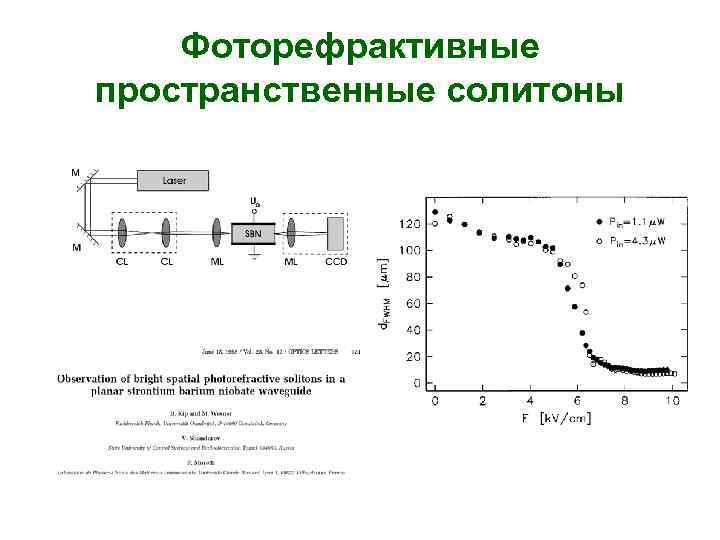 Фоторефрактивные пространственные солитоны
Фоторефрактивные пространственные солитоны
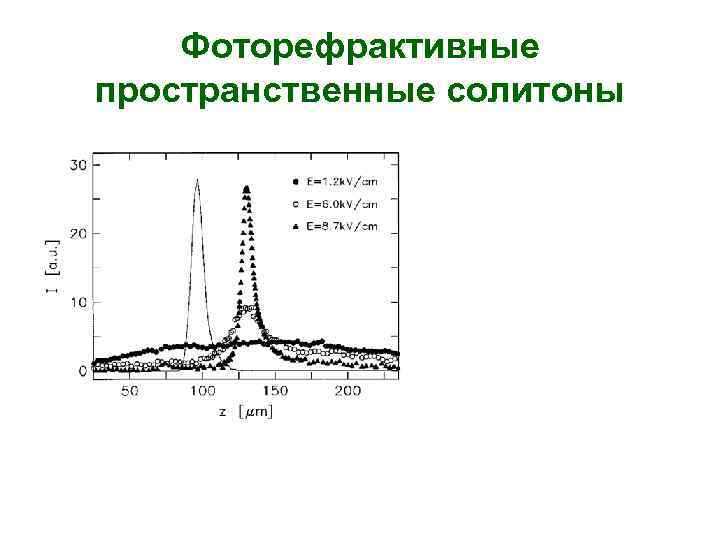 Фоторефрактивные пространственные солитоны
Фоторефрактивные пространственные солитоны
 Фоторефрактивные пространственные солитоны
Фоторефрактивные пространственные солитоны
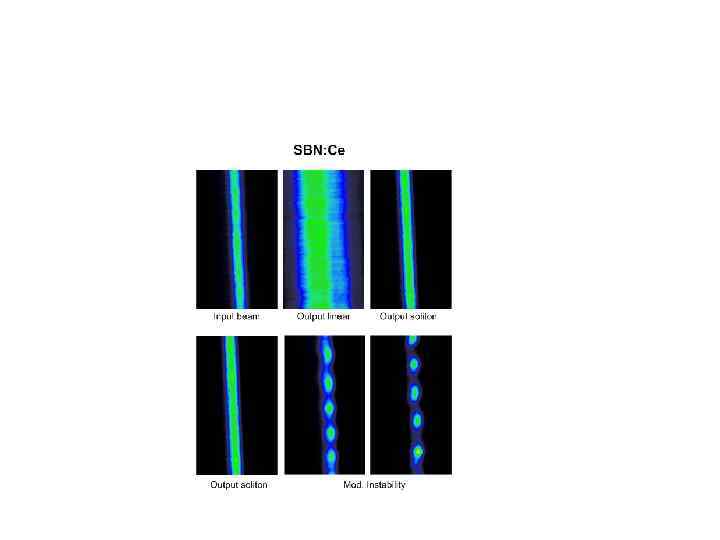
 Светлые солитоны в ниобате лития
Светлые солитоны в ниобате лития
 где А – константа, зависящая от физических характеристик и электрооптических коэффициентов материала; Id – так называемая темновая интенсивность, определяемая условием , т. е. интенсивность света, при которой величина фотопроводимости материала равна его темновой проводимости. Для дрейфового механизма: где Ibg – интенсивность фоновой подсветки; Eext – напряженность внешнего электрического поля, приложенного к кристаллу; B постоянная, зависящая от физических характеристик и электрооптических коэффициентов материала.
где А – константа, зависящая от физических характеристик и электрооптических коэффициентов материала; Id – так называемая темновая интенсивность, определяемая условием , т. е. интенсивность света, при которой величина фотопроводимости материала равна его темновой проводимости. Для дрейфового механизма: где Ibg – интенсивность фоновой подсветки; Eext – напряженность внешнего электрического поля, приложенного к кристаллу; B постоянная, зависящая от физических характеристик и электрооптических коэффициентов материала.
 Уравнение позволяет проследить, как изменяется профиль светового пучка в нелинейной среде при различных механизмах и величине оптической нелинейности, а также различных параметрах светового пучка. Особый интерес представляют решения уравнения, отвечающие режимам сохранения поперечного профиля светового пучка, называемым режимами пространственных оптических солитонов. В таком случае решение (8. 42) ищем в виде:
Уравнение позволяет проследить, как изменяется профиль светового пучка в нелинейной среде при различных механизмах и величине оптической нелинейности, а также различных параметрах светового пучка. Особый интерес представляют решения уравнения, отвечающие режимам сохранения поперечного профиля светового пучка, называемым режимами пространственных оптических солитонов. В таком случае решение (8. 42) ищем в виде:


