Определенный интеграл Лекция 13 Понятие интегральной

Определенный интеграл Лекция № 13

Понятие интегральной суммы Пусть функция f(x) задана на отрезке [a, b]. Разобьем отрезок [a, b] на n произвольных частей точками a = x 0 < x 1 < x 2 < … < xi+1 < … < xn = b. xi = xi – xi– 1 Точки xi – называются точками разбиения. Выберем на каждом из частичных отрезков [xi– 1, xi] произвольную точку i xi– 1 i xi , 0 i n. Составим интегральную сумму 2

3

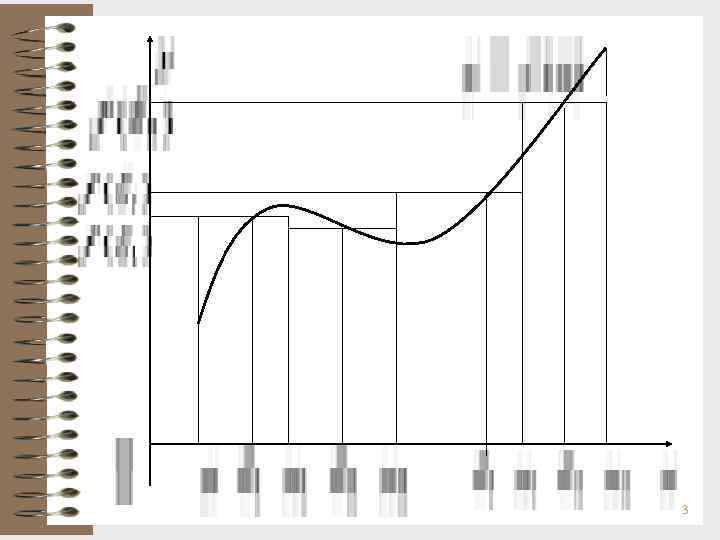
Геометрический смысл интегральной суммы i = f( i) xi – площадь под прямой y = f(xi) на отрезке [xi– 1, xi]. Вся интегральная сумма = 1 + 2 + … n – площадь под ломаной, образованной на каждом из отрезков [xi– 1, xi] прямой y = f( i), || оси Ох. 4

Понятие определенного интеграла Обозначим max xi максимальную из длин отрезков [xi– 1, xi]. Определение. Пусть предел интегральной суммы при max хi 0 существует, конечен и не зависит от способа выбора точек х1, х2, … и точек 1, 2, … Тогда этот предел называется определенным интегралом от функции y = f(x) на [a, b], обозначается Сама функция y = f(x) называется интегрируемой на отрезке [a, b], т. е. 5

Число a называется нижним пределом, b – верхним пределом, f(x) – подынтегральной функцией, f(x)dx - подынтегральным выражением. Задача о нахождении называется интегрированием функции f(x) на отрезке [a, b]. Не имеет значения, какой буквой обозначена переменная интегрирования: 6

Геометрический смысл определенного интеграла Пусть y = f(x) 0 на [a, b] (a < b). 7

Экономический смысл интеграла Пусть функция z = f(t) описывает изменение производительности некоторого производства с течением времени t. 8

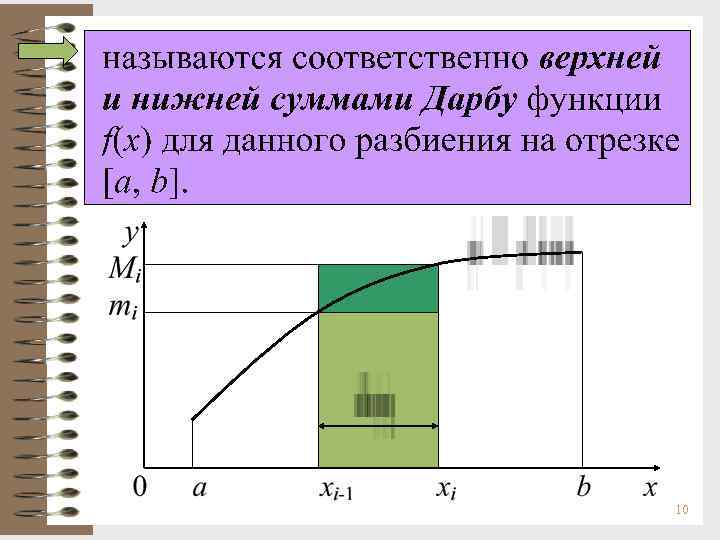
Суммы Дарбу Пусть f(x) ограничена на отрезке [a, b] и некоторое разбиение этого отрезка точками a=x 0 < x 1 < …< xn=b. Пусть mi и Mi соответственно точная нижняя и верхняя грани f(x) на частичном отрезке [xi-1, xi]. Тогда суммы 9

10

Очевидно s S. Необходимое и достаточное условие интегрируемости (Доказательство самостоятельно). 11

Классы интегрируемых функций (Доказательство самостоятельно). 12

Основные свойства определенного интеграла 1. По определению полагаем и Доказательство. Равенство верно, т. к. при движении от b к a все длины частичных отрезков xi < 0 в интегральной сумме. Ч. т. д. 13

2. Для любых чисел a, b и c имеет место равенство Доказательство. Положим a < c < b. Пусть с – одна из точек разбиения с = xm. Тогда интегральную сумму можно разбить на две суммы Переходя к пределу при max xi 0, получим равенство. Случай a < b < c доказывается аналогично. 14

3. Постоянный множитель можно выносить за знак определенного интеграла 4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их определенных интегралов 15

Свойства 3 и 4 доказываются единообразно исходя из интегральных сумм. Доказательство. По определению 16

Формулы оценки определенных интегралов Доказательство: Для любого разбиения отрезка [a, b] и при любом выборе точек i интегральная сумма при b>a. Переходя к пределу при max xi 0 получим свойство 1. Ч. т. д. 17

Доказательство. Это свойство следует из оценки 1) и свойства определенного интеграла 4) применительно к функции g(x) – f(x) 0. 18

Доказательство. 1. Покажем интегрируемость |f(x)|. 19

Предел правой части существует, следовательно сущетсвует предел и левой части. 2. 20

Доказательство. По условию m f(x) M для x [a, b]. Применяя оценку 2) и свойство 5) к неравенствам получим оценку интеграла. 21

Формулы среднего значения 22

Доказательство. Для функции f(x) выполняется оценка 4). Поделив обе части неравенства на b – a, имеем Обозначая утверждение теоремы. 23

В силу 2 -й теоремы Больцано-Коши о промежуточном значении такая точка с [a, b], что f(с) = , Это равенство называется формулой среднего значения, а величина f(с) – средним значением функции f(x) на отрезке [a, b]. 24

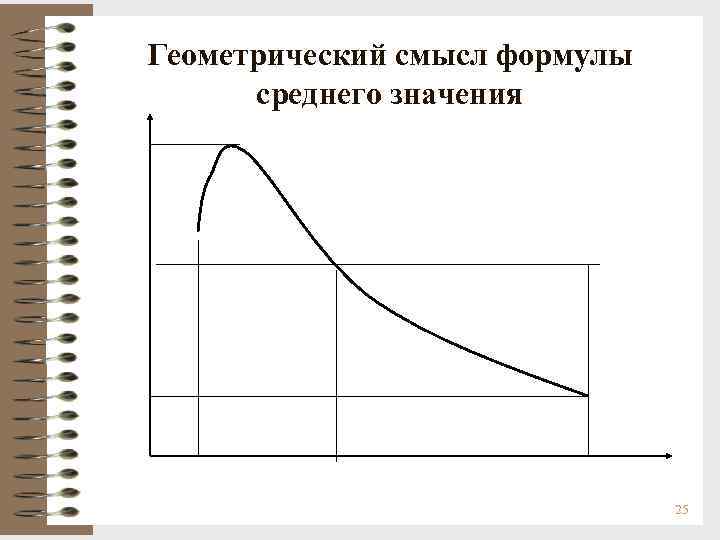Геометрический смысл формулы среднего значения 25

На основании оценки 1) и 2), а также свойства 3) можно доказать обобщенную теорему о среднем: 26

Определенный интеграл с переменным верхним пределом Если f(x) интегрируема на [a, b], то она интегрируема и на [a, x] , где x [a, b]. Рассмотрим функцию которую назовем интегралом с переменным верхним пределом. Теорема. Непрерывная на отрезке [a, b] функция f(x) имеет на этом отрезке первообразную. Одной из первообразных является функция 27

Доказательство. Возьмем x [a, b] и значение x+ x [a, b], x 0. Тогда Используем теорему о среднем 28

где с [x, x+ x]. При x 0 точка с х f(с) f(x). или F`(x) = f(x). Ч. т. д. 29

Формула Ньютона-Лейбница Доказательство. Учтем 30

(С – сonst). Подставляя х = а и учитывая свойство 1): Тогда при х=b получим Ч. т. д. 31

Равенство называется основной формулой интегрального исчисления или формулой Ньютона-Лейбница. 32

Разность F(b) – F(a) условно записывают символом , т. е. 33

Примеры. 34

Определенный интеграл 35

Теорема. Пусть Тогда справедлива формула 36

Доказательство. Пусть F(x) - первообразная f(x) на [a, b]. Рассмотрим сложную функцию Ф(t) = F[ (t)]. По правилу дифференцирования сложной функции Ф`(t) = F `[ (t)] `(t) = f [ (t)] `(t). По формуле Ньютона-Лейбница Ч. т. д. 37

Доказанная формула называется формулой замены переменной или подстановки в определенном интеграле. Замечание. При вычислении определенного интеграла с помощью замены переменной не обязательно возвращаться к прежней переменной. При подстановке следует сначала найти новые пределы интегрирования и выполнить необходимые преобразования подынтегральной функции. 38

Примеры. Применим подстановку x=a sint. dx=a cost dt. Заменим пределы интегрирования Найдем новые пределы: 39

Интегрирование по частям в определенном интеграле 40

Доказательство. Учтем справедливость доказываемой формулы. 41

Примеры. 42