ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 1 1 Задача приводящая к

ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 1

1. Задача, приводящая к понятию определенного интеграла. Определение Вычислить площадь криволинейной трапеции, нижним основанием которой является отрезок [a; b] оси ОХ, боковые стороны параллельны оси ОУ, а верхним основанием является кривая y=f(x) , причем и непрерывна на интервале. (рис. 1). Разобьем отрезок [a; b] произвольным образом на n частей точками 2

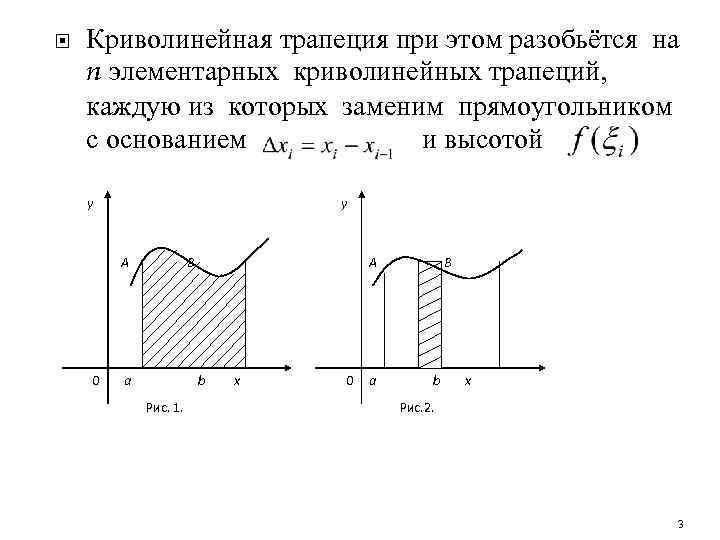Криволинейная трапеция при этом разобьётся на n элементарных криволинейных трапеций, каждую из которых заменим прямоугольником с основанием и высотой y y А 0 А В a b Рис. 1. x 0 a В b x Рис. 2. 3

где - произвольная точка из отрезка Площадь каждого прямоугольника равна: Сумма площадей прямоугольников , называемая интегральной суммой функции на интервале [a; b], приближенно равна площади криволинейной трапеции. Увеличивая число n разбиений отрезка [a; b] на элементарные интервалы так, что длина наибольшего из них , будем получать значения , которые все более приближаются к площади криволинейной. 4

трапеции. Перейдем к пределу при , , тем самым . Если этот предел существует и конечен, то говорят, что функция f(x) интегрируема на интервале [a; b] и называют определённым интегралом. Геометрически: площадь криволинейной трапеции. Теорема существования и единственности. 5

2. Свойства определенного интеграла 1. Определённый интеграл не зависит от переменной интегрирования: 2. Постоянный множитель можно выносить за знак определённого интеграла: 6

3. Интеграл от суммы конечного числа функций равен сумме интегралов от функций слагаемых: 4. Если верхний и нижний пределы интегрирования совпадают, то интеграл равен нулю: 5. Если пределы интегрирования поменять местами, то интеграл поменяет знак на противоположный: 7

6. Для любых a, b, c справедливо равенство (свойство аддитивности): 7. Если для всех неравенство (a < b) выполняется , то 8. Если m и M – наименьшее и наибольшее значения f(x) на интервале [a; b] , 8

то: 9. Теорема о среднем значении: если f(x) непрерывна на [a; b] , то внутри этого интервала существует такая точка c (a < c < b) , что 9

3. Формула Ньютона-Лейбница Для вычисления определенного интеграла используется формула Ньютона-Лейбница: где F(x) - первообразная для функции f(x). 10

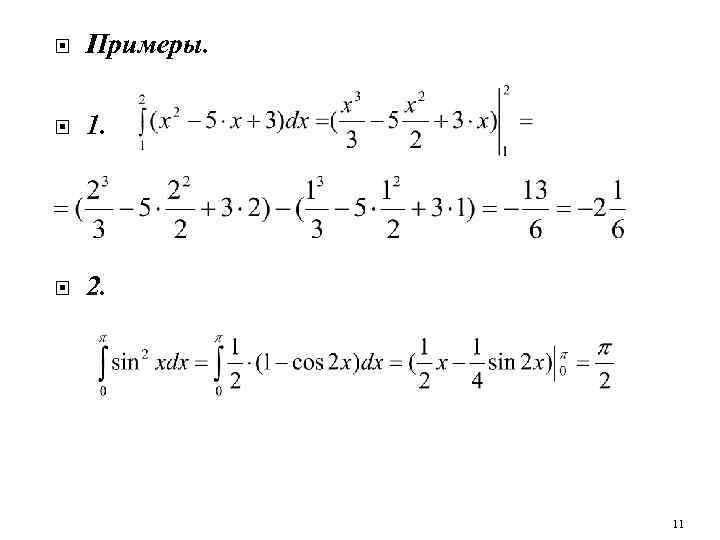Примеры. 1. 2. 11

Интегрирование по частям в определённом интеграле. Если функции u(x) и v(x) непрерывны и дифференцируемы на отрезке [a; b], то Или 12

Примеры. 1. 2. 13

Замена переменной в определённом интеграле. При вычислении определённых интегралов часто бывает удобно заменить переменную подобно тому, как этот приём использовался при нахождении неопределённых интегралов. Если функция f(x) непрерывна на отрезке [a, b] и функция, непрерывная вместе со своей производной на отрезке , где причем определена и непрерывна на отрезке , 14

то Примеры. Используя замену переменной, вычислить интегралы. 1. Примем. Тогда При этом, если x=1, то t=1; если то. , 15

Выполнив замену переменной, получим: 2. Положим Тогда при , ; при 16

Получим: Замечание: При интегрировании чётных и нечётных функций на симметричном отрезке [ a; a] справедливы следующие равенства: 17

для нечётной функции f(x) для чётной функции f(x) Примеры: 18

Геометрические приложения определенных интегралов. Вычисление площадей плоских фигур. Площадь в прямоугольных координатах. Если непрерывная кривая задана в прямоугольных координатах уравнением y=f(x), причём , то площадь криволинейной трапеции, ограниченной этой кривой, двумя вертикалями в точках х=а и х=в и отрезком оси абсцисс , определяется формулой. 19

В более общем случае, если площадь S ограничена двумя непрерывными кривыми и и двумя вертикалями х=а и х=в, y А В S 0 a b x Рис. 3. 20

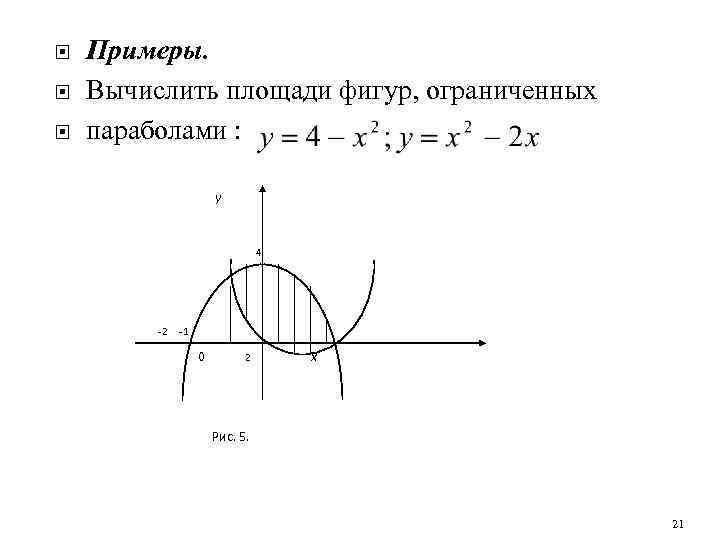Примеры. Вычислить площади фигур, ограниченных параболами : y 4 -2 -1 0 2 x Рис. 5. 21

Решив совместно уравнения находим абсциссы точек пересечения парабол: , которые будут являться пределами интегрирования (рис. 5). Искомая площадь равна: 22

Несобственные интегралы Под несобственными интегралами понимают интегралы с бесконечными пределами интегрирования или интегралы от неограниченных функций. 1. Несобственные интегралы с бесконечными пределами ( I рода ). Пусть функция f(x) определена и непрерывна при всех. Несобственный интеграл от f(x) в пределах от a до + ∞ определяется равенством 23

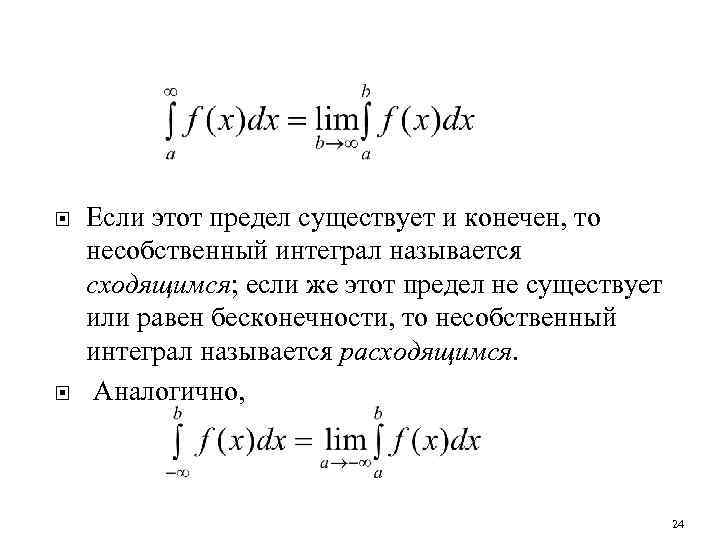Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же этот предел не существует или равен бесконечности, то несобственный интеграл называется расходящимся. Аналогично, 24

и Примеры. Вычислить несобственные интегралы или установить их расходимость. Решение. 25

Так как предел косинуса на бесконечности не существует, то данный несобственный интеграл расходится. то есть несобственный интеграл сходится и равен 1/32 26

Третий интеграл зависит от значения p. При p=1 данный интеграл примет вид: то есть несобственный интеграл расходится. Если p ≠ 1, то интеграл примет вид : Полученный предел зависит от значения p. 27

Если p > 1, то несобственный интеграл сходится. Если p < 1, то несобственный интеграл расходится. 28

Вывод: несобственный интеграл сходится при p > 1 и расходится при p ≤ 1. 2. Несобственные интегралы от неограниченных функций ( II рода). Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a; b] и непрерывна при a ≤ x < c и c < x ≤ b, то 29

по определению полагают: Несобственный интеграл ( где f(c)→ ∞, a < c < b ) называется сходящимся, если существуют оба предела в правой части равенства, и расходящимися, если не существует хотя бы один из них. 30

Примеры. Вычислить несобственные интегралы или установить их расходимость. 1. 1. Подынтегральная функция x=0 терпит разрыв, поэтому 2. в точке 31

Так как полученные пределы бесконечны, то данный несобственный интеграл расходится. 2) Подынтегральная функция в точке x=2 неогр. , следовательно несобственный интеграл сходится и равен 4. 32