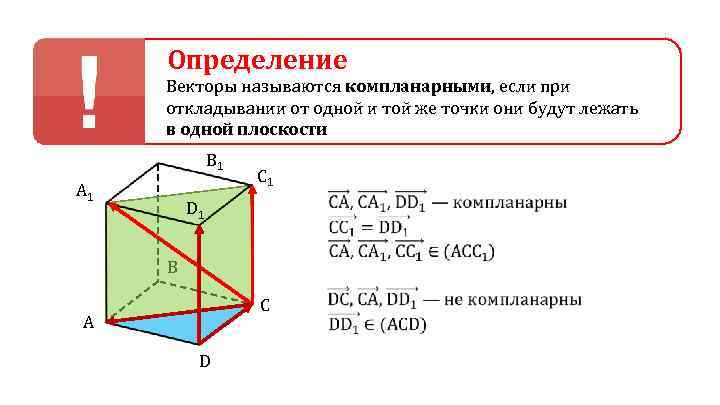
Скачать презентацию Определение Векторы называются компланарными если при откладывании от
40. Компланарные вектора.ppt
- Количество слайдов: 7
Определение Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать в одной плоскости B 1 A 1 C 1 D 1 B C A D
— Любые два вектора компланарны — Три вектора, среди которых имеются два коллинеарных, также компланарны — Три произвольных вектора могут быть как компланарными, так и некомпланарными
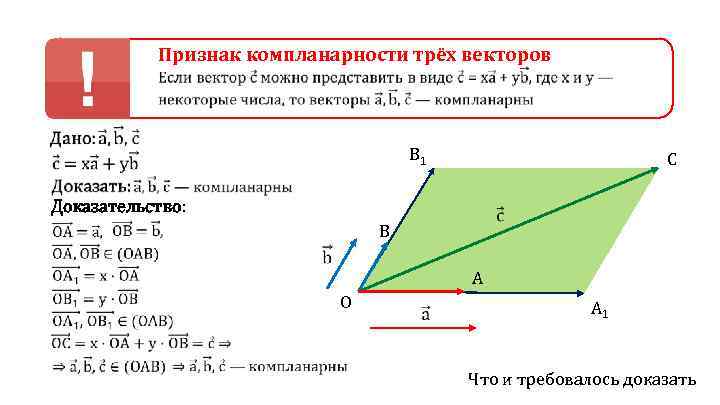Признак компланарности трёх векторов Доказательство: B 1 C B A O A 1 Что и требовалось доказать
Утверждение, обратное признаку компланарности векторов:
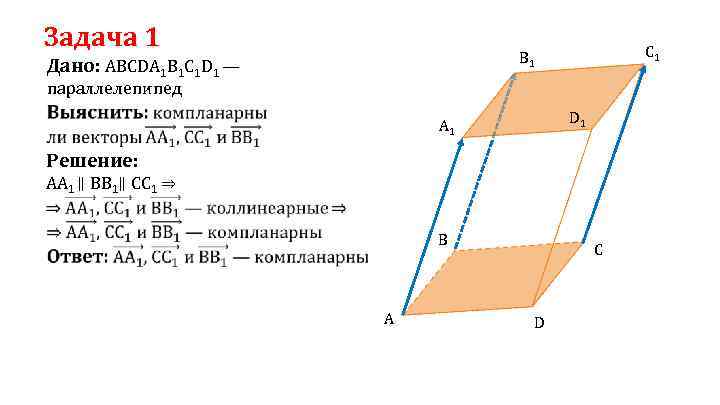Задача 1 C 1 B 1 Дано: ABCDA 1 B 1 C 1 D 1 — параллелепипед D 1 A 1 Решение: АА 1 ∥ BB 1∥ CC 1 ⇒ B A C D
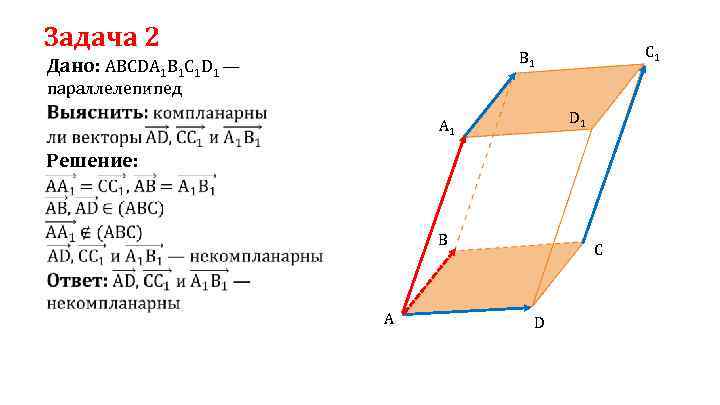Задача 2 C 1 B 1 Дано: ABCDA 1 B 1 C 1 D 1 — параллелепипед D 1 A 1 Решение: B A C D