Определение синуса косинуса и тангенса угла Цели

Определение синуса, косинуса и тангенса угла.

Цели и задачи: Знать определения синуса, косинуса и тангенса угла. Уметь находить значения синуса, косинуса и тангенса по таблицам В. М. Брадиса, с помощью единичной окружности. Уметь решать уравнения: sinx=0; sinx=1; sinx=-1; cosx=0; cosx=1; cosx=-1.

Повторение y М 1) α > 0 стрелки Путь = α α 0 Р (1; 0) x α М 2) α < 0 3) α = 0 Р→М против часовой Р- остается на месте Р→М по часовой стрелке Путь = │ α │

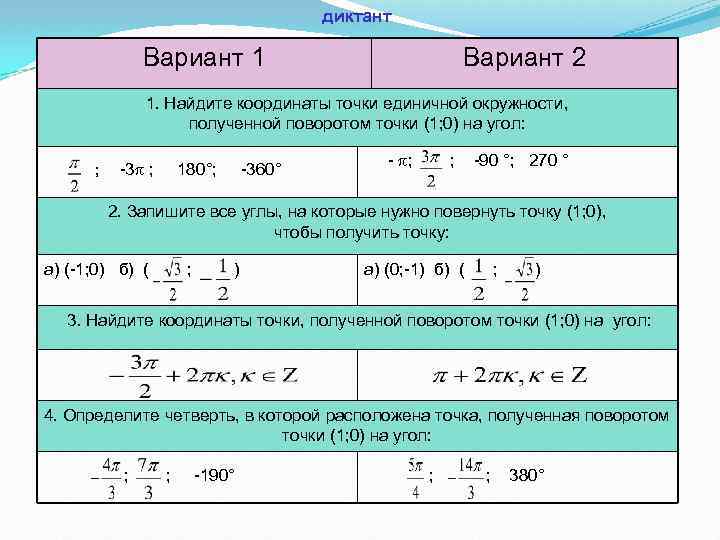диктант Вариант 1 Вариант 2 1. Найдите координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол: ; -3 ; 180°; -360° - ; ; -90 °; 270 ° 2. Запишите все углы, на которые нужно повернуть точку (1; 0), чтобы получить точку: а) (-1; 0) б) ( ; ) а) (0; -1) б) ( ; ) 3. Найдите координаты точки, полученной поворотом точки (1; 0) на угол: 4. Определите четверть, в которой расположена точка, полученная поворотом точки (1; 0) на угол: ; ; -190° ; ; 380°

Ответы к диктанту (взаимопроверка) Вариант 1 1. (0; 1); (-1; 0); (1; 0) Вариант 2 1. (-1; 0); (0; -1); (0; -1) 9 -10 – « 5» 2. а) 5 – 6 – « 3» б) 3. 4. 7 - 8 – « 4» б) (0; 1) II, 0 – 4 – « 2» 3. II (-1; 0) 4. III, I

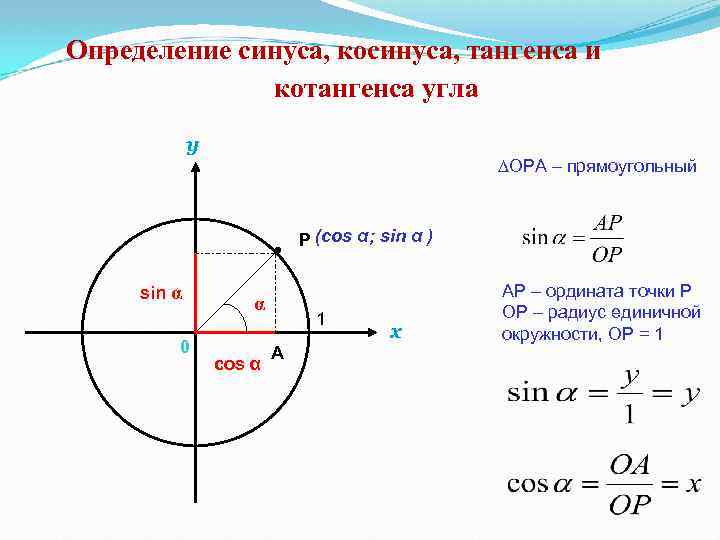Определение синуса, косинуса, тангенса и котангенса угла y ∆ОРА – прямоугольный P (cos α; sin α ) sin α 0 α cos α 1 A x АР – ордината точки Р ОР – радиус единичной окружности, ОР = 1

Синусом угла α называется ордината точки, полученной поворотом точки Р (1; 0) вокруг начала координат на угол α. Косинусом – абсцисса этой точки Тангенсом угла α называется отношение синуса угла α к его косинусу. Котангенс угла α – это отношение косинуса угла α к его синусу.

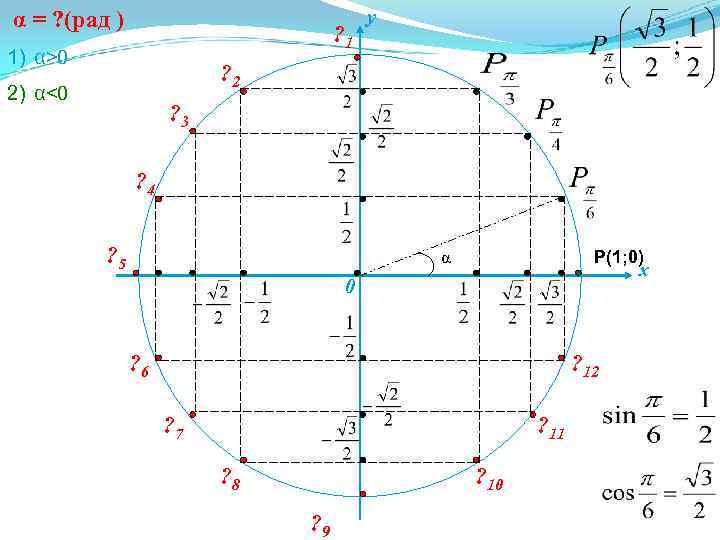α = ? (рад ) ? 1 1) α>0 y ? 2 2) α<0 ? 3 ? 4 ? 5 Р(1; 0) α x 0 ? 6 ? 12 ? 7 ? 11 ? 8 ? 10 ? 9

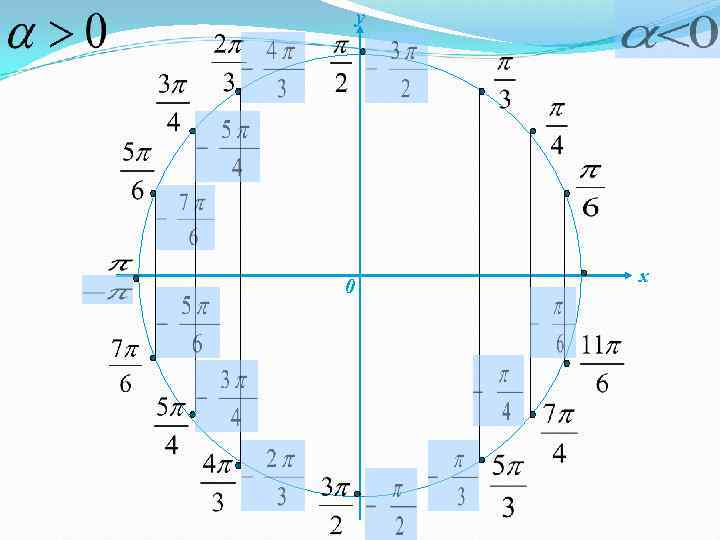y 0 x

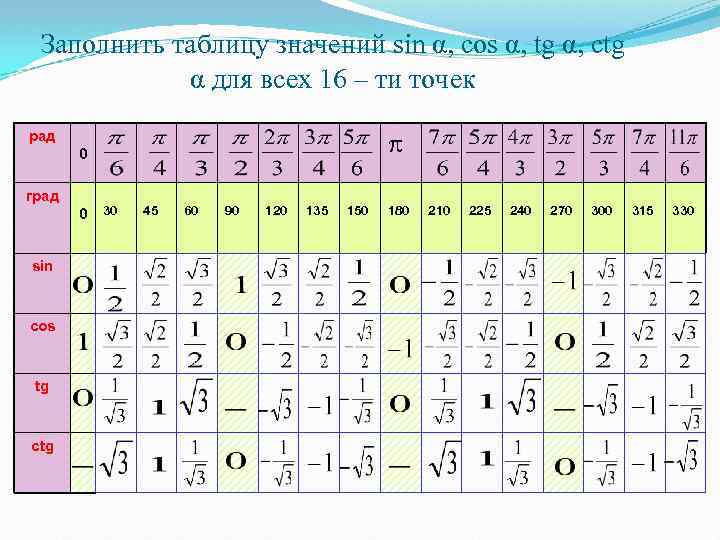Заполнить таблицу значений sin α, cos α, tg α, ctg α для всех 16 – ти точек рад 0 град 0 sin cos tg ctg 30 45 60 90 120 135 150 180 210 225 240 270 300 315 330

Решим уравнение: sin x = 0 Нужно найти все углы, синус которых равен нулю. Ординату, равную нулю, имеют две точки единичной окружности: (1; 0) и (-1; 0) y Эти точки получаются 2 (-1; 0) (1; 0) 0 - поворотом точки (1; 0) на углы 0, , 2 , 3 и т. д. , а так же на углы - , -2 , -3 и т. д. x Следовательно, sin x = 0 при x= k, где k – любое целое число. Ответ.

Решить уравнения: cos x = 0, cos x =1, sin x =1 cos x = 0 cos x =1 sin x =1

Закрепление изученного материала Устно. Вычислить с помощью таблицы. =0 =1 =-1 =-1 =1