комбинации тел.ppt
- Количество слайдов: 22
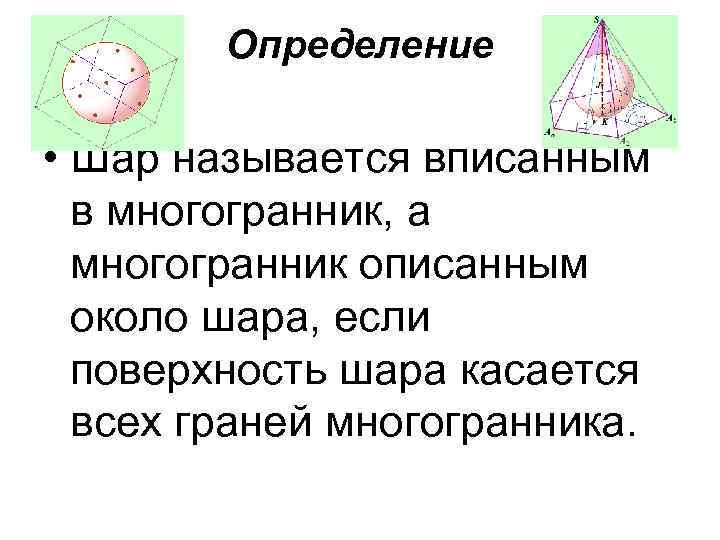 Определение • Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.
Определение • Шар называется вписанным в многогранник, а многогранник описанным около шара, если поверхность шара касается всех граней многогранника.
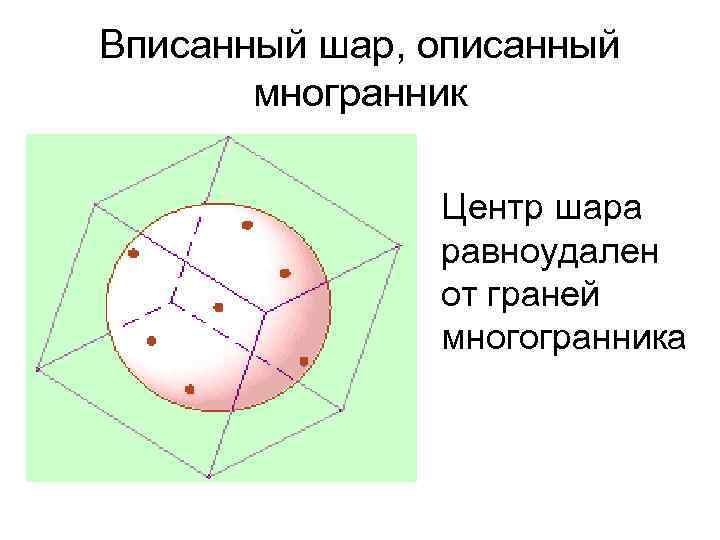 Вписанный шар, описанный многранник Центр шара равноудален от граней многогранника
Вписанный шар, описанный многранник Центр шара равноудален от граней многогранника
 Вопросы • 1. Можно ли в параллелепипед с размерами 3, 3, 5 вписать шар? • Можно ли в четырехугольную правильную призму со стороной основания 2 и боковым ребром 2 вписать шар? • Можно ли в шестиугольную правильную призму со стороной основания 4 и боковым ребром 8 вписать шар?
Вопросы • 1. Можно ли в параллелепипед с размерами 3, 3, 5 вписать шар? • Можно ли в четырехугольную правильную призму со стороной основания 2 и боковым ребром 2 вписать шар? • Можно ли в шестиугольную правильную призму со стороной основания 4 и боковым ребром 8 вписать шар?
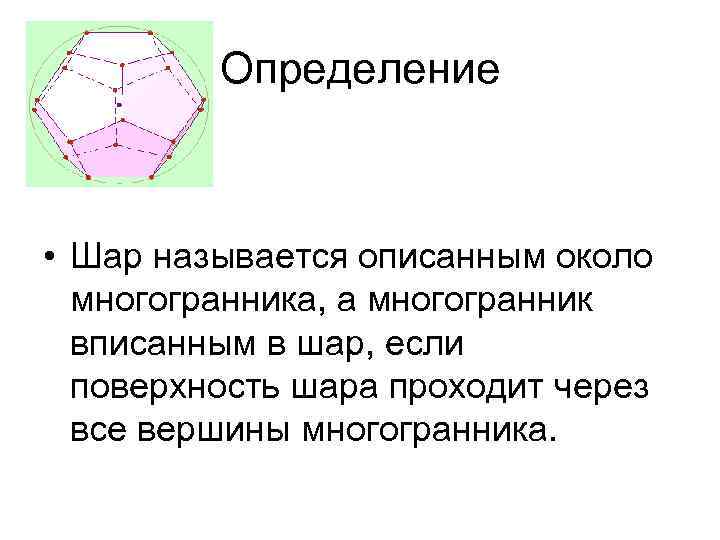 Определение • Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника.
Определение • Шар называется описанным около многогранника, а многогранник вписанным в шар, если поверхность шара проходит через все вершины многогранника.
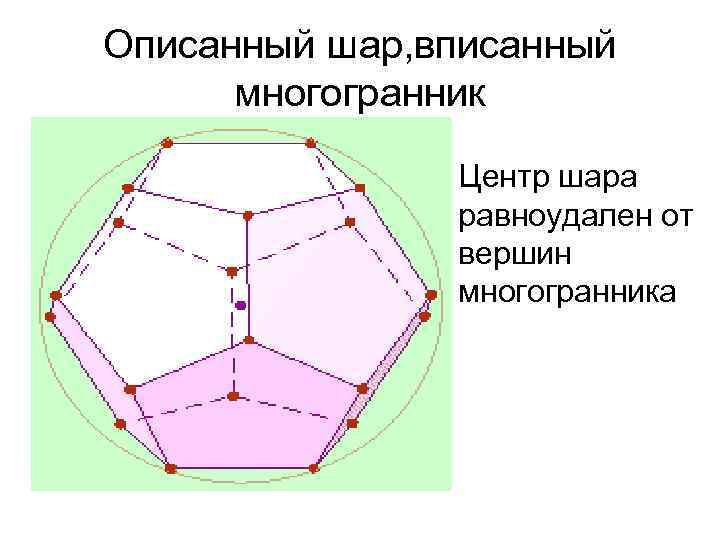 Описанный шар, вписанный многогранник Центр шара равноудален от вершин многогранника
Описанный шар, вписанный многогранник Центр шара равноудален от вершин многогранника
 Вопросы • 1. Можно ли около параллелепипеда с размерами 3, 4, 5 описать шар? • Можно ли около четырехугольной правильной призмы со стороной основания 2 и боковым ребром 2 описать шар? • Можно ли около шестиугольной правильной призмы со стороной основания 4 и боковым ребром 8 описать шар?
Вопросы • 1. Можно ли около параллелепипеда с размерами 3, 4, 5 описать шар? • Можно ли около четырехугольной правильной призмы со стороной основания 2 и боковым ребром 2 описать шар? • Можно ли около шестиугольной правильной призмы со стороной основания 4 и боковым ребром 8 описать шар?
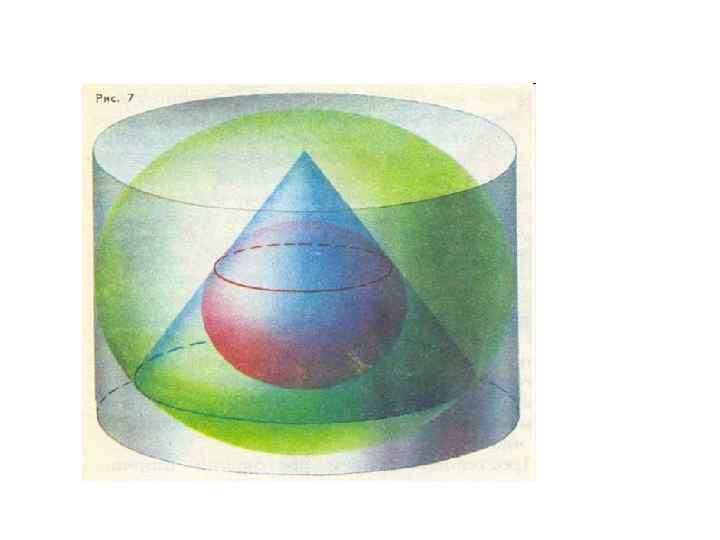
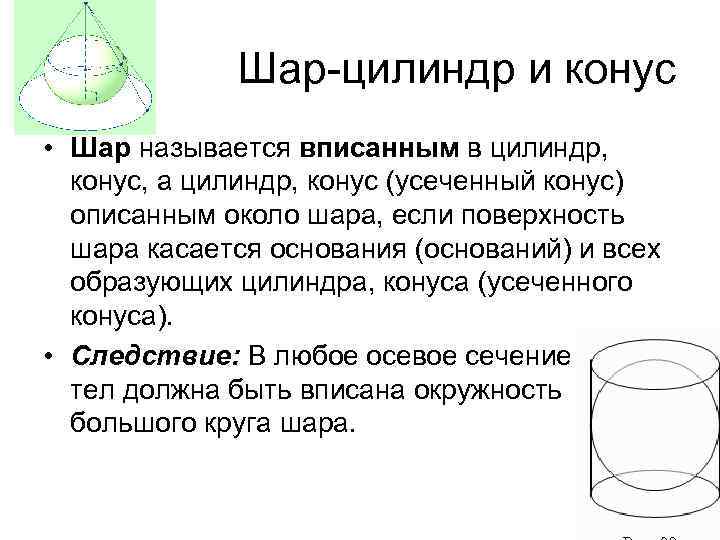 Шар-цилиндр и конус • Шар называется вписанным в цилиндр, конус, а цилиндр, конус (усеченный конус) описанным около шара, если поверхность шара касается основания (оснований) и всех образующих цилиндра, конуса (усеченного конуса). • Следствие: В любое осевое сечение этих тел должна быть вписана окружность большого круга шара.
Шар-цилиндр и конус • Шар называется вписанным в цилиндр, конус, а цилиндр, конус (усеченный конус) описанным около шара, если поверхность шара касается основания (оснований) и всех образующих цилиндра, конуса (усеченного конуса). • Следствие: В любое осевое сечение этих тел должна быть вписана окружность большого круга шара.
 Вопросы • Верно ли, что в любой конус можно вписать шар? • Верно ли, что в любой цилиндр можно вписать шар? • В какой цилиндр можно вписать шар?
Вопросы • Верно ли, что в любой конус можно вписать шар? • Верно ли, что в любой цилиндр можно вписать шар? • В какой цилиндр можно вписать шар?
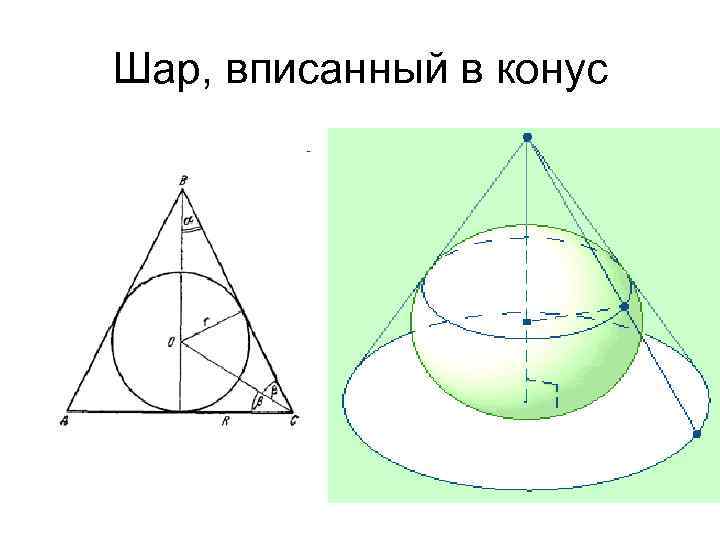 Шар, вписанный в конус
Шар, вписанный в конус
 Комбинация шара с конусом • теорема • Около прямого кругового конуса можно описать шар. • В прямой круговой конус можно вписать шар • Центр шара находится на оси конуса.
Комбинация шара с конусом • теорема • Около прямого кругового конуса можно описать шар. • В прямой круговой конус можно вписать шар • Центр шара находится на оси конуса.
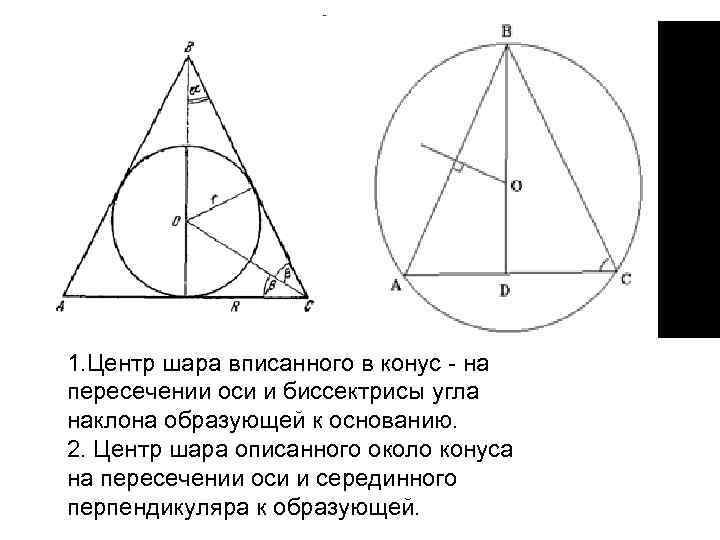 1. Центр шара вписанного в конус - на пересечении оси и биссектрисы угла наклона образующей к основанию. 2. Центр шара описанного около конуса на пересечении оси и серединного перпендикуляра к образующей.
1. Центр шара вписанного в конус - на пересечении оси и биссектрисы угла наклона образующей к основанию. 2. Центр шара описанного около конуса на пересечении оси и серединного перпендикуляра к образующей.
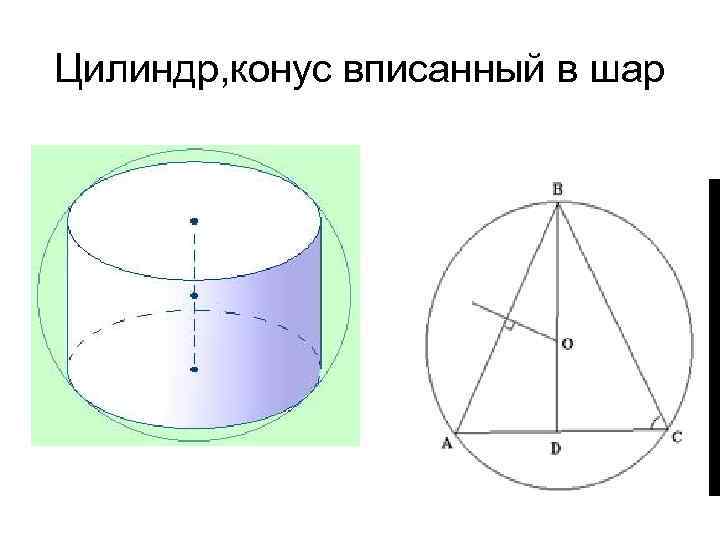 Цилиндр, конус вписанный в шар
Цилиндр, конус вписанный в шар
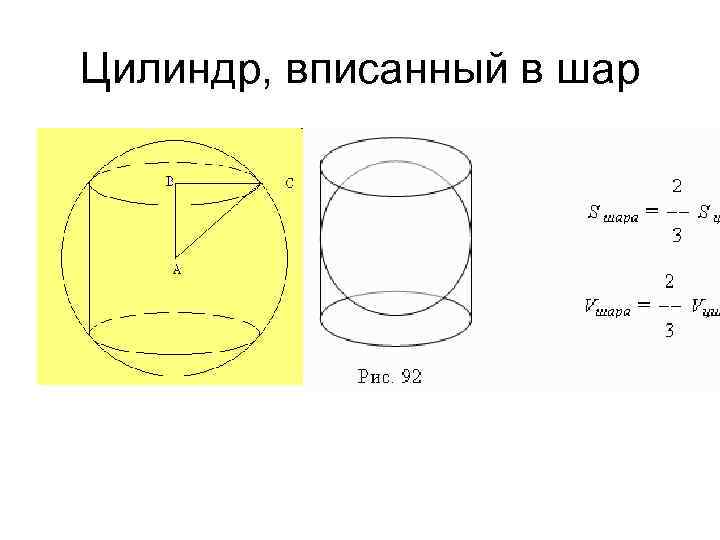 Цилиндр, вписанный в шар
Цилиндр, вписанный в шар
 Комбинация шара с цилиндром Теорема • Около прямого кругового цилиндра можно описать шар. • В прямой круговой цилиндр можно вписать шар в том и только том случае, если высота цилиндра равна его диаметру.
Комбинация шара с цилиндром Теорема • Около прямого кругового цилиндра можно описать шар. • В прямой круговой цилиндр можно вписать шар в том и только том случае, если высота цилиндра равна его диаметру.
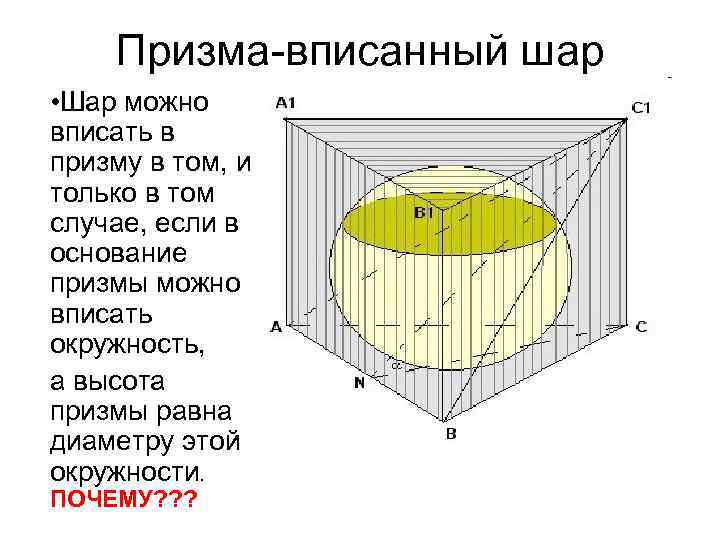 Призма-вписанный шар • Шар можно вписать в призму в том, и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. ПОЧЕМУ? ? ?
Призма-вписанный шар • Шар можно вписать в призму в том, и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. ПОЧЕМУ? ? ?
 Комбинация шара с призмой • 1. Шар, вписанный в прямую призму. • Шар можно вписать в призму в том, и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. • Центр шара находится на середине перпендикуляра, опущенного из центра вписанной в основание окружности
Комбинация шара с призмой • 1. Шар, вписанный в прямую призму. • Шар можно вписать в призму в том, и только в том случае, если в основание призмы можно вписать окружность, а высота призмы равна диаметру этой окружности. • Центр шара находится на середине перпендикуляра, опущенного из центра вписанной в основание окружности
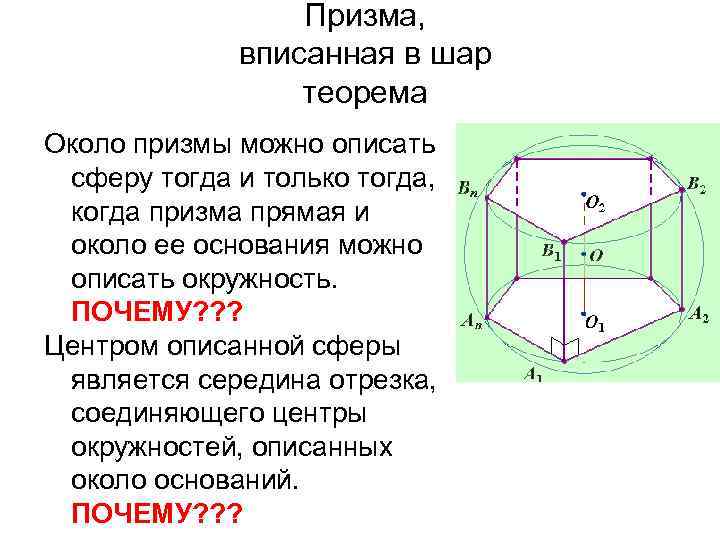 Призма, вписанная в шар теорема Около призмы можно описать сферу тогда и только тогда, когда призма прямая и около ее основания можно описать окружность. ПОЧЕМУ? ? ? Центром описанной сферы является середина отрезка, соединяющего центры окружностей, описанных около оснований. ПОЧЕМУ? ? ?
Призма, вписанная в шар теорема Около призмы можно описать сферу тогда и только тогда, когда призма прямая и около ее основания можно описать окружность. ПОЧЕМУ? ? ? Центром описанной сферы является середина отрезка, соединяющего центры окружностей, описанных около оснований. ПОЧЕМУ? ? ?
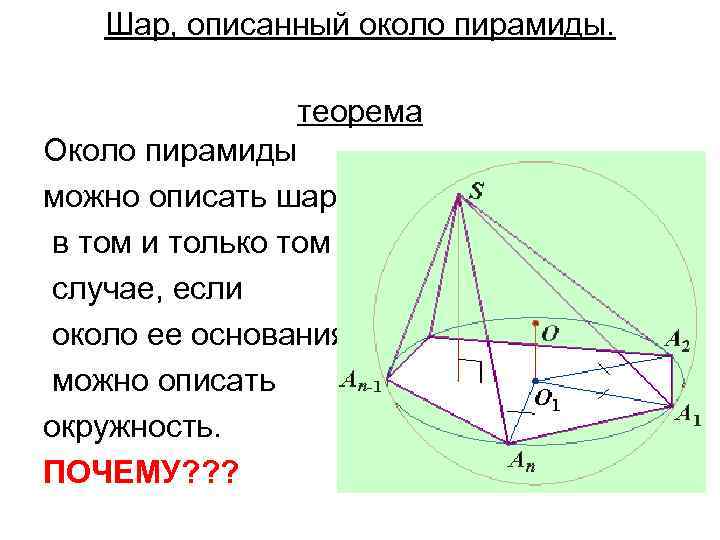 Шар, описанный около пирамиды. теорема Около пирамиды можно описать шар в том и только том случае, если около ее основания можно описать окружность. ПОЧЕМУ? ? ?
Шар, описанный около пирамиды. теорема Около пирамиды можно описать шар в том и только том случае, если около ее основания можно описать окружность. ПОЧЕМУ? ? ?
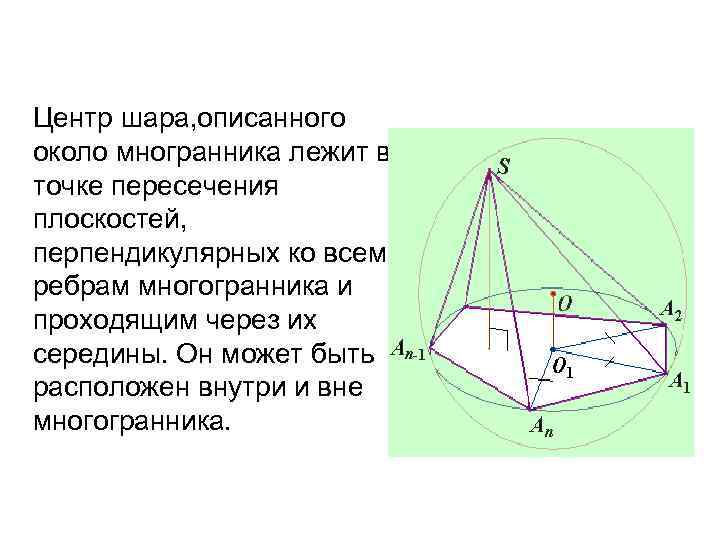 Центр шара, описанного около многранника лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящим через их середины. Он может быть расположен внутри и вне многогранника.
Центр шара, описанного около многранника лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящим через их середины. Он может быть расположен внутри и вне многогранника.
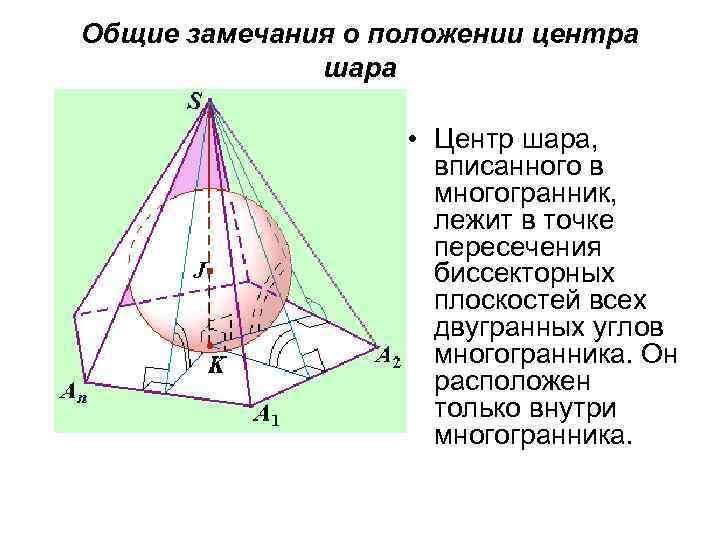 Общие замечания о положении центра шара • Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
Общие замечания о положении центра шара • Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.
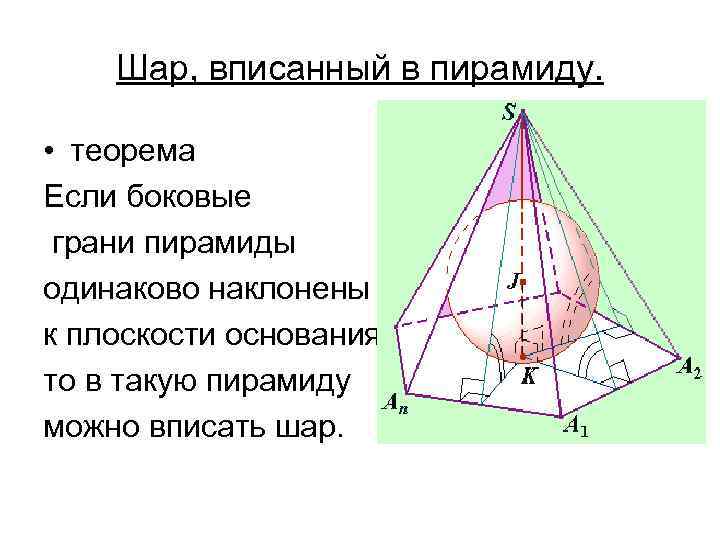 Шар, вписанный в пирамиду. • теорема Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать шар.
Шар, вписанный в пирамиду. • теорема Если боковые грани пирамиды одинаково наклонены к плоскости основания, то в такую пирамиду можно вписать шар.