Определение рекурсии 19









 Определение рекурсии 19 Задачи для домашнего решения 1. Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n. Составить программу определяющую количество цифр в числе с использованием рекурсии. 2. Разработать программу для нахождения наибольшего общего делителя (НОД) двух заданных натуральных чисел используя алгоритм Евклида
Определение рекурсии 19 Задачи для домашнего решения 1. Определим функцию K(n), которая возвращает количество цифр в заданном натуральном числе n. Составить программу определяющую количество цифр в числе с использованием рекурсии. 2. Разработать программу для нахождения наибольшего общего делителя (НОД) двух заданных натуральных чисел используя алгоритм Евклида
 Фракталы 20 Математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом в 1975 году был введен термин “фрактал” (от латинского fractus – раздробленный, разбитый, состоящий из фрагментов), а в 1982 году опубликована основополагающая книга “Фрактальная геометрия природы”, где описаны фрактальные множества, их свойства, методы получения и изображения.
Фракталы 20 Математиком Исследовательского центра корпорации IBM Бенуа Мандельбротом в 1975 году был введен термин “фрактал” (от латинского fractus – раздробленный, разбитый, состоящий из фрагментов), а в 1982 году опубликована основополагающая книга “Фрактальная геометрия природы”, где описаны фрактальные множества, их свойства, методы получения и изображения.
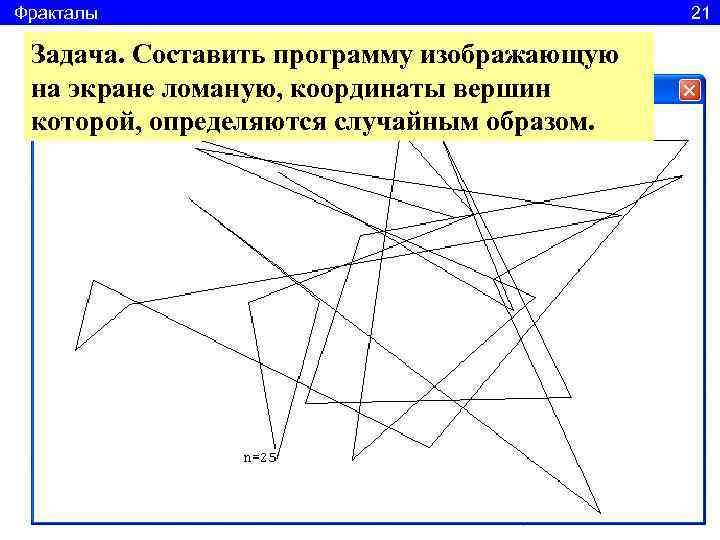
 Фракталы 21 Задача. Составить программу изображающую на экране ломаную, координаты вершин которой, определяются случайным образом.
Фракталы 21 Задача. Составить программу изображающую на экране ломаную, координаты вершин которой, определяются случайным образом.
 Фракталы 22 uses crt, graphabc; var x, y, x 2, y 2, i: integer; Координаты Цикл задающий begin начала первой количество линии clrscr; Координаты конца x : = random(640); звеньев Координаты y : = random(400); линии становятся конца линии for i: =1 to 25 do beginкоординатами Линия начала следующей x 2 : = random(640); линии y 2 : = random(400); line(x, y, x 2, y 2); x: =x 2; y: =y 2; end; textout(200, 330, 'n=25'); end.
Фракталы 22 uses crt, graphabc; var x, y, x 2, y 2, i: integer; Координаты Цикл задающий begin начала первой количество линии clrscr; Координаты конца x : = random(640); звеньев Координаты y : = random(400); линии становятся конца линии for i: =1 to 25 do beginкоординатами Линия начала следующей x 2 : = random(640); линии y 2 : = random(400); line(x, y, x 2, y 2); x: =x 2; y: =y 2; end; textout(200, 330, 'n=25'); end.
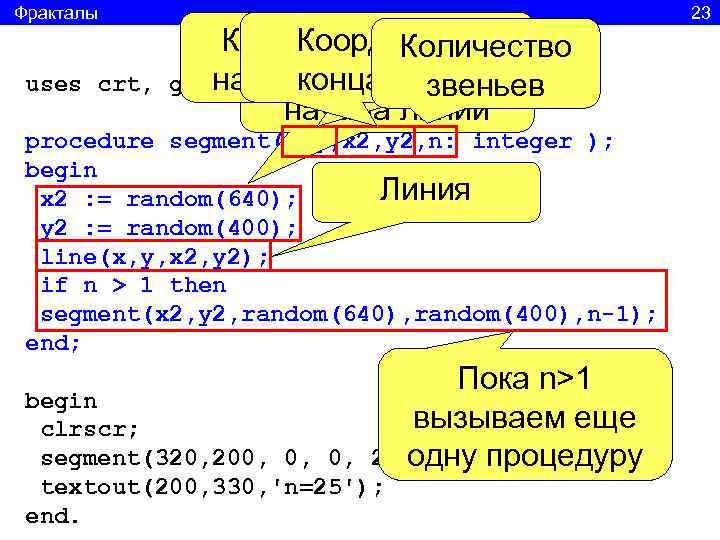
 Фракталы 23 Координаты. Количество Координаты uses crt, graphabc; Координаты начала звеньев конца звена начала линии procedure segment(x, y, x 2, y 2, n: integer ); begin x 2 : = random(640); Линия y 2 : = random(400); line(x, y, x 2, y 2); if n > 1 then segment(x 2, y 2, random(640), random(400), n-1); end; Пока n>1 begin clrscr; вызываем еще segment(320, 200, 0, 0, одну процедуру 25); textout(200, 330, 'n=25'); end.
Фракталы 23 Координаты. Количество Координаты uses crt, graphabc; Координаты начала звеньев конца звена начала линии procedure segment(x, y, x 2, y 2, n: integer ); begin x 2 : = random(640); Линия y 2 : = random(400); line(x, y, x 2, y 2); if n > 1 then segment(x 2, y 2, random(640), random(400), n-1); end; Пока n>1 begin clrscr; вызываем еще segment(320, 200, 0, 0, одну процедуру 25); textout(200, 330, 'n=25'); end.
 Фракталы 24 Задача. Составить программу изображающую на экране спираль.
Фракталы 24 Задача. Составить программу изображающую на экране спираль.
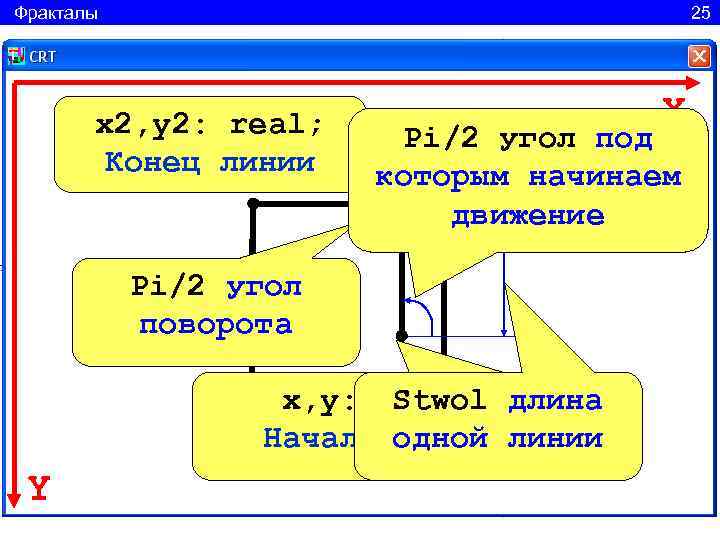
 Фракталы 25 x 2, y 2: real; X Pi/2 угол под Конец линии которым начинаем движение Pi/2 угол поворота x, y: real; длина Stwol Начало одной линии линии Y
Фракталы 25 x 2, y 2: real; X Pi/2 угол под Конец линии которым начинаем движение Pi/2 угол поворота x, y: real; длина Stwol Начало одной линии линии Y
 Фракталы 26 uses crt, graphabc; Пока n>1 Вычисляем procedure scroll(x, y, A, Stwol: real; n: integer ); var вызываем x 2, y 2: real; координаты конца процедуру рисования begin Рисуем линиюлинии x 2 : = x + Stwol * cos(A); линии каждой Для y 2 : = y - Stwol * sin(A); следующей линии line(round(x), round(y), round(x 2), round(y 2)); if n > 1 then поворачиваем на 90 scroll( x 2, y 2, A+Pi/2, Stwol+5, n-1); end; градусов begin clrscr; Каждую новую линию удлиняем на 5 scroll(300, 200, Pi/2, 10, 50); textout(200, 330, 'n=50'); end. единиц
Фракталы 26 uses crt, graphabc; Пока n>1 Вычисляем procedure scroll(x, y, A, Stwol: real; n: integer ); var вызываем x 2, y 2: real; координаты конца процедуру рисования begin Рисуем линиюлинии x 2 : = x + Stwol * cos(A); линии каждой Для y 2 : = y - Stwol * sin(A); следующей линии line(round(x), round(y), round(x 2), round(y 2)); if n > 1 then поворачиваем на 90 scroll( x 2, y 2, A+Pi/2, Stwol+5, n-1); end; градусов begin clrscr; Каждую новую линию удлиняем на 5 scroll(300, 200, Pi/2, 10, 50); textout(200, 330, 'n=50'); end. единиц
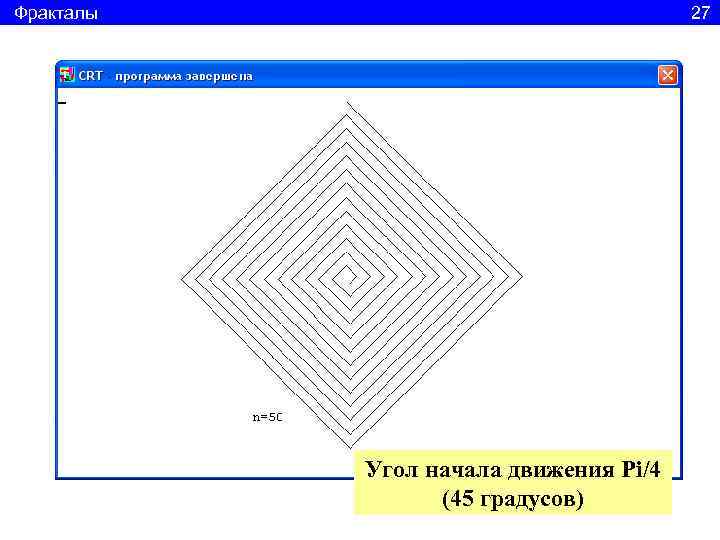
 Фракталы 27 Угол начала движения Pi/4 (45 градусов)
Фракталы 27 Угол начала движения Pi/4 (45 градусов)
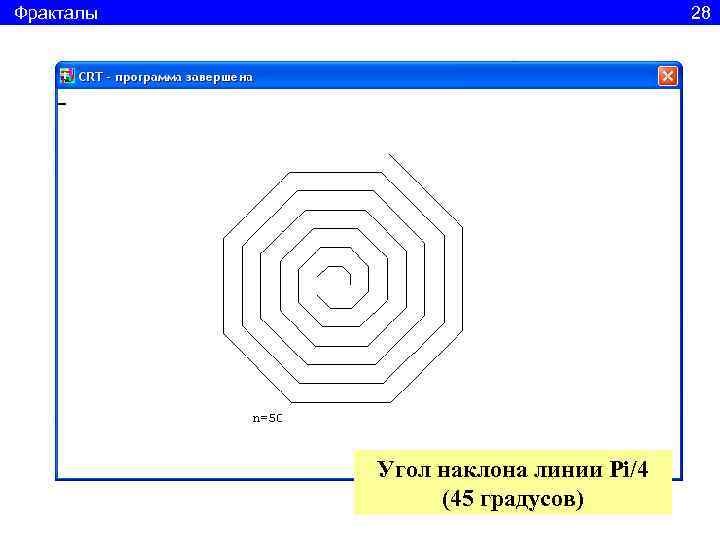
 Фракталы 28 Угол наклона линии Pi/4 (45 градусов)
Фракталы 28 Угол наклона линии Pi/4 (45 градусов)
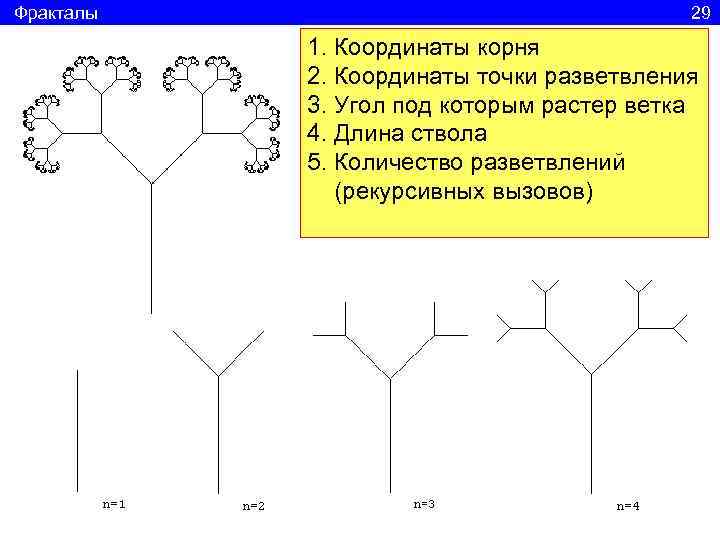
 Фракталы 29 1. Координаты корня 2. Координаты точки разветвления 3. Угол под которым растер ветка 4. Длина ствола 5. Количество разветвлений (рекурсивных вызовов)
Фракталы 29 1. Координаты корня 2. Координаты точки разветвления 3. Угол под которым растер ветка 4. Длина ствола 5. Количество разветвлений (рекурсивных вызовов)
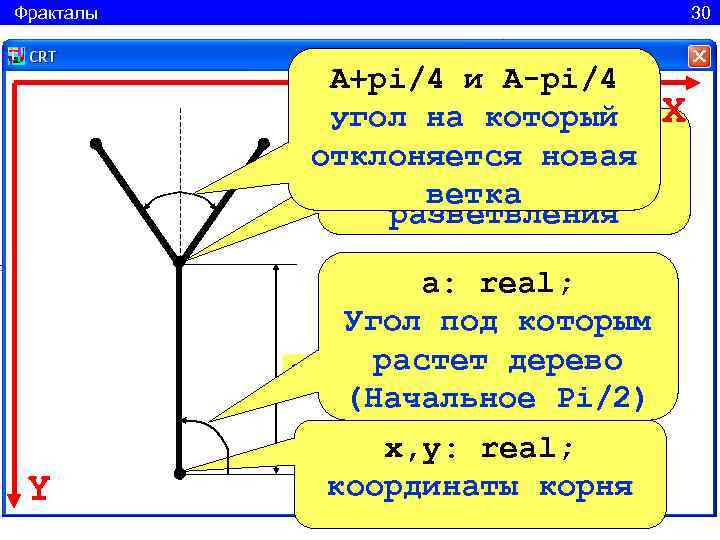
 Фракталы 30 A+pi/4 и A-pi/4 угол на который X x 2, y 2: real; отклоняется новая координаты точки ветка разветвления а: real; Угол под которым Stwol: растет длина ствола real; дерево (Начальное Pi/2) x, y: real; Y координаты корня
Фракталы 30 A+pi/4 и A-pi/4 угол на который X x 2, y 2: real; отклоняется новая координаты точки ветка разветвления а: real; Угол под которым Stwol: растет длина ствола real; дерево (Начальное Pi/2) x, y: real; Y координаты корня
 Фракталы 31 Координаты procedure Tree(x, y, A, Stwol: real; n: раза Пока n>1 два integer ); var точки вызываем процедуру x 2, y 2: real; разветвления begin для правой иодну ветвь Рисуем левой ветки x 2 : = x + Stwol * cos(A); y 2 : = y - Stwol * sin(A); line(round(x), round(y), round(x 2), round(y 2)); if n > 1 then begin Tree( x 2, y 2, A+Pi/4, 0. 6*Stwol, n-1); Tree( x 2, y 2, A-Pi/4, 0. 6*Stwol, n-1); end;
Фракталы 31 Координаты procedure Tree(x, y, A, Stwol: real; n: раза Пока n>1 два integer ); var точки вызываем процедуру x 2, y 2: real; разветвления begin для правой иодну ветвь Рисуем левой ветки x 2 : = x + Stwol * cos(A); y 2 : = y - Stwol * sin(A); line(round(x), round(y), round(x 2), round(y 2)); if n > 1 then begin Tree( x 2, y 2, A+Pi/4, 0. 6*Stwol, n-1); Tree( x 2, y 2, A-Pi/4, 0. 6*Stwol, n-1); end;
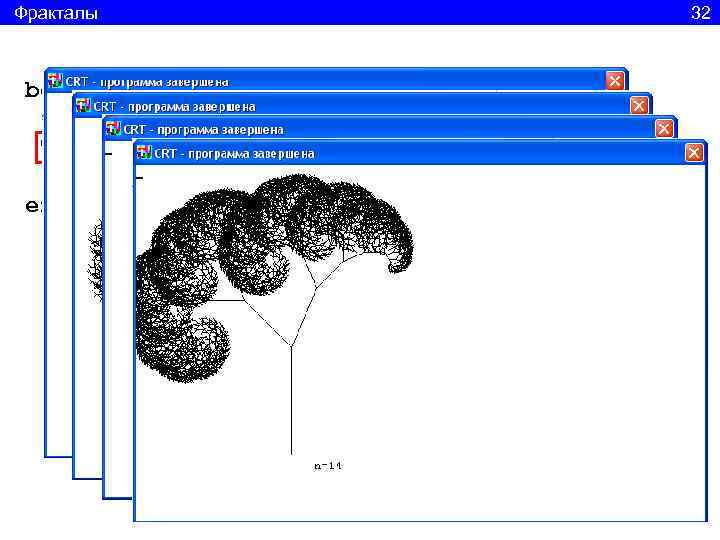
 Фракталы 32 begin clrscr; Tree(175, 325, Pi/2, 120, 14); textout(200, 330, 'n=14'); end. Вызов рекурсивной процедуры из тела программы
Фракталы 32 begin clrscr; Tree(175, 325, Pi/2, 120, 14); textout(200, 330, 'n=14'); end. Вызов рекурсивной процедуры из тела программы
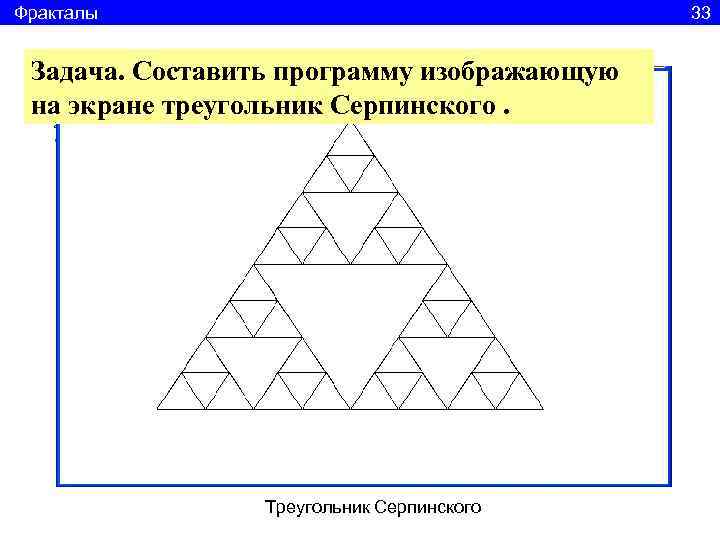
 Фракталы 33 Задача. Составить программу изображающую на экране треугольник Серпинского. Треугольник Серпинского
Фракталы 33 Задача. Составить программу изображающую на экране треугольник Серпинского. Треугольник Серпинского
 Фракталы 34 (x 2, y 2) X li ) n y 2 x 2, y 2 e( 2, x 3 xa, ya x (xb, yb) , y (xa, ya) y, xb, yb 3, x, x 2 ( ne , y li 2) x, y x 3, y 3 xa, ya xb, yb Y xc, yc (x, y) (xc, yc) line(x, y, x 3, y 3) (x 3, y 3)
Фракталы 34 (x 2, y 2) X li ) n y 2 x 2, y 2 e( 2, x 3 xa, ya x (xb, yb) , y (xa, ya) y, xb, yb 3, x, x 2 ( ne , y li 2) x, y x 3, y 3 xa, ya xb, yb Y xc, yc (x, y) (xc, yc) line(x, y, x 3, y 3) (x 3, y 3)
 Фракталы 35 procedure rec(x, y, x 2, y 2, x 3, y 3, n: integer); var xa, ya, xb, yb, xc, yc: integer; begin if n >0 then Рисуем треугол begin line(x, y, x 2, y 2); Вычисляем line(x 3, y 3, x 2, y 2); координаты серед line(x, y, x 3, y 3); Рекурсивно ри сторон треугольни xa: =(x+x 2) div 2; ya: =(y+y 2) div 2; меньших треу xb: =(x 3+x 2) div 2; yb: =(y 3+y 2) div 2; xc: =(x+x 3) div 2; yc: =(y+y 3) div 2; rec(x, y, xa, ya, xc, yc, n-1); rec(x 2, y 2, xa, ya, xb, yb, n-1); rec(x 3, y 3, xb, yb, xc, yc, n-1); end;
Фракталы 35 procedure rec(x, y, x 2, y 2, x 3, y 3, n: integer); var xa, ya, xb, yb, xc, yc: integer; begin if n >0 then Рисуем треугол begin line(x, y, x 2, y 2); Вычисляем line(x 3, y 3, x 2, y 2); координаты серед line(x, y, x 3, y 3); Рекурсивно ри сторон треугольни xa: =(x+x 2) div 2; ya: =(y+y 2) div 2; меньших треу xb: =(x 3+x 2) div 2; yb: =(y 3+y 2) div 2; xc: =(x+x 3) div 2; yc: =(y+y 3) div 2; rec(x, y, xa, ya, xc, yc, n-1); rec(x 2, y 2, xa, ya, xb, yb, n-1); rec(x 3, y 3, xb, yb, xc, yc, n-1); end;
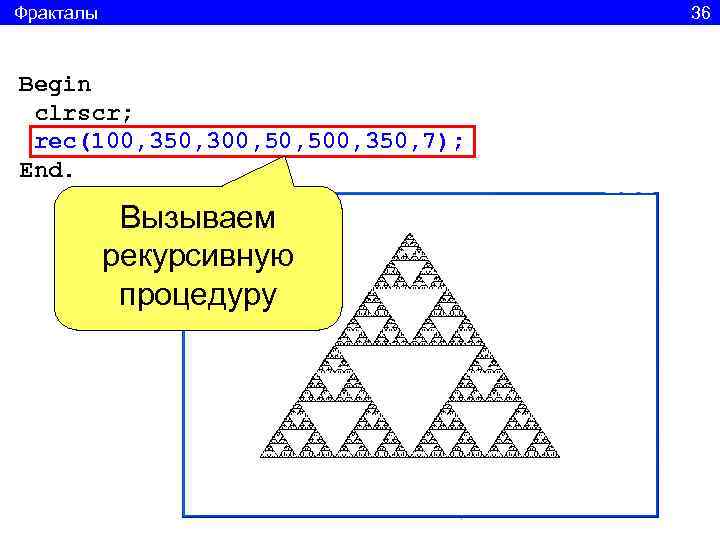
 Фракталы 36 Begin clrscr; rec(100, 350, 300, 500, 350, 7); End. Вызываем рекурсивную процедуру
Фракталы 36 Begin clrscr; rec(100, 350, 300, 500, 350, 7); End. Вызываем рекурсивную процедуру
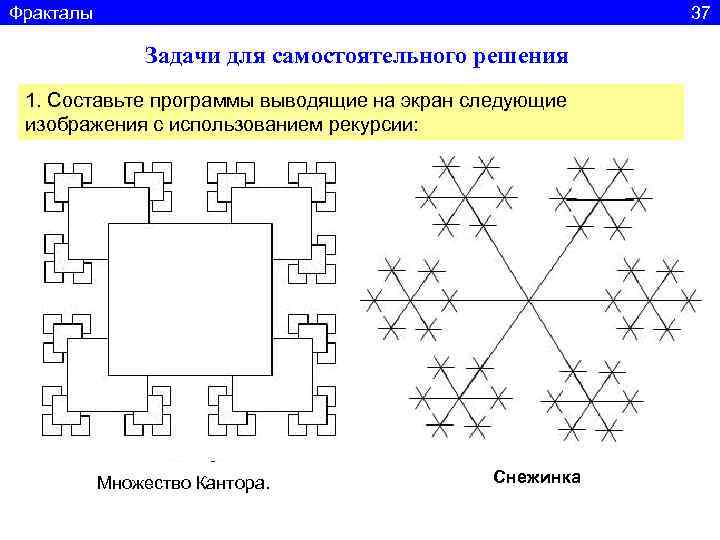
 Фракталы 37 Задачи для самостоятельного решения 1. Составьте программы выводящие на экран следующие изображения с использованием рекурсии: Множество Кантора. Снежинка
Фракталы 37 Задачи для самостоятельного решения 1. Составьте программы выводящие на экран следующие изображения с использованием рекурсии: Множество Кантора. Снежинка
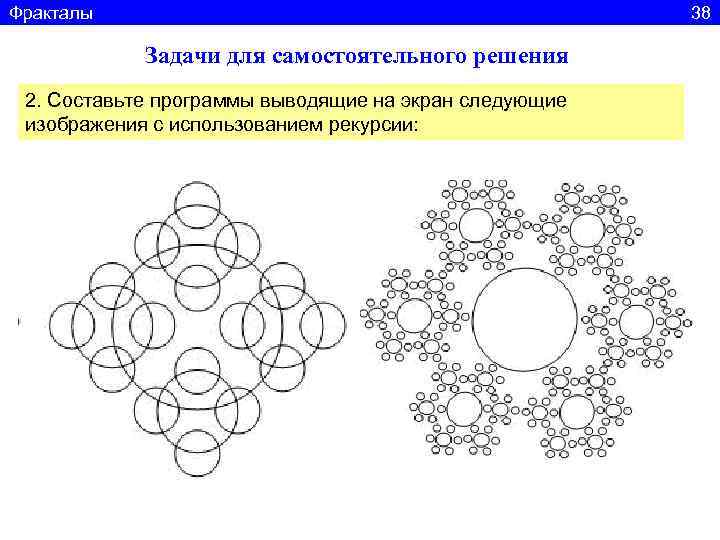
 Фракталы 38 Задачи для самостоятельного решения 2. Составьте программы выводящие на экран следующие изображения с использованием рекурсии:
Фракталы 38 Задачи для самостоятельного решения 2. Составьте программы выводящие на экран следующие изображения с использованием рекурсии:
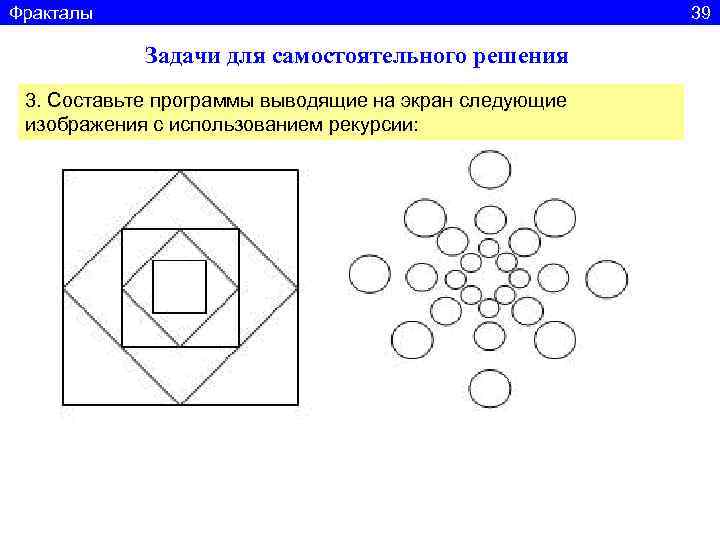
 Фракталы 39 Задачи для самостоятельного решения 3. Составьте программы выводящие на экран следующие изображения с использованием рекурсии:
Фракталы 39 Задачи для самостоятельного решения 3. Составьте программы выводящие на экран следующие изображения с использованием рекурсии:

