Определение положения центра тяжести сечения составленного из стандартных

Определение положения центра тяжести сечения, составленного из стандартных прокатных профилей (двутавров, швеллеров, уголков, полос) Фаюстов Анатолий Афанасьевич доцент кафедры инновационного менеджмента ГУУ

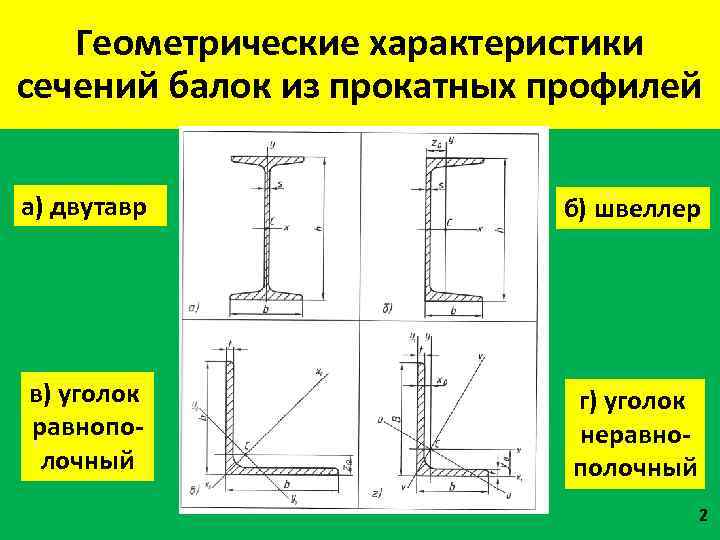Геометрические характеристики сечений балок из прокатных профилей а) двутавр б) швеллер в) уголок равнополочный г) уголок неравнополочный 2

Обозначения h – высота балки (для двутавра и швеллера); b – ширина полки (для двутавра, швеллера и уголков); s – толщина стенки (для двутавра и швеллера); B – ширина большей полки (для неравнополочного уголка); t – толщина полки (для уголков); z 0 – расстояние от центра тяжести, находящегося на оси y-y, до наружной грани стенки (для швеллера) или до наружной грани полки (для равнополочного уголка); x 0, y 0 – расстояние от центра тяжести до наружных граней полок (для неравнополочного уголка). 3

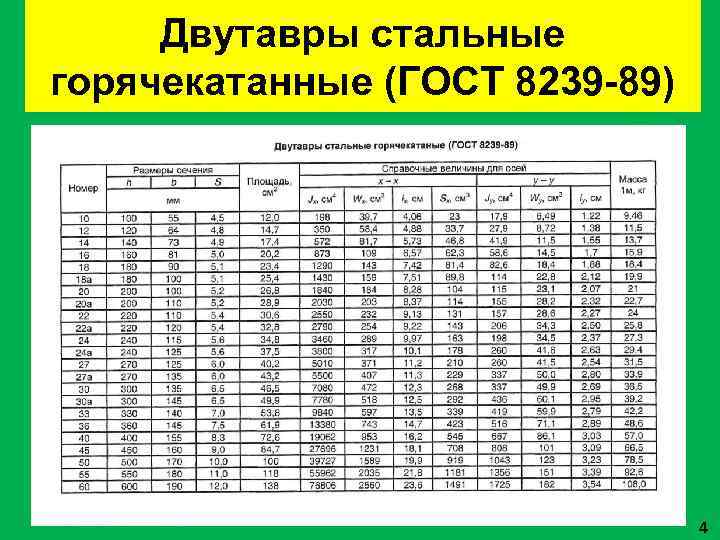Двутавры стальные горячекатанные (ГОСТ 8239 -89) 4

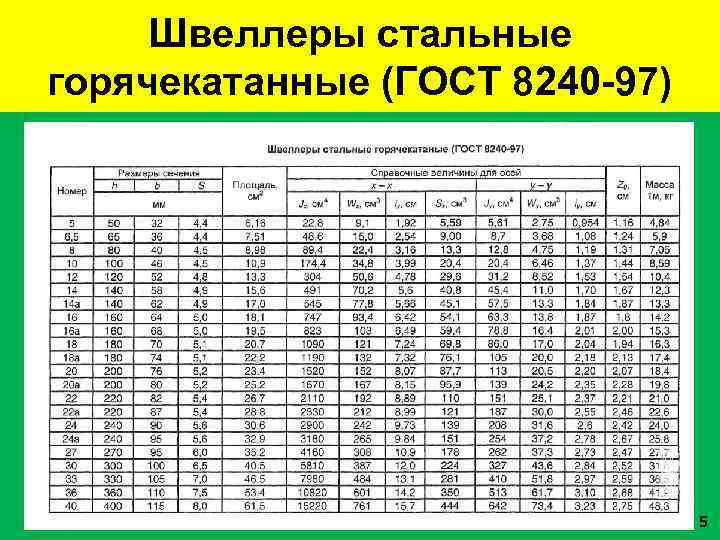Швеллеры стальные горячекатанные (ГОСТ 8240 -97) 5

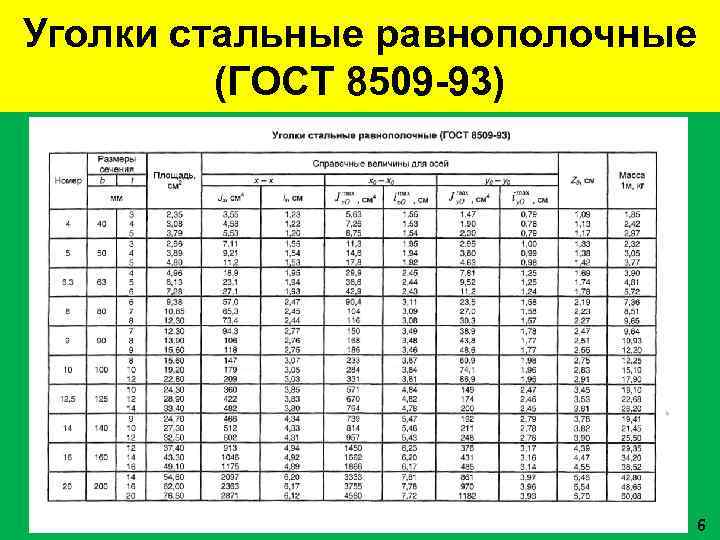Уголки стальные равнополочные (ГОСТ 8509 -93) 6

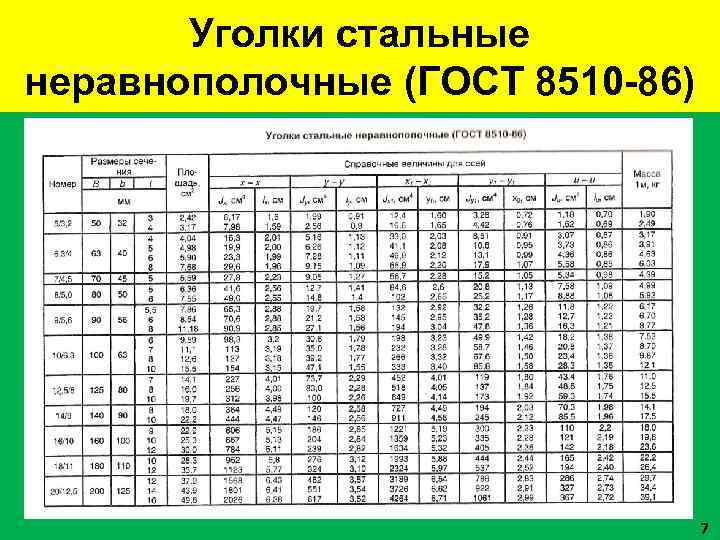Уголки стальные неравнополочные (ГОСТ 8510 -86) 7

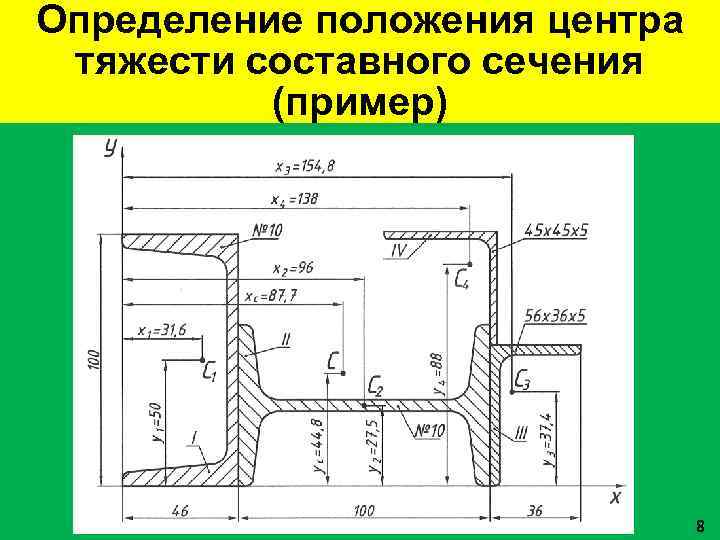Определение положения центра тяжести составного сечения (пример) 8

Определение положения центра тяжести составного сечения (ход решения) Выбираем систему координат так, чтобы сечение было расположено в первом квадранте. Составными частями сечения являются швеллер № 10 (I), двутавр № 10 (II), неравнополочный уголок 56× 36× 5 мм (III), равнополочный уголок 45× 5 мм (IV). Значения площадей и координаты центров тяжести швеллера, двутавра и уголков берем из таблиц прокатной стали ГОСТ 8240 -97, ГОСТ 8239 -89, ГОСТ 8510 -86, ГОСТ 8509 -93. 9

Определение положения центра тяжести составного сечения (ход решения) для швеллера № 10 F 1 = 10, 9 см 2, z 0 = 1, 44 см; для двутавра № 10 F 2 = 12, 0 см 2; для неравнополочного уголка 56× 36× 5 F 3 = 4, 41 см 2, x 0 = 0, 88 см, y 0 = 1, 86 см; для равнополочного уголка 45× 5 F 4 = 4, 29 см 2, z 0 = 1, 30 см. Координаты центров тяжести швеллера, двутавра, уголков указаны на чертеже в миллиметрах. 10

Определение положения центра тяжести составного сечения (окончание) Определяем положение центра тяжести сечения (координата хс): 11

Определение положения центра тяжести составного сечения (окончание) Определяем положение центра тяжести сечения (координата ус): 12

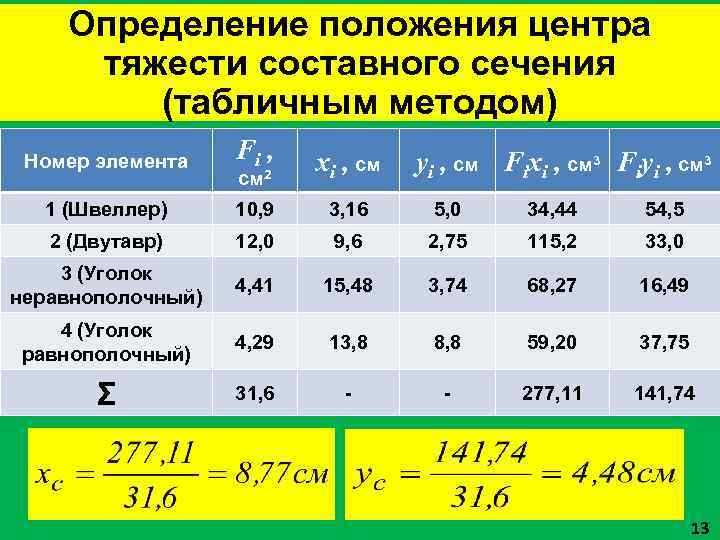Определение положения центра тяжести составного сечения (табличным методом) Номер элемента Fi , см 2 xi , см 1 (Швеллер) 10, 9 3, 16 5, 0 34, 44 54, 5 2 (Двутавр) 12, 0 9, 6 2, 75 115, 2 33, 0 3 (Уголок неравнополочный) 4, 41 15, 48 3, 74 68, 27 16, 49 4 (Уголок равнополочный) 4, 29 13, 8 8, 8 59, 20 37, 75 Σ 31, 6 - - 277, 11 141, 74 yi , см Fixi , см 3 Fiyi , см 3 13