ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ Распределение напряжений

ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В ГРУНТАХ

Распределение напряжений в случае пространственной задачи. Распределение напряжений в случае плоской задачи. Контактная задача (распределение напряжений по подошве сооружений, опирающихся на грунт). Распределение напряжений от собственного веса грунта

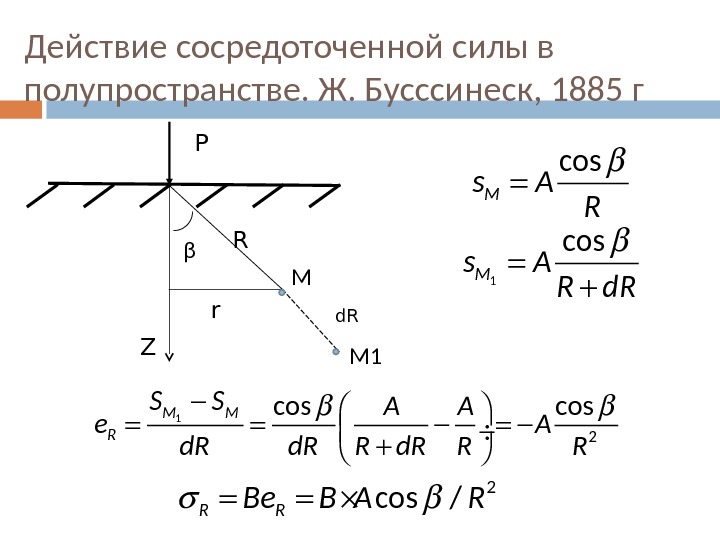
Действие сосредоточенной силы в полупространстве. Ж. Бусссинеск, 1885 г М М 1 d. R Z P β R rcos M s A R 1 cos. M s A R d. R 1 2 cos M M R S S A A e A d. R R R 2 cos /R RBe B A R

Условия равновесия/2 0 0 : cos 0; iz RF Р d. F 2 ( sin ) ; d. F R Rd /23 22 0 0 2 cos 2 sin 2 3 3 2 / 3 0 2 3 cos 2 R P ABсоs d P АВ Р PАВ АВ Р R

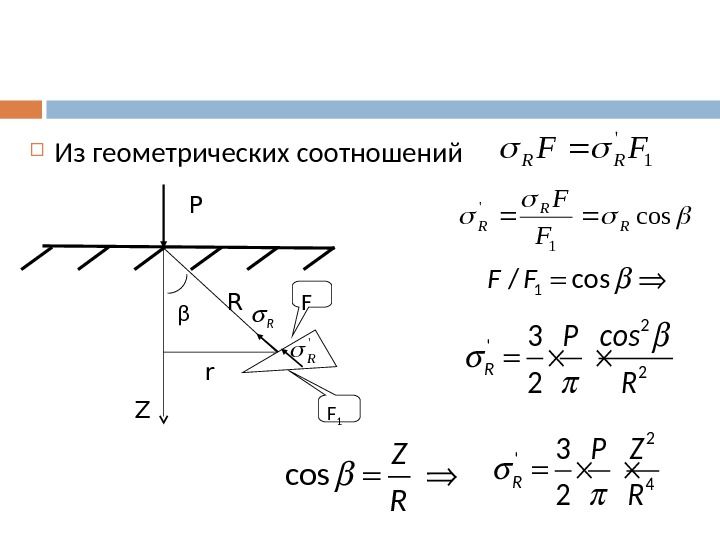
Из геометрических соотношений Z P β R r F 1 F’ R R 1 ‘ FFRR cos 1 ‘ R R R F F 1/ cos. F F 2 ‘ 2 3 2 R Р сos R 2 ‘ 4 3 2 R Р Z R cos Z R

Задача Буссинеска 3 ‘ ‘ ‘ 5 2 2 ‘ ‘ ‘ 5 3 5 2 23 cos ; , 2 3 1 /. 2 z R R R zy R R R zx R R R z P z K R R z y P yz P y y K R R z x P xz P x x K R R z K r z

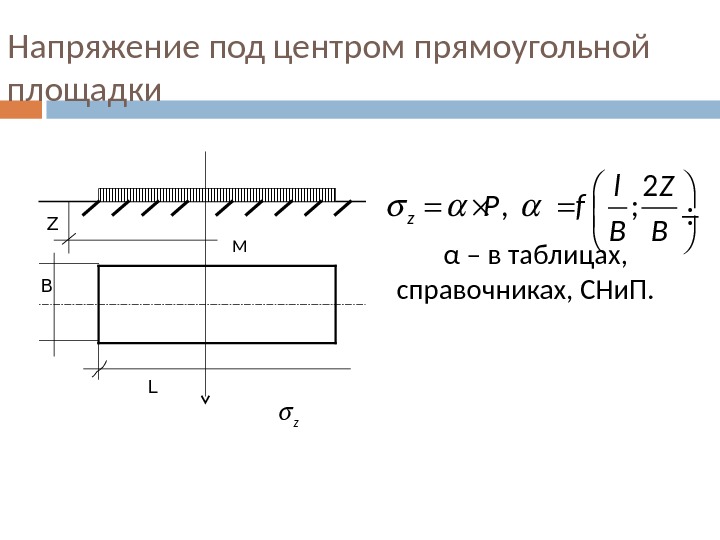
Напряжение под центром прямоугольной площадки α – в таблицах, справочниках, СНи. П. 2 , ; z l Z P f В В Z B L z М

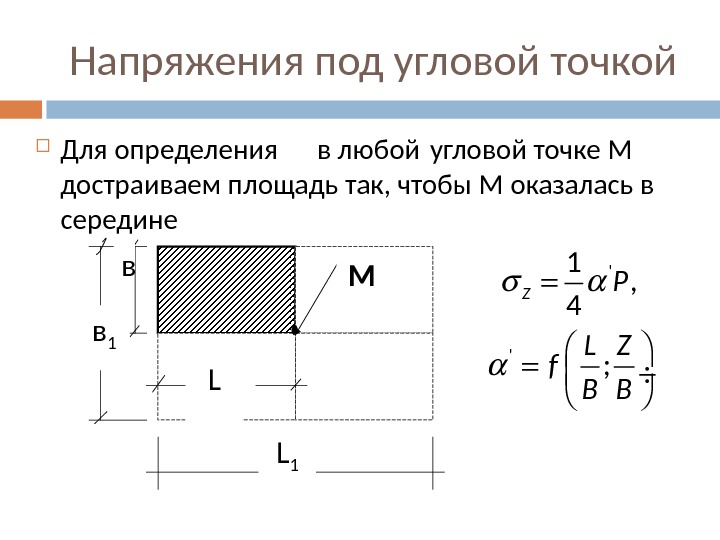
Напряжения под угловой точкой Для определения в любой угловой точке М достраиваем площадь так, чтобы М оказалась в середине L М Lв в 1 ‘ ‘ 1 , 4 ; Z Р L Z f В В L

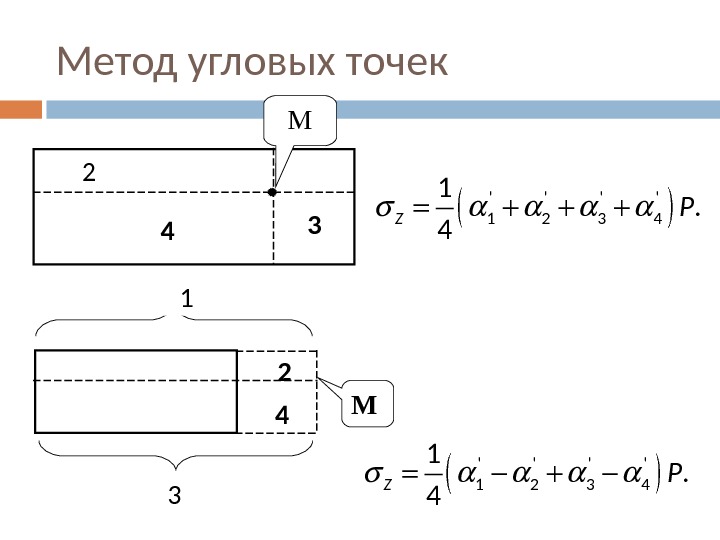
Метод угловых точек 2 4 3 М ‘ ‘ 1 2 3 4 1. 4 ZP 4 2 М 3 1 ‘ ‘ 1 2 3 4 1. 4 ZP

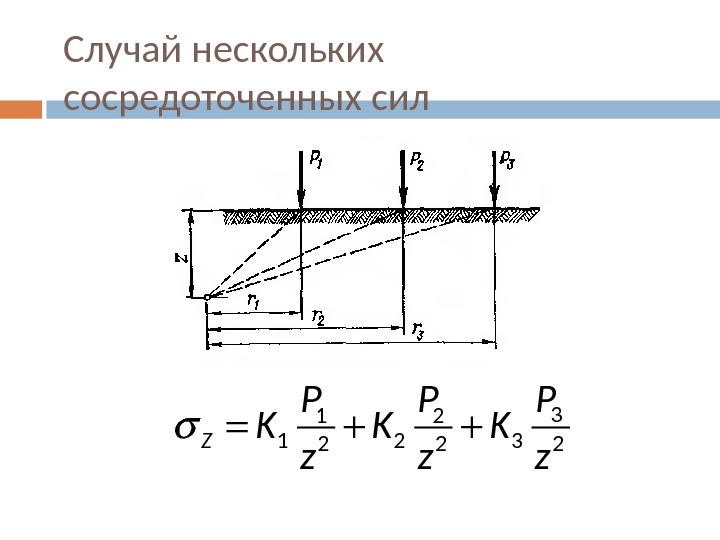
Случай нескольких сосредоточенных сил 3 1 2 3 2 2 2 Z P P P K K K z z z

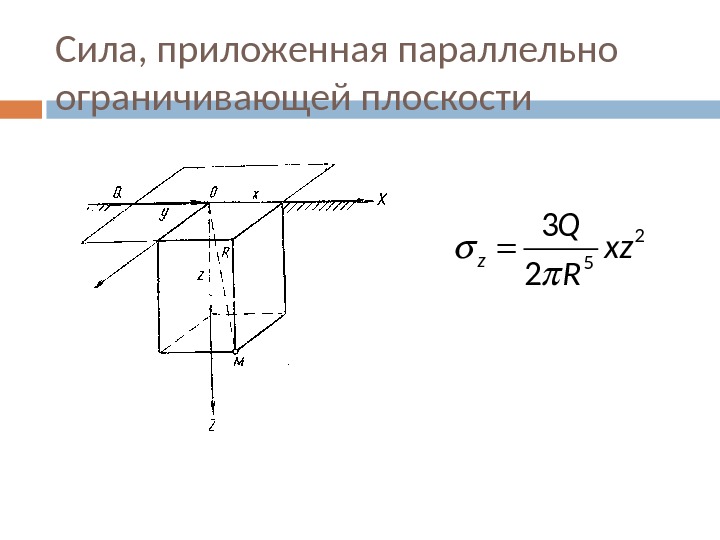
Сила, приложенная параллельно ограничивающей плоскости 2 53 2 z Q xz R

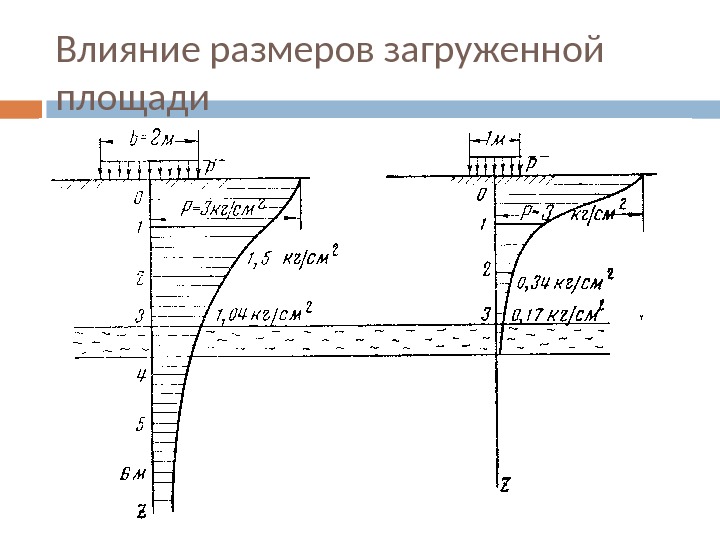
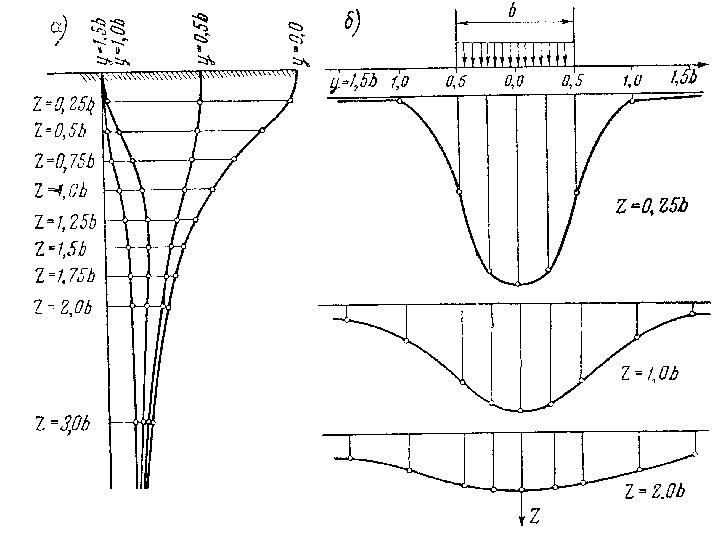
Влияние размеров загруженной площади

РАСПРЕДЕЛЕНИЕ НАПРЯЖЕНИЙ В СЛУЧАЕ ПЛОСКОЙ ЗАДАЧИ

Постановка задачи Напряжения распределяются в одной плоскости и не зависят от координат, перпендикулярных рассматриваемой плоскости – в ленточных фундаментах, подпорных стенках, дорожных насыпях и т. д. Если принять, что по направлению оси х деформации равны нулю, то напряжения σ z , σ y и τ не зависят от деформационных характеристик линейно-деформируемого пространства.

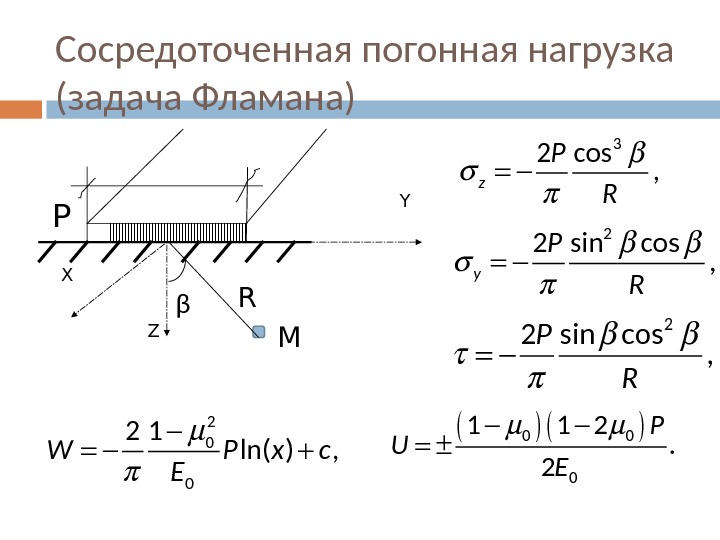
Сосредоточенная погонная нагрузка (задача Фламана) 3 2 cos , z P R 2 2 sin cos , y P R 2 2 sin cos , P R 2 0 01 2 ln( ) , W P x c E 0 0 01 1 2. 2 P U E P X Y Z MR β

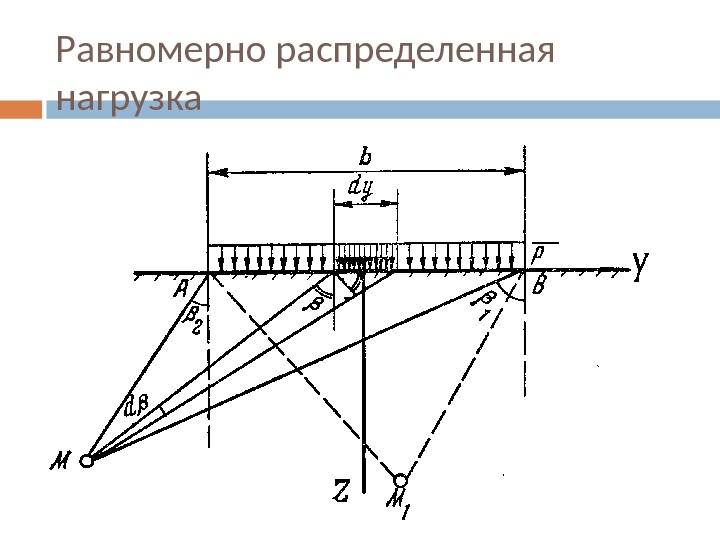
Равномерно распределенная нагрузка

Равномерно распределенная нагрузка 1 2 2 2 2 11 1 sin ( ) sin( 2 ) ; 2 2 cos 2. 2 z y P P P

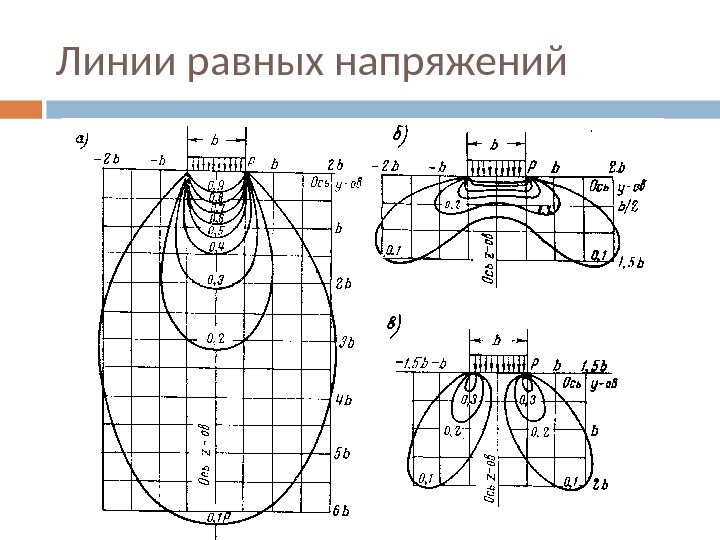
Линии равных напряжений

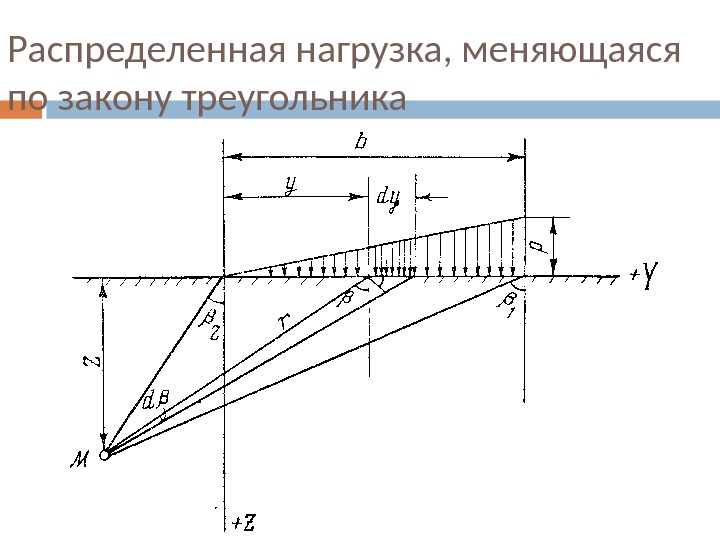
Распределенная нагрузка, меняющаяся по закону треугольника

Распределенная нагрузка, меняющаяся по закону треугольника 2 2 1 1 2 2 [sin 1 1 tg sin 2 ]; 2 2 z Pz b

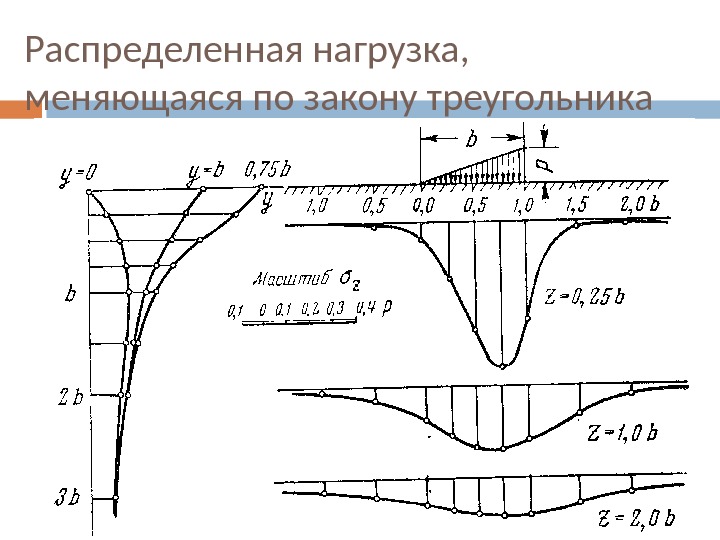
Распределенная нагрузка, меняющаяся по закону треугольника

КОНТАКТНАЯ ЗАДАЧА

Распределение давлений по подошве сооружений Задача Буссинеска В общем случае Для абсолютно жесткого фундамента w=cosnt 0 , P w C R 2 2 01 ( , ) ( ) F p d d w C x y

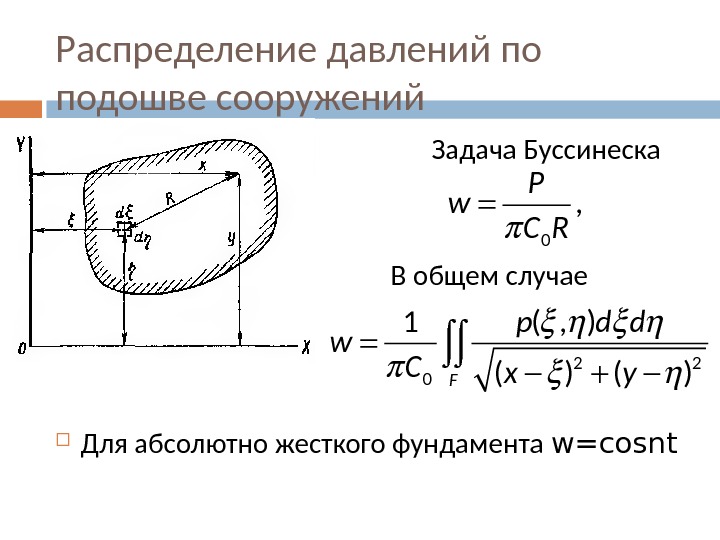
Распределение давлений по подошве сооружений При круглой площади подошвы r – радиус подошвы фундамента, — расстояние от центра подошвы до любой ее точки, — среднее давление на единицу площади подошвы. Для плоской задачи y – расстояние по горизонтали от середины фундамента до рассматриваемой точки, — полуширина фундамента. 2 / 2 1 / , xy mp p r mp 2 12 / 1 / , xy mp p y b 1 b

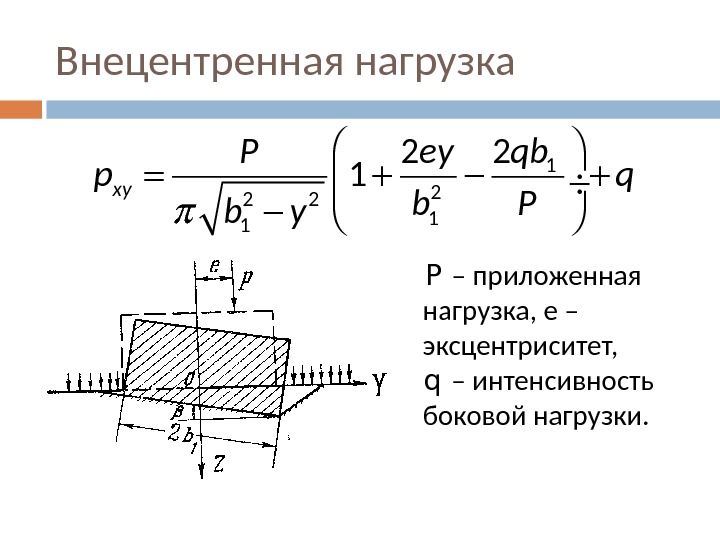
Внецентренная нагрузка P – приложенная нагрузка, е – эксцентриситет, q – интенсивность боковой нагрузки. 1 2 2 2 1 1 2 2 1 xy qb P ey p q b P b y

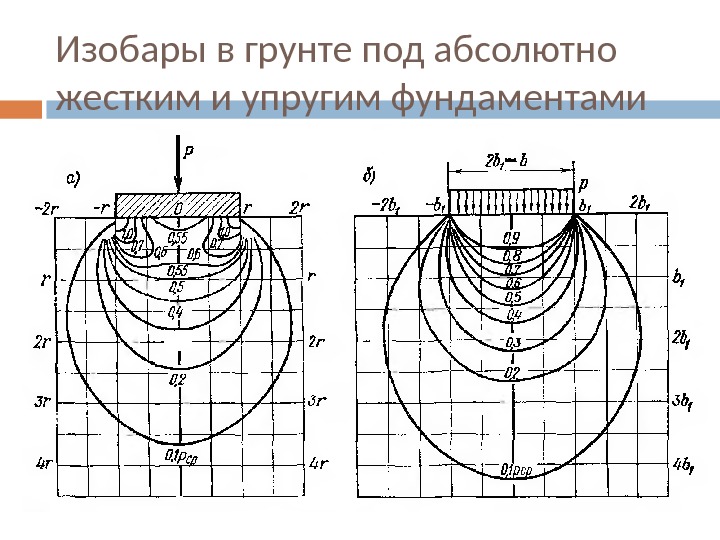
Изобары в грунте под абсолютно жестким и упругим фундаментами

Начальные напряжения Силы гравитации (собственный вес) Увеличение или уменьшение грунтовой толщи Тектонические, сейсмические воздействия Работы нулевого цикла (выемка грунта, трамбование)

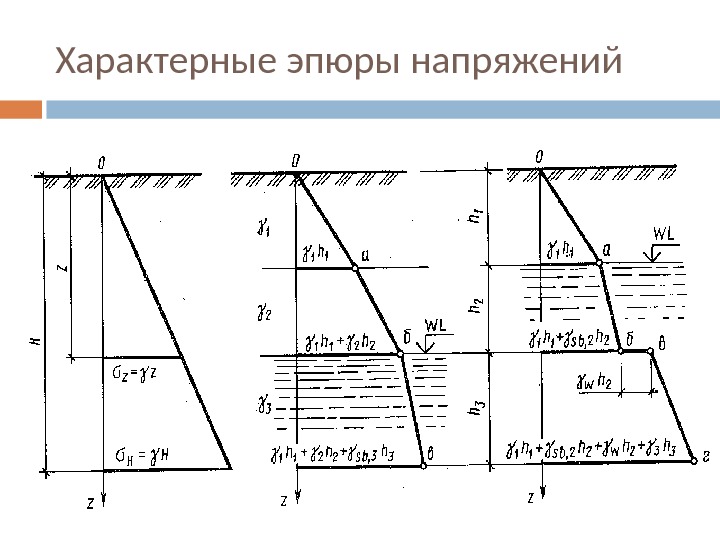
Распределение напряжений от собственного веса грунта Если учитывать только силы гравитации 0 0 0; 0. коэффициент бокового давления 1 z z z x y z zy yz zx dz

Характерные эпюры напряжений

Удельный вес грунта во взвешенном состоянии 1 s w sb e