Определение момента силы относительно точки в плоскости Составитель

Определение момента силы относительно точки в плоскости Составитель: Абдюкова Рима Явдатовна. кафедра Механики и технологии машиностроения

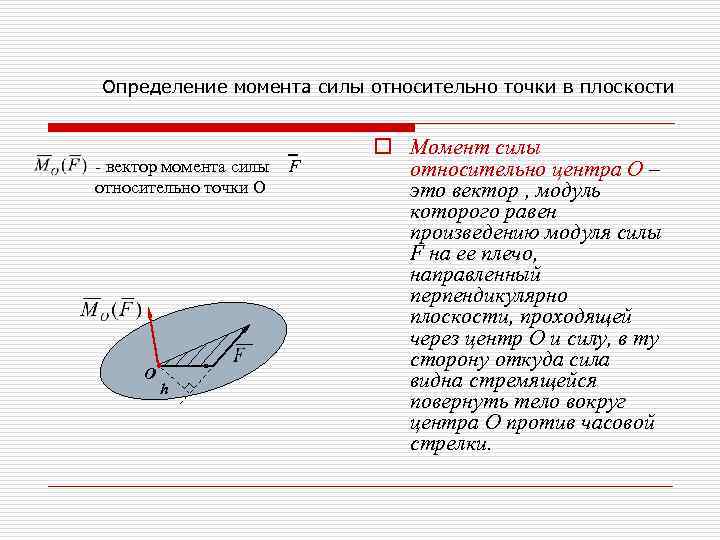Определение момента силы относительно точки в плоскости - вектор момента силы F относительно точки О О h o Момент силы относительно центра О – это вектор , модуль которого равен произведению модуля силы F на ее плечо, направленный перпендикулярно плоскости, проходящей через центр О и силу, в ту сторону откуда сила видна стремящейся повернуть тело вокруг центра О против часовой стрелки.

Определение момента силы относительно точки в плоскости Точка О – центр момента О o Если вектор силы и моментная точка лежат в одной плоскости (в случае плоской произвольной системы сил), то можно считать момент силы относительно центра алгебраической величиной.

Практическое занятие Определение момента силы относительно точки в плоскости o Центр момента – это точка, относительно которой берется момент. Точка О – центр момента О

Практическое занятие Определение момента силы относительно точки в плоскости Прямая АВ – линия действия силы В О А o Линия действия силы – это прямая, вдоль которой действует сила.

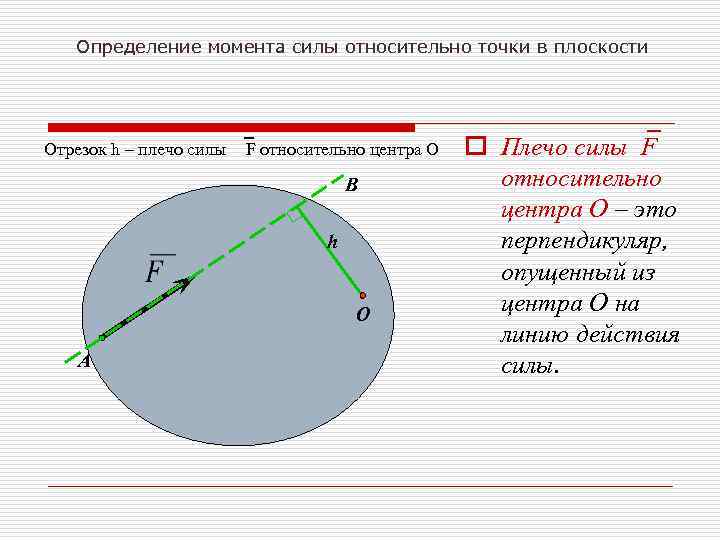Определение момента силы относительно точки в плоскости Отрезок h – плечо силы F относительно центра О В h О А o Плечо силы F относительно центра О – это перпендикуляр, опущенный из центра О на линию действия силы.

Определение момента силы относительно точки в плоскости В h О А o Момент силы относительно центра О – это алгебраическая величина, значение которой равно произведению модуля силы F на ее плечо.

Определение момента силы относительно точки в плоскости О + О - o Момент силы относительно центра считается положительным, если сила видна стремящейся повернуть тело против часовой стрелки, и отрицательным, - если по часовой стрелке.

Практическое занятие Свойства момента силы относительно точки в плоскости В В h А О o Момент силы относительно центра не изменится при переносе точки приложения силы вдоль линии ее действия.

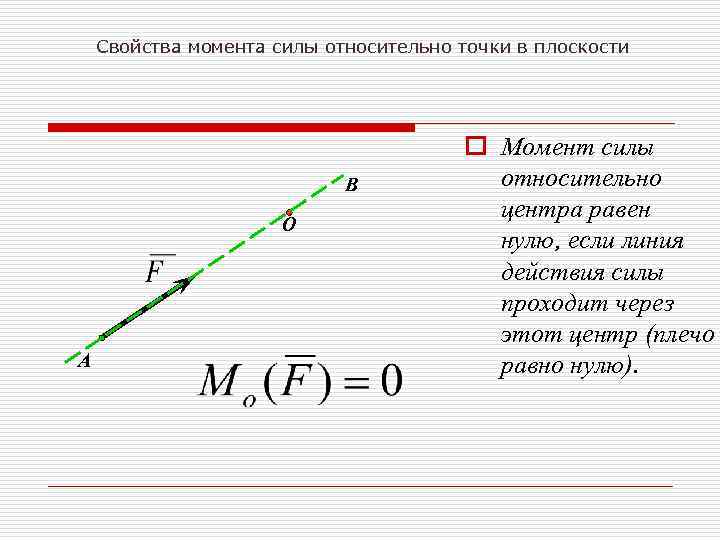Свойства момента силы относительно точки в плоскости В О А o Момент силы относительно центра равен нулю, если линия действия силы проходит через этот центр (плечо равно нулю).

Применение теоремы Вариньона для определения момента силы относительно точки o Если сила не параллельна координатным осям, то для определения ее момента относительно точки удобно воспользоваться теоремой Вариньона. О Fy а F в МО( F) = -a·F ·cos -b·F·sin Fx 1. Для этого силу нужно разложить на проекции: F = Fx + Fy 2. Момент силы F относительно точки О можно представить суммой моментов составляющих сил относительно той же точки: МО( F) = МО( Fx)+ МО( Fy)

Пример Определить моменты сил относительно точки О Сила F 1 раскладывается на проекции: F 1 30 F 1 = F 1 х+ F 1 y Fy 1 Значение проекций: F 1 x= F 1 ·cos 300 Fx 1 О F 1 у= F 1 ·sin 300 в а Плечо к проекции F 1 x относительно точки О равно в, знак момента «+» . с F 2 Плечо к проекции F 1 у относительно точки О равно а, знак момента «+» . Момент силы F 1 относительно точки О представляем суммой моментов МО( F 1 ) = в·F ·cos 300 +а·F·sin 300

Пример Определить моменты сил относительно точки О F 1 30 Сила F 2 параллельна оси Ох, для определения ее момента не требуется применение теоремы Вариньона. Fy 1 Fx 1 О Плечо к силе F 2 относительно точки О равно с, знак момента «-» . в а Момент силы F 2 относительно точки О равен с F 2 МO( F 2 )= - c·F 2