Скачать презентацию Определение автокорреляции Автокорреляция характеризуется тем что не выполняется Скачать презентацию Определение автокорреляции Автокорреляция характеризуется тем что не выполняется

8 autocorrelation.ppt

  • Количество слайдов: 29

Определение автокорреляции Автокорреляция характеризуется тем, что не выполняется одно из условий Гаусса. Маркова: Определение автокорреляции Автокорреляция характеризуется тем, что не выполняется одно из условий Гаусса. Маркова:

Причины автокорреляции Обычно автокорреляция встречается в регрессионном анализе при использовании временных рядов. Для временных Причины автокорреляции Обычно автокорреляция встречается в регрессионном анализе при использовании временных рядов. Для временных рядов предположение о некоррелированности ошибок часто не выполняется, так как результаты предыдущих наблюдений влияют на результаты следующих.

Причины чистой автокорреляции Примеры: 1. y — последовательность значений курса ценной бумаги; t — Причины чистой автокорреляции Примеры: 1. y — последовательность значений курса ценной бумаги; t — время. Результаты предыдущих торгов влияют на результаты последующих

Причины чистой автокорреляции Примеры: 2. y — спрос на мороженое; x — доход потребителей. Причины чистой автокорреляции Примеры: 2. y — спрос на мороженое; x — доход потребителей. Данные фиксировались ежемесячно в течение нескольких лет. y лето Положительная автокорреляция лето зима x

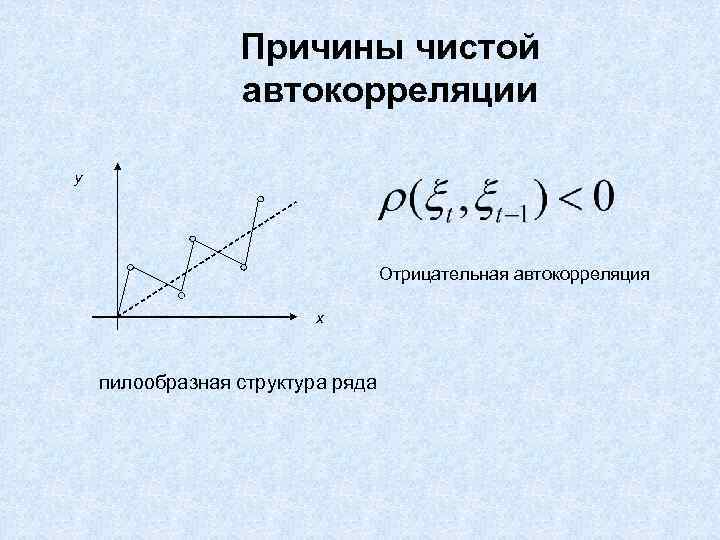Причины чистой автокорреляции y Отрицательная автокорреляция x пилообразная структура ряда Причины чистой автокорреляции y Отрицательная автокорреляция x пилообразная структура ряда

Автокорреляция первого порядка случайная составляющая рассматриваемого уравнения регрессии, коэффициент автокорреляции первого порядка, случайная составляющая, Автокорреляция первого порядка случайная составляющая рассматриваемого уравнения регрессии, коэффициент автокорреляции первого порядка, случайная составляющая, независимы

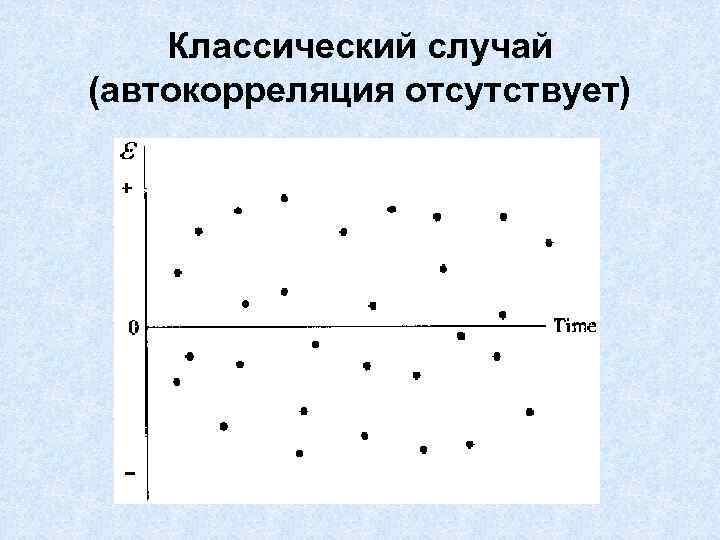Классический случай (автокорреляция отсутствует) Классический случай (автокорреляция отсутствует)

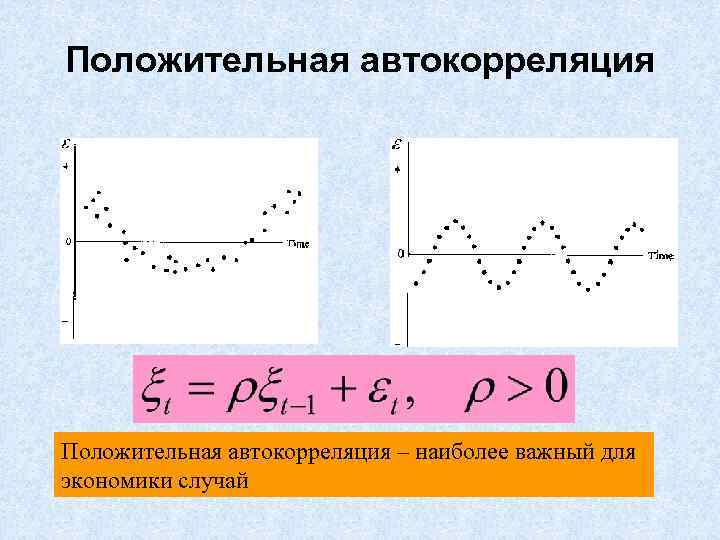Положительная автокорреляция – наиболее важный для экономики случай Положительная автокорреляция – наиболее важный для экономики случай

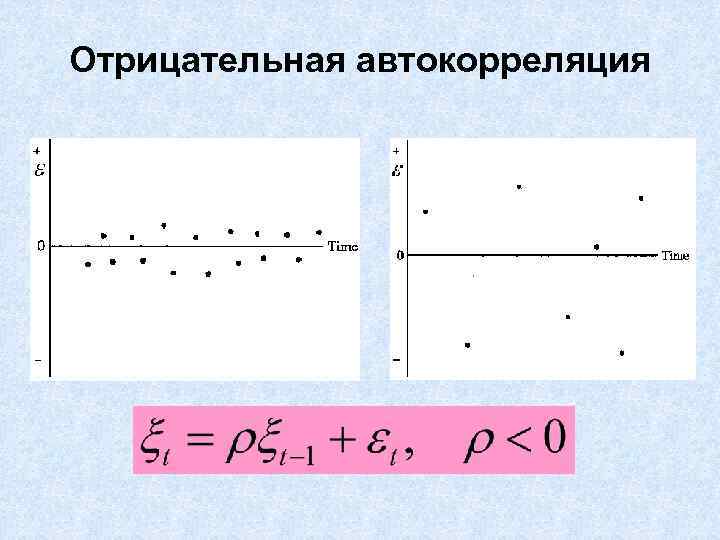Отрицательная автокорреляция Отрицательная автокорреляция

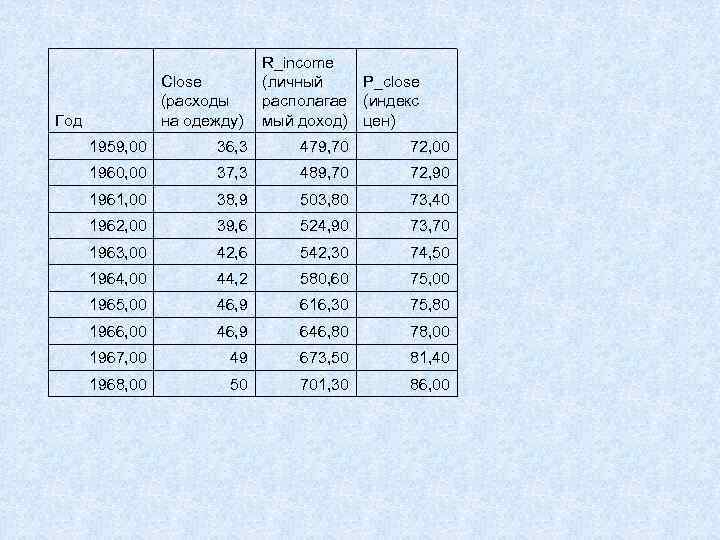Close (расходы на одежду) Год R_income (личный P_close располагае (индекс мый доход) цен) 1959, Close (расходы на одежду) Год R_income (личный P_close располагае (индекс мый доход) цен) 1959, 00 36, 3 479, 70 72, 00 1960, 00 37, 3 489, 70 72, 90 1961, 00 38, 9 503, 80 73, 40 1962, 00 39, 6 524, 90 73, 70 1963, 00 42, 6 542, 30 74, 50 1964, 00 44, 2 580, 60 75, 00 1965, 00 46, 9 616, 30 75, 80 1966, 00 46, 9 646, 80 78, 00 1967, 00 49 673, 50 81, 40 1968, 00 50 701, 30 86, 00

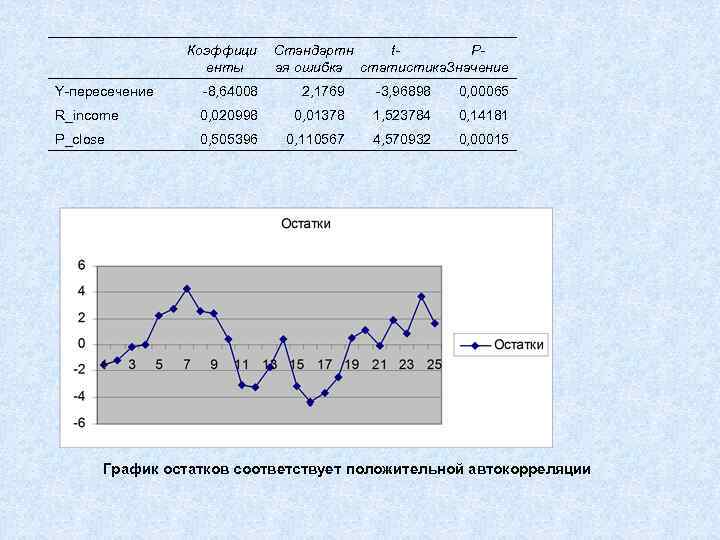Коэффици енты Стандартн t. Pая ошибка статистика. Значение Y-пересечение -8, 64008 2, 1769 Коэффици енты Стандартн t. Pая ошибка статистика. Значение Y-пересечение -8, 64008 2, 1769 -3, 96898 0, 00065 R_income 0, 020998 0, 01378 1, 523784 0, 14181 P_close 0, 505396 0, 110567 4, 570932 0, 00015 График остатков соответствует положительной автокорреляции

Последствия автокорреляции 1. Оценки несмещенные, состоятельные, но неэффективные. 2. Стандартные ошибки занижены, tстатистики завышены. Последствия автокорреляции 1. Оценки несмещенные, состоятельные, но неэффективные. 2. Стандартные ошибки занижены, tстатистики завышены. Поэтому выводы по оценке качества коэффициентов и модели в целом, возможно, будут неверными.

Обнаружение автокорреляции 1. Графический метод. 2. Критерий знаков. 3. Критерий Дарбина-Уотсона. 4. Тест серий Обнаружение автокорреляции 1. Графический метод. 2. Критерий знаков. 3. Критерий Дарбина-Уотсона. 4. Тест серий (Бреуша-Годфри) В специализированных эконометрических пакетах эти тесты есть

Тест Дарбина-Уотсона. 1. Вычислить остатки Тест Дарбина-Уотсона. 1. Вычислить остатки

Тест Дарбина-Уотсона. 1. Вычислить остатки 2. Вычислить оценку коэффициента автокорреляции остатков Остатки со сдвигом Тест Дарбина-Уотсона. 1. Вычислить остатки 2. Вычислить оценку коэффициента автокорреляции остатков Остатки со сдвигом -1, 521 -1, 18583 -1, 521 -0, 13459 -1, 18583 -0, 02926 -0, 13459 2, 201064 -0, 02926 2, 744158 2, 201064 4, 290227 2, 744158 2, 537928 4, 290227 Данные – Анализ данных –Корреляция Столбец 1 1 Столбец 2 0, 715853 Столбец 2 1

Статистика Дарбина-Уотсона 3. Вычислить статистику Дарбина. Уотсона: Статистика Дарбина-Уотсона 3. Вычислить статистику Дарбина. Уотсона:

Границы для статистики Дарбина. Уотсона Если , то Границы для статистики Дарбина. Уотсона Если , то

Критические точки распределения Дарбина-Уотсона 4. Для более точного определения, какое значение DW свидетельствует об Критические точки распределения Дарбина-Уотсона 4. Для более точного определения, какое значение DW свидетельствует об отсутствии автокорреляции, а какое – о ее наличии, построена таблица критических точек распределения Дарбина-Уотсона. По этой таблице для заданного уровня значимости , числа наблюдений n и числа регрессоров k определяются два значения: dн – нижняя граница, dв – верхняя граница

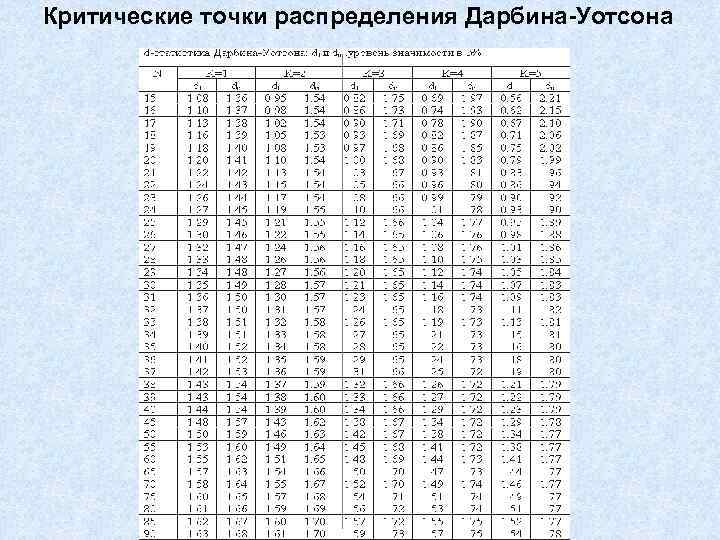Критические точки распределения Дарбина-Уотсона Критические точки распределения Дарбина-Уотсона

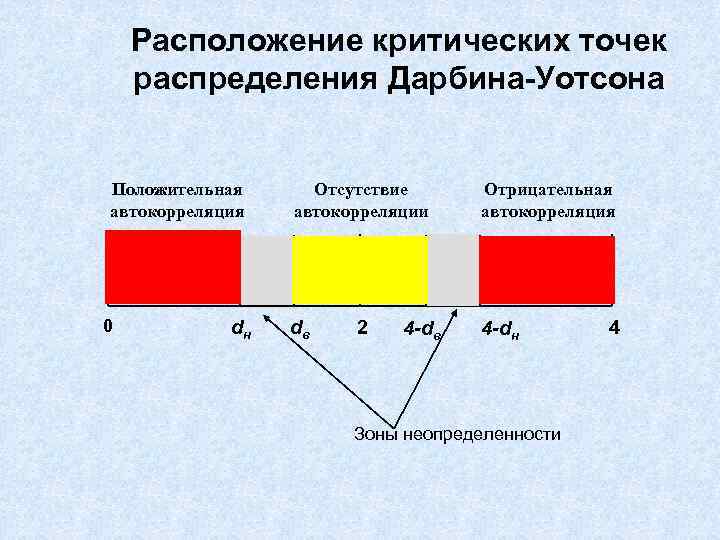Расположение критических точек распределения Дарбина-Уотсона Положительная автокорреляция 0 dн Отсутствие автокорреляции Отрицательная автокорреляция dв Расположение критических точек распределения Дарбина-Уотсона Положительная автокорреляция 0 dн Отсутствие автокорреляции Отрицательная автокорреляция dв 4 -dн 2 4 -dв Зоны неопределенности 4

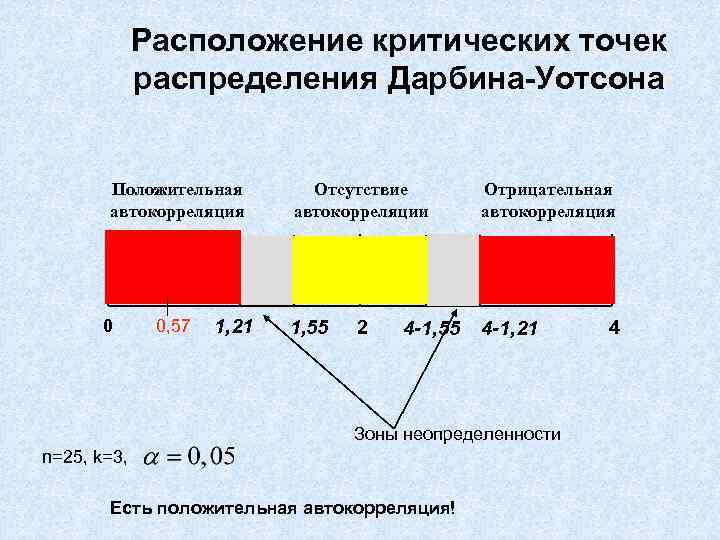Расположение критических точек распределения Дарбина-Уотсона Положительная автокорреляция 0 0, 57 1, 21 Отсутствие автокорреляции Расположение критических точек распределения Дарбина-Уотсона Положительная автокорреляция 0 0, 57 1, 21 Отсутствие автокорреляции Отрицательная автокорреляция 1, 55 4 -1, 21 2 4 -1, 55 Зоны неопределенности n=25, k=3, Есть положительная автокорреляция! 4

Устранение автокорреляции — независимы Устранение автокорреляции — независимы

Устранение автокорреляции первого порядка (при известном коэффициенте автокорреляции) В модели (3) выполнены условия Гаусса Устранение автокорреляции первого порядка (при известном коэффициенте автокорреляции) В модели (3) выполнены условия Гаусса – Маркова и можно применять МНК

Устранение автокорреляции (процедура Кохрейна-Оркатта) 1. Вычислить остатки 2. Вычислить коэффициент автокорреляции остатков 3. Создать Устранение автокорреляции (процедура Кохрейна-Оркатта) 1. Вычислить остатки 2. Вычислить коэффициент автокорреляции остатков 3. Создать переменные: 4. Оценить модель 5. Вычислить 6. Записать уравнение модели

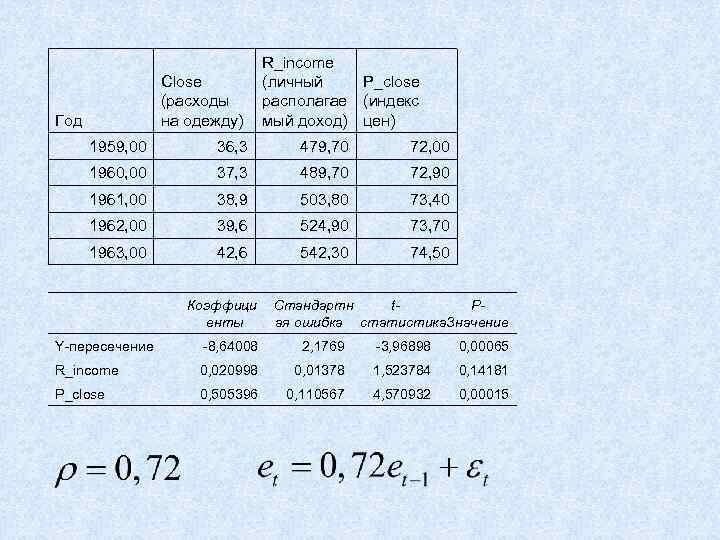Close (расходы на одежду) Год R_income (личный P_close располагае (индекс мый доход) цен) 1959, Close (расходы на одежду) Год R_income (личный P_close располагае (индекс мый доход) цен) 1959, 00 36, 3 479, 70 72, 00 1960, 00 37, 3 489, 70 72, 90 1961, 00 38, 9 503, 80 73, 40 1962, 00 39, 6 524, 90 73, 70 1963, 00 42, 6 542, 30 74, 50 Коэффици енты Стандартн t. Pая ошибка статистика. Значение Y-пересечение -8, 64008 2, 1769 -3, 96898 0, 00065 R_income 0, 020998 0, 01378 1, 523784 0, 14181 P_close 0, 505396 0, 110567 4, 570932 0, 00015

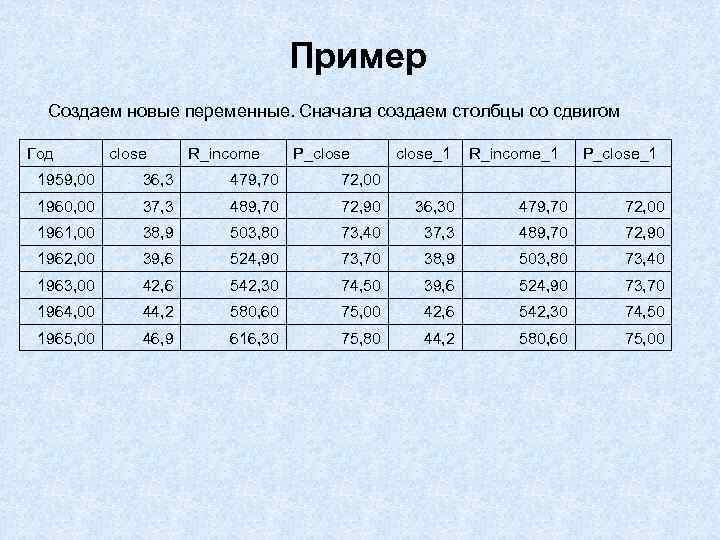Пример Создаем новые переменные. Сначала создаем столбцы со сдвигом Год close R_income P_close_1 R_income_1 Пример Создаем новые переменные. Сначала создаем столбцы со сдвигом Год close R_income P_close_1 R_income_1 P_close_1 1959, 00 36, 3 479, 70 72, 00 1960, 00 37, 3 489, 70 72, 90 36, 30 479, 70 72, 00 1961, 00 38, 9 503, 80 73, 40 37, 3 489, 70 72, 90 1962, 00 39, 6 524, 90 73, 70 38, 9 503, 80 73, 40 1963, 00 42, 6 542, 30 74, 50 39, 6 524, 90 73, 70 1964, 00 44, 2 580, 60 75, 00 42, 6 542, 30 74, 50 1965, 00 46, 9 616, 30 75, 80 44, 2 580, 60 75, 00

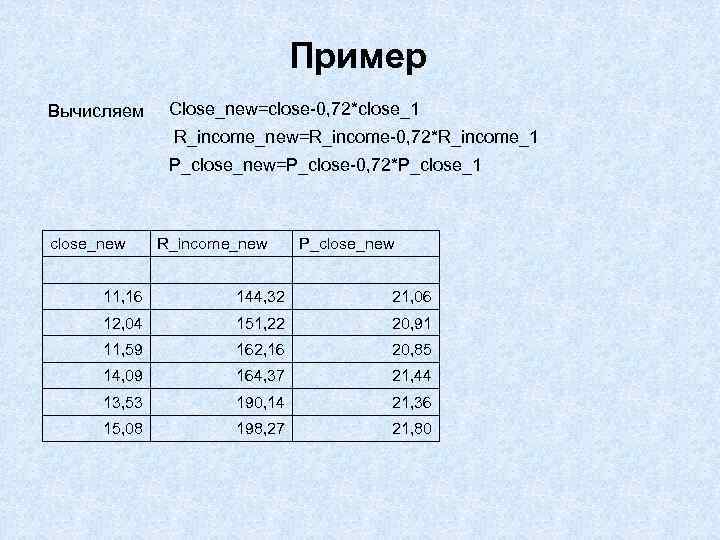Пример Close_new=close-0, 72*close_1 Вычисляем R_income_new=R_income-0, 72*R_income_1 P_close_new=P_close-0, 72*P_close_1 close_new R_income_new P_close_new 11, 16 144, Пример Close_new=close-0, 72*close_1 Вычисляем R_income_new=R_income-0, 72*R_income_1 P_close_new=P_close-0, 72*P_close_1 close_new R_income_new P_close_new 11, 16 144, 32 21, 06 12, 04 151, 22 20, 91 11, 59 162, 16 20, 85 14, 09 164, 37 21, 44 13, 53 190, 14 21, 36 15, 08 198, 27 21, 80

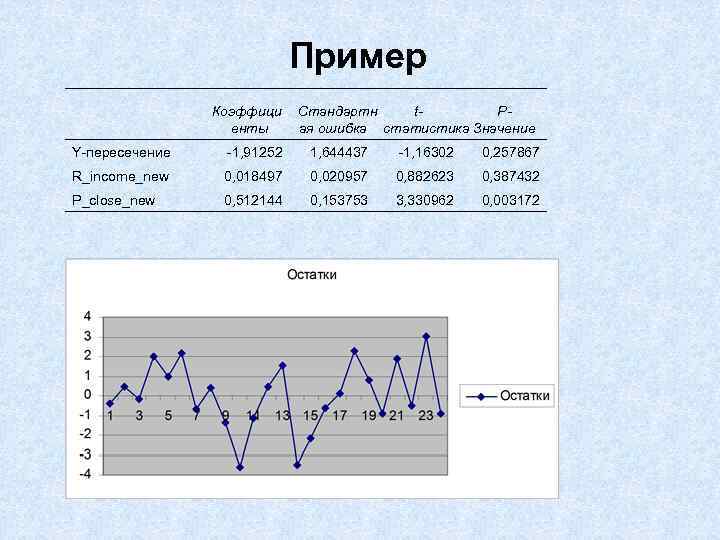Пример Коэффици енты Стандартн t. Pая ошибка статистика Значение Y-пересечение -1, 91252 1, 644437 Пример Коэффици енты Стандартн t. Pая ошибка статистика Значение Y-пересечение -1, 91252 1, 644437 -1, 16302 0, 257867 R_income_new 0, 018497 0, 020957 0, 882623 0, 387432 P_close_new 0, 512144 0, 153753 3, 330962 0, 003172

Пример Коэффици енты Стандартн t. Pая ошибка статистика Значение Y-пересечение -1, 91252 1, 644437 Пример Коэффици енты Стандартн t. Pая ошибка статистика Значение Y-пересечение -1, 91252 1, 644437 -1, 16302 0, 257867 R_income_new 0, 018497 0, 020957 0, 882623 0, 387432 P_close_new 0, 512144 0, 153753 3, 330962 0, 003172 Close=0, 02 * R_Income+0, 51 * P_close-6, 82