radio.pptx
- Количество слайдов: 74
 ОПОРНЫЙ КОНСПЕКТ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Студент Группа Преподаватель
ОПОРНЫЙ КОНСПЕКТ ПО НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ Студент Группа Преподаватель
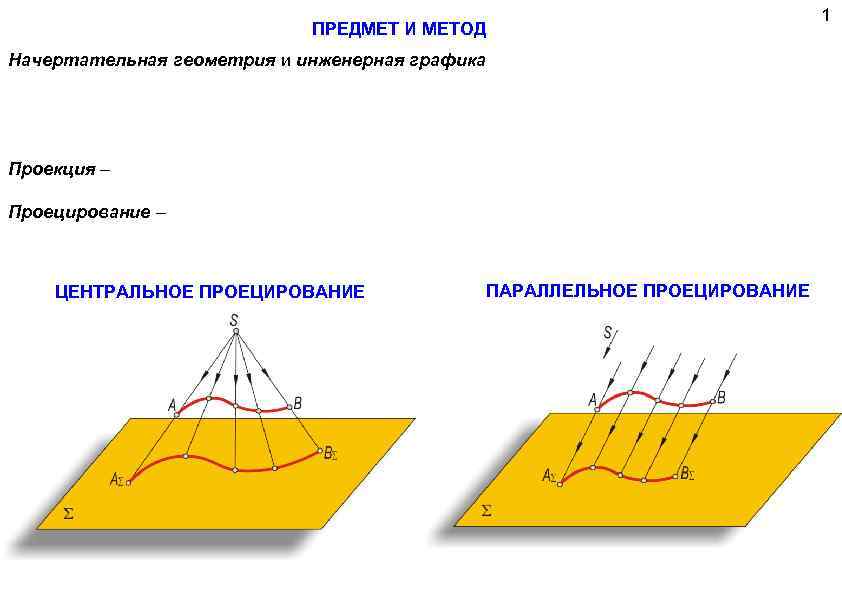 ПРЕДМЕТ И МЕТОД Начертательная геометрия и инженерная графика Основным методом построения изображений на плоскости является метод проекций. Проекция – Проецирование – ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ 1
ПРЕДМЕТ И МЕТОД Начертательная геометрия и инженерная графика Основным методом построения изображений на плоскости является метод проекций. Проекция – Проецирование – ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ 1
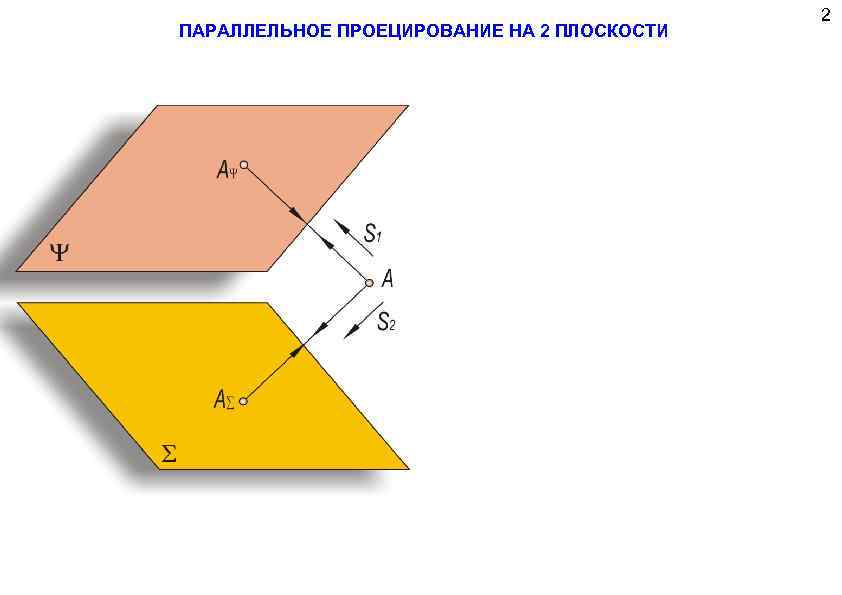 ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ НА 2 ПЛОСКОСТИ 2
ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ НА 2 ПЛОСКОСТИ 2
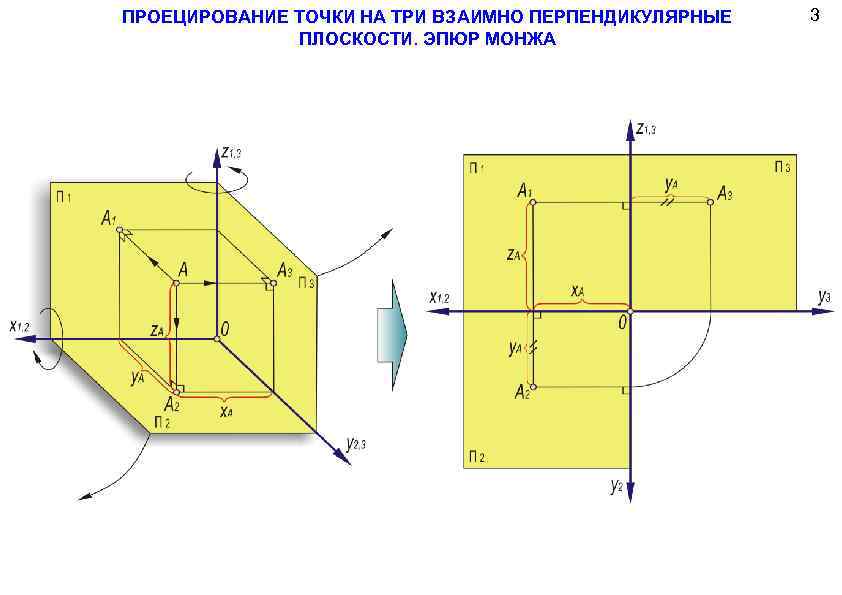 ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ. ЭПЮР МОНЖА 3
ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫЕ ПЛОСКОСТИ. ЭПЮР МОНЖА 3
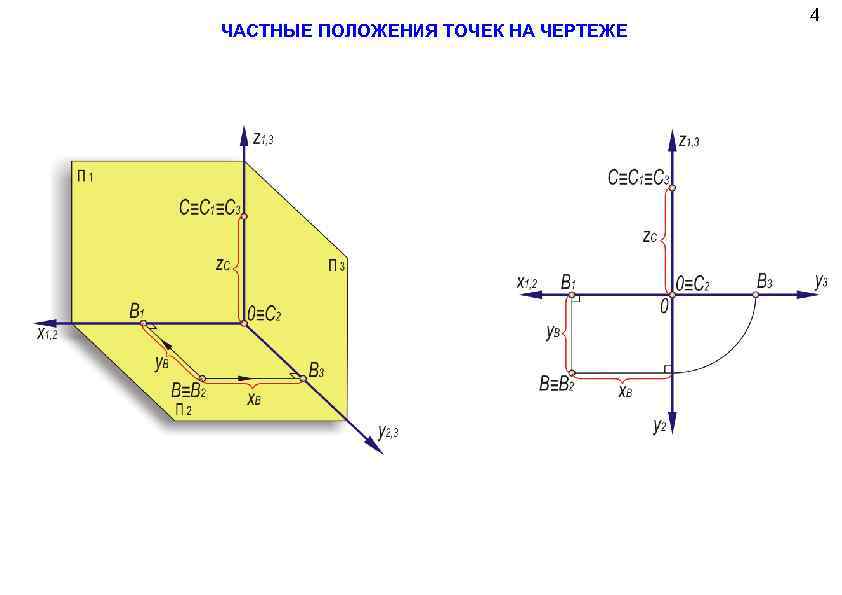 ЧАСТНЫЕ ПОЛОЖЕНИЯ ТОЧЕК НА ЧЕРТЕЖЕ 4
ЧАСТНЫЕ ПОЛОЖЕНИЯ ТОЧЕК НА ЧЕРТЕЖЕ 4
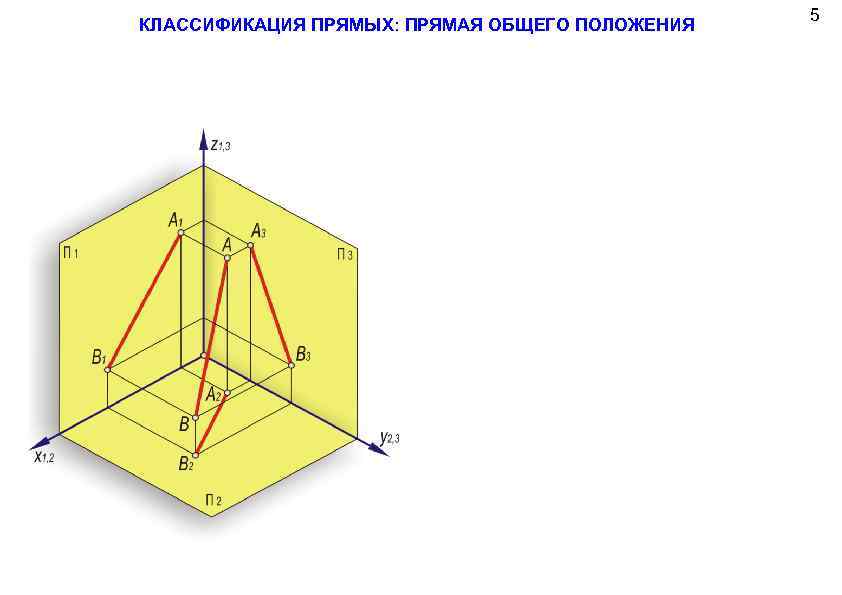 КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ 5
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМАЯ ОБЩЕГО ПОЛОЖЕНИЯ 5
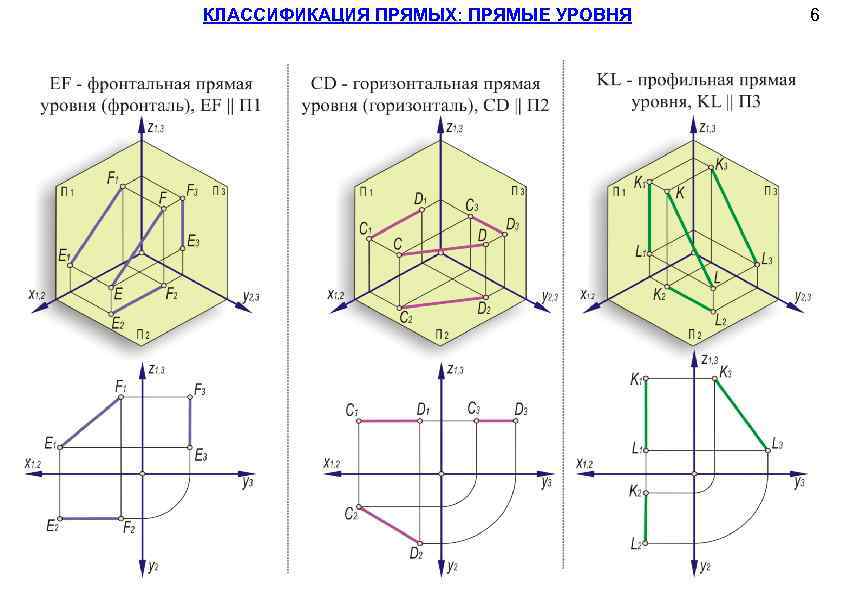 КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМЫЕ УРОВНЯ 6
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРЯМЫЕ УРОВНЯ 6
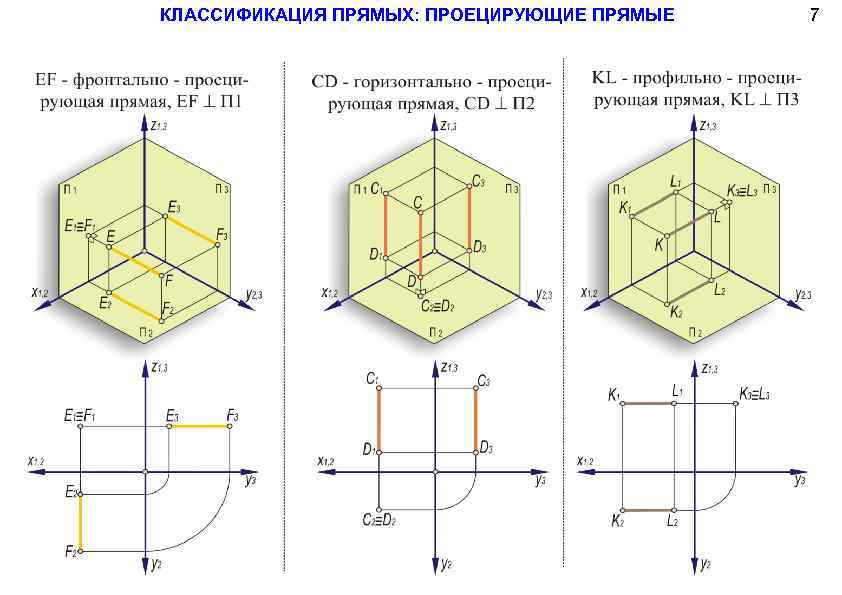 КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ 7
КЛАССИФИКАЦИЯ ПРЯМЫХ: ПРОЕЦИРУЮЩИЕ ПРЯМЫЕ 7
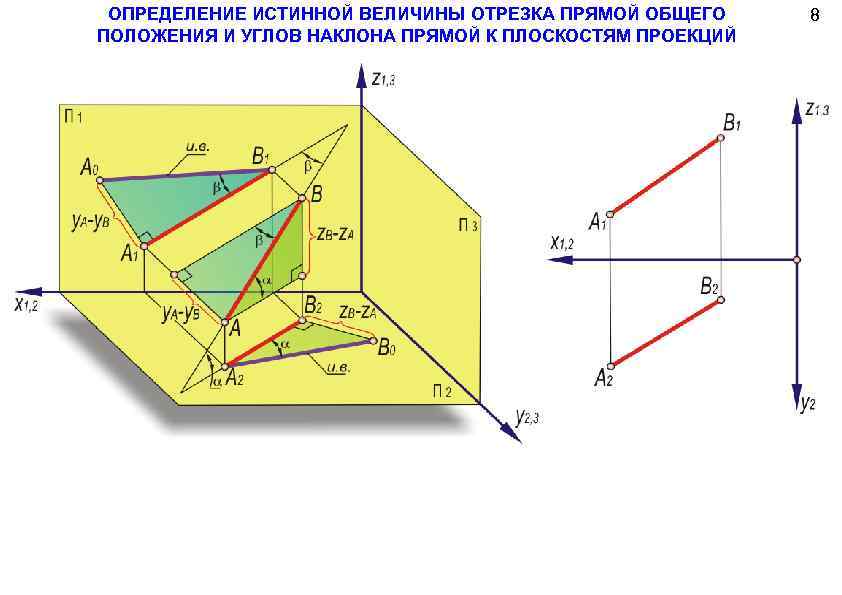 ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ 8
ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ И УГЛОВ НАКЛОНА ПРЯМОЙ К ПЛОСКОСТЯМ ПРОЕКЦИЙ 8
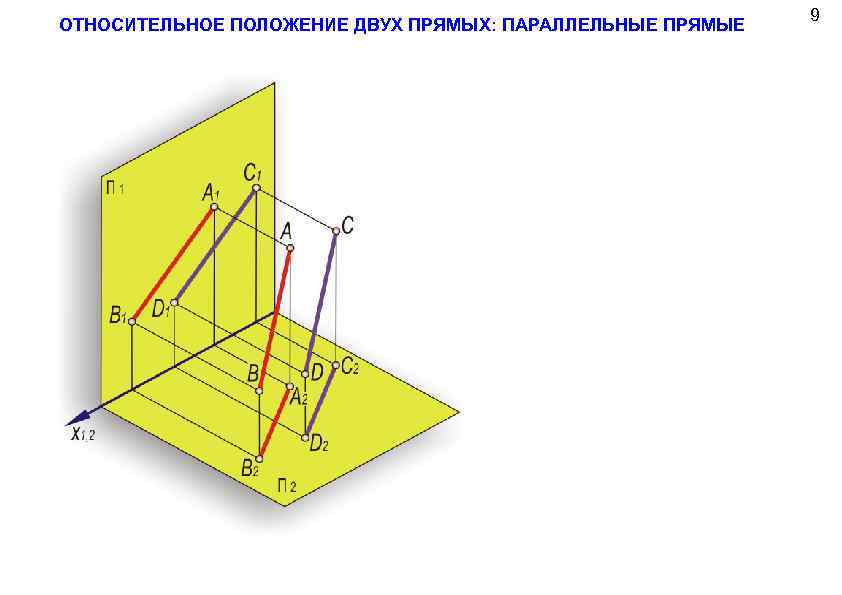 ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ 9
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ 9
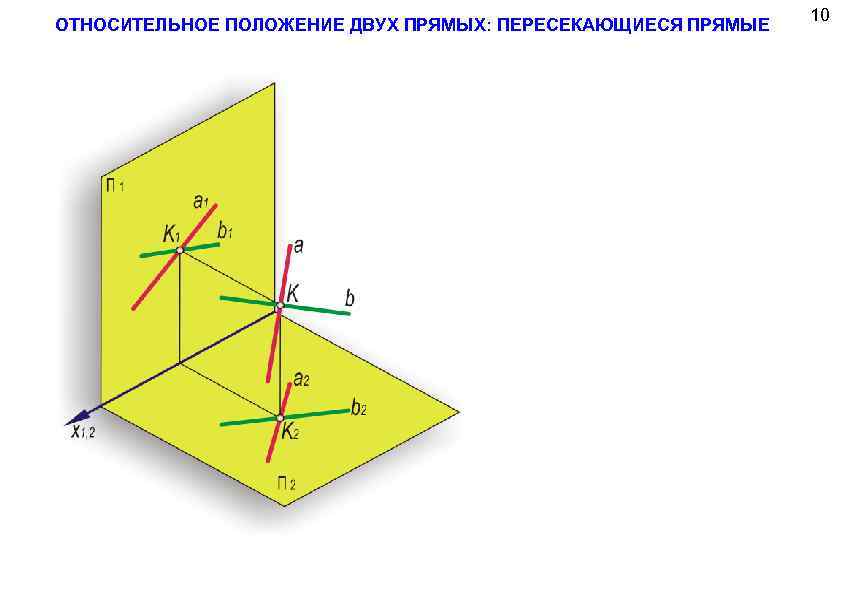 ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ 10
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: ПЕРЕСЕКАЮЩИЕСЯ ПРЯМЫЕ 10
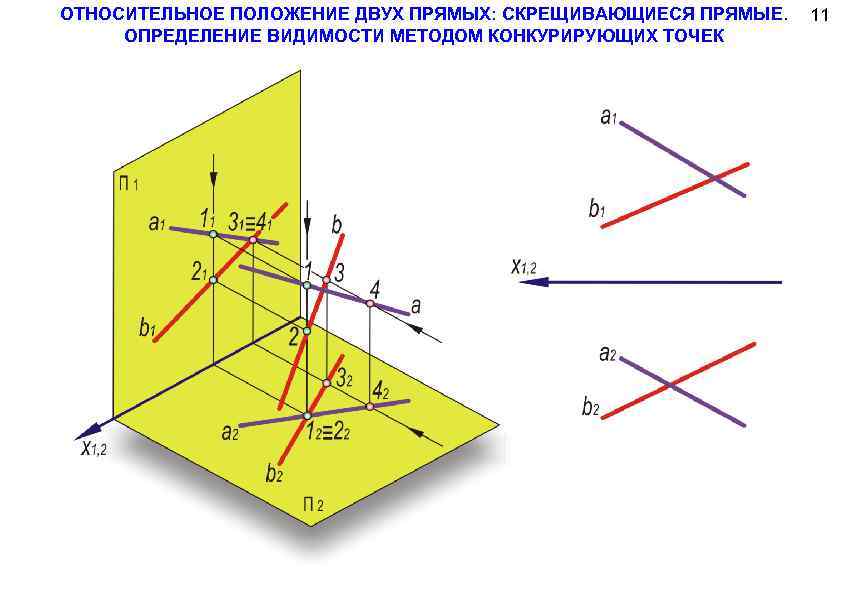 ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ МЕТОДОМ КОНКУРИРУЮЩИХ ТОЧЕК 11
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ДВУХ ПРЯМЫХ: СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ. ОПРЕДЕЛЕНИЕ ВИДИМОСТИ МЕТОДОМ КОНКУРИРУЮЩИХ ТОЧЕК 11
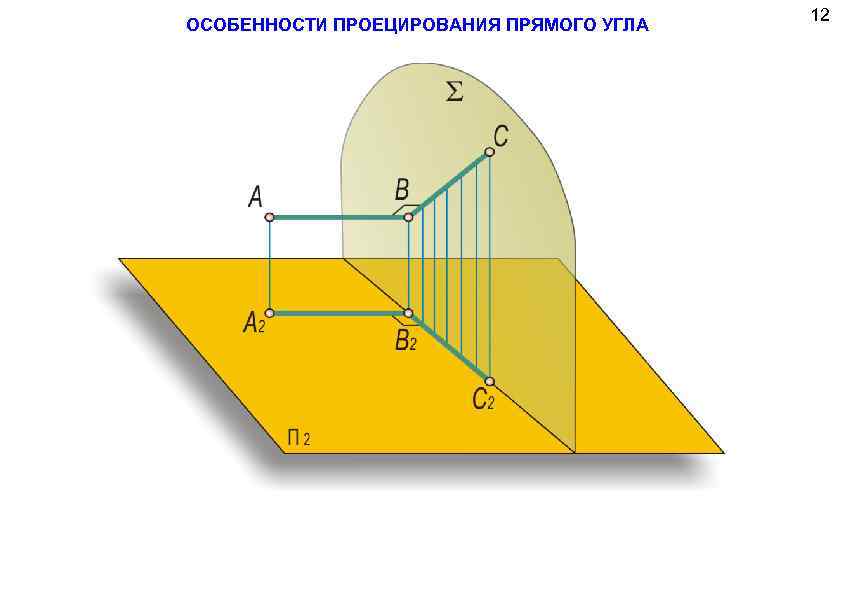 ОСОБЕННОСТИ ПРОЕЦИРОВАНИЯ ПРЯМОГО УГЛА 12
ОСОБЕННОСТИ ПРОЕЦИРОВАНИЯ ПРЯМОГО УГЛА 12
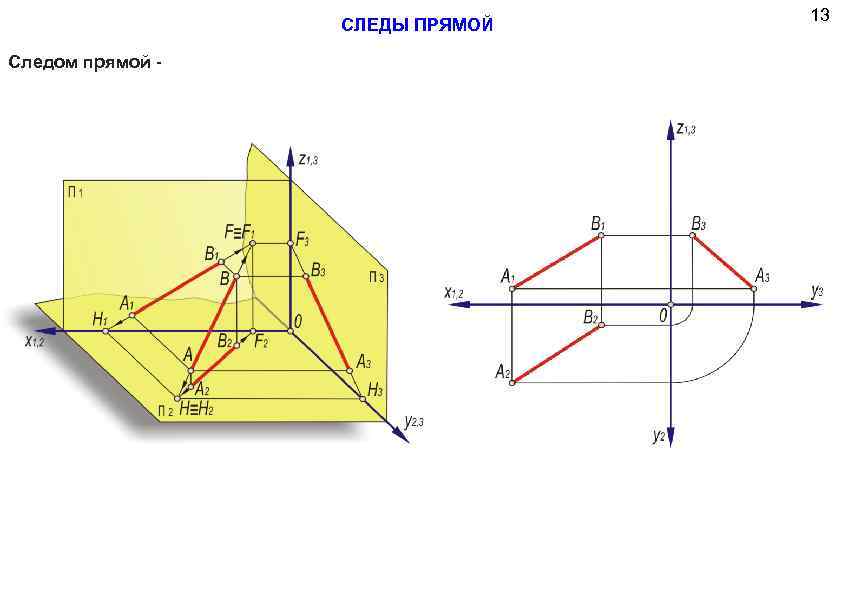 СЛЕДЫ ПРЯМОЙ Следом прямой -. 13
СЛЕДЫ ПРЯМОЙ Следом прямой -. 13
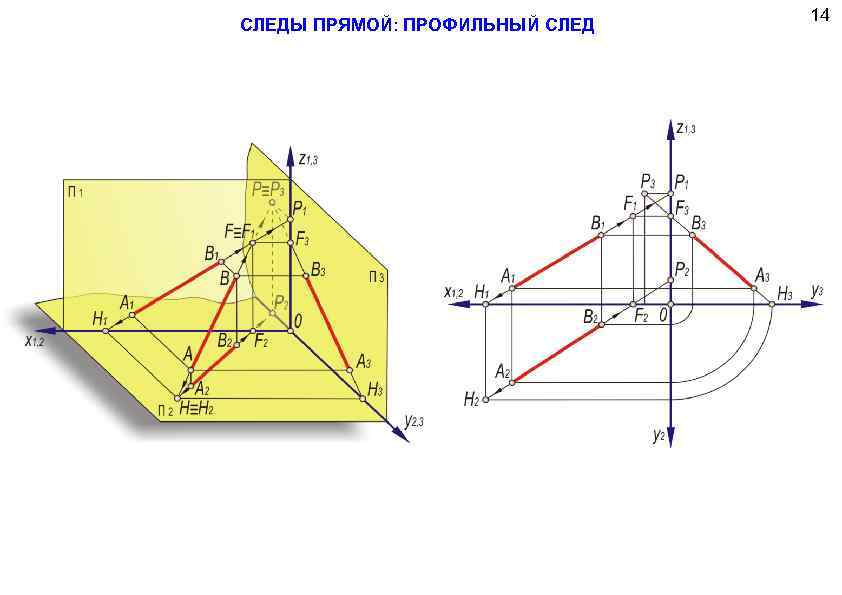 СЛЕДЫ ПРЯМОЙ: ПРОФИЛЬНЫЙ СЛЕД 14
СЛЕДЫ ПРЯМОЙ: ПРОФИЛЬНЫЙ СЛЕД 14
 СПОСОБЫ ИЗОБРАЖЕНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ Плоскость 15
СПОСОБЫ ИЗОБРАЖЕНИЯ ПЛОСКОСТИ НА ЧЕРТЕЖЕ Плоскость 15
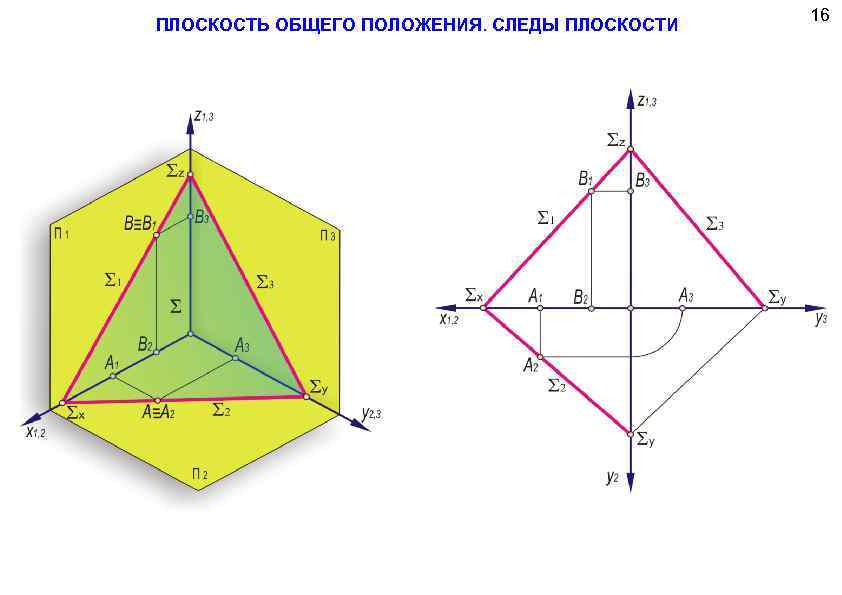 ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ. СЛЕДЫ ПЛОСКОСТИ 16
ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ. СЛЕДЫ ПЛОСКОСТИ 16
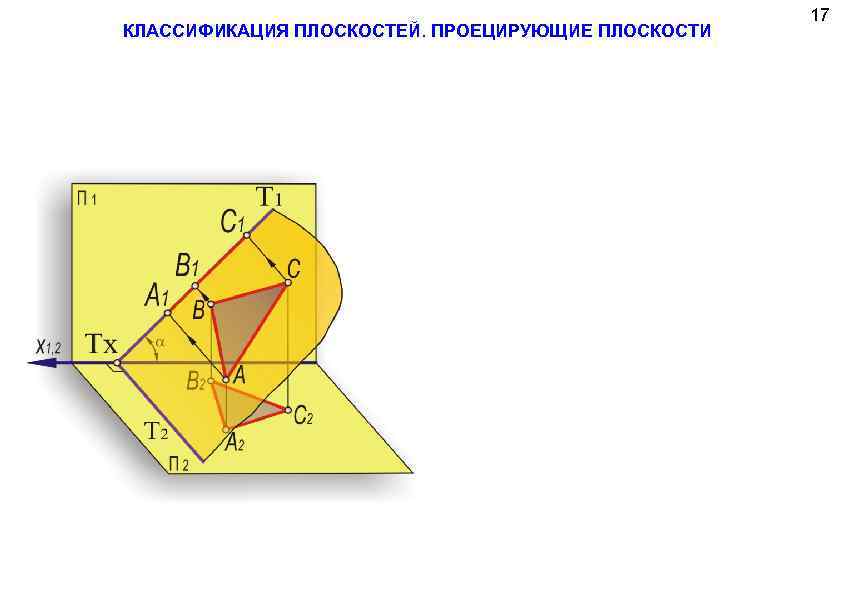 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 17
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 17
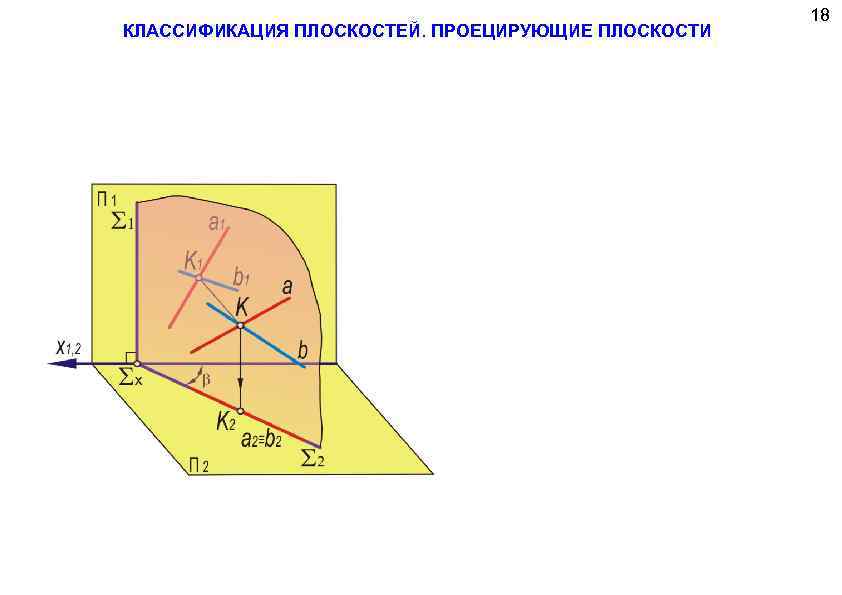 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 18
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 18
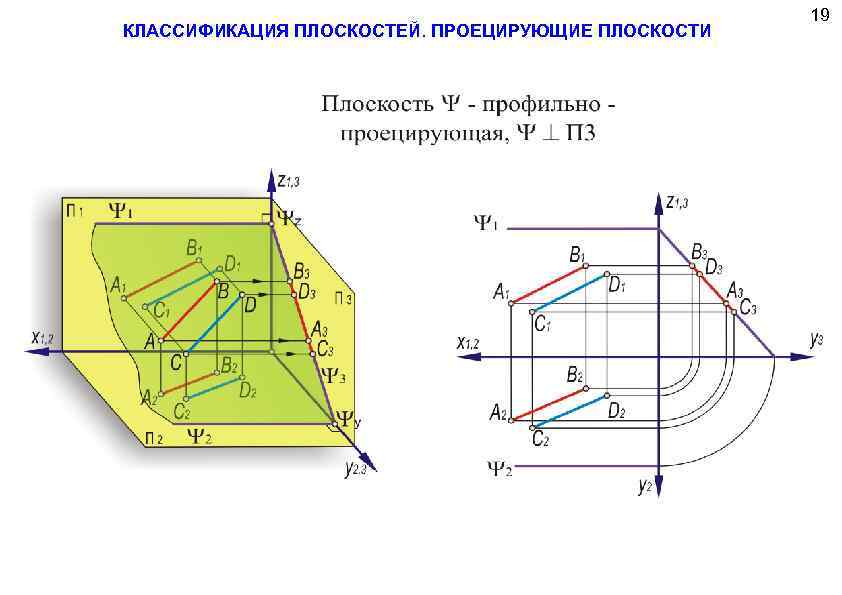 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 19
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ 19
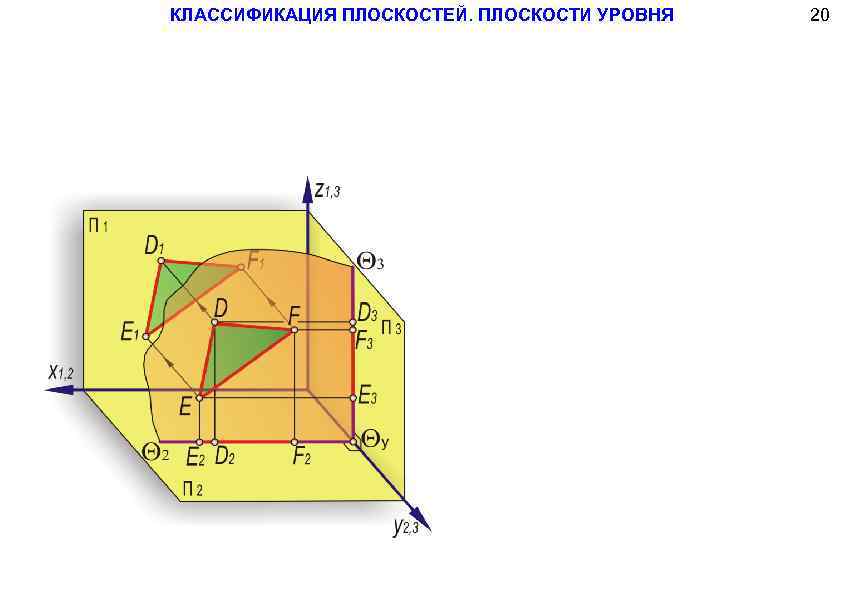 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 20
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 20
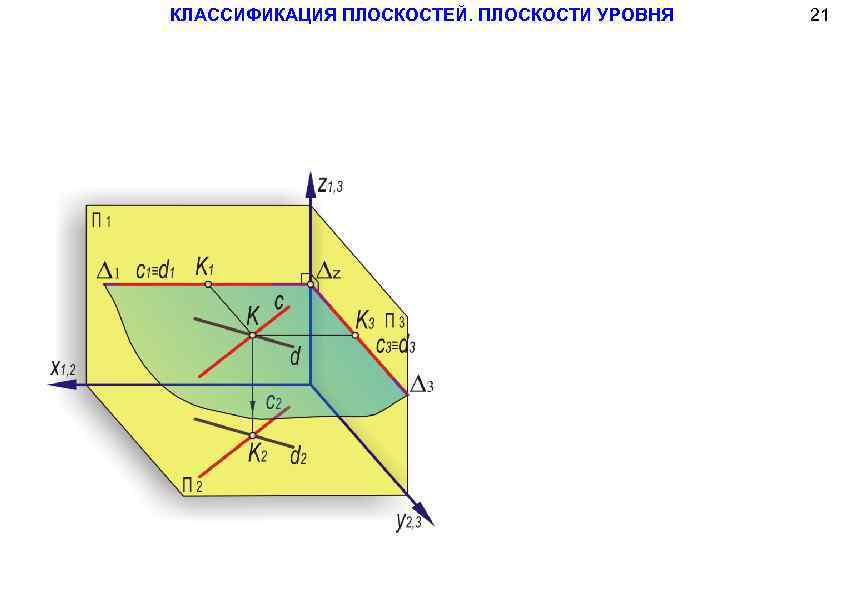 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 21
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 21
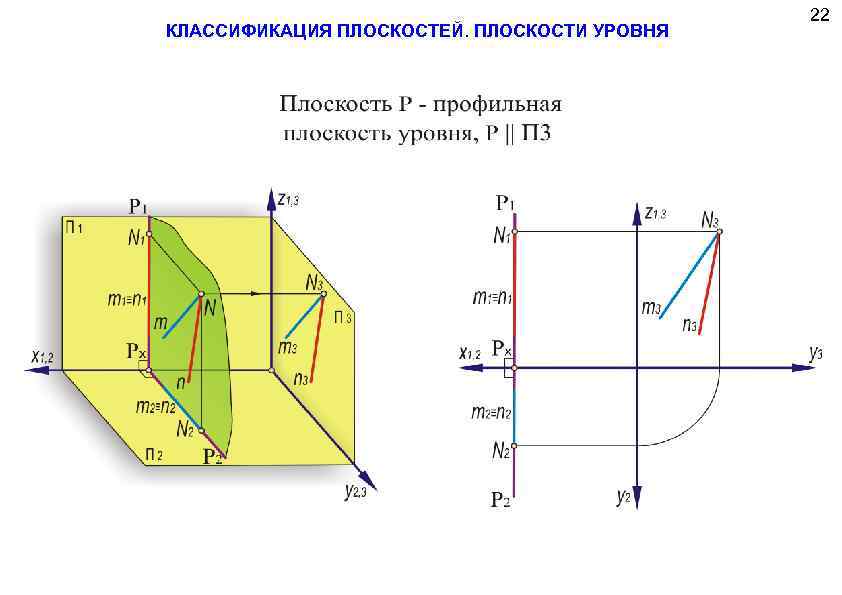 КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 22
КЛАССИФИКАЦИЯ ПЛОСКОСТЕЙ. ПЛОСКОСТИ УРОВНЯ 22
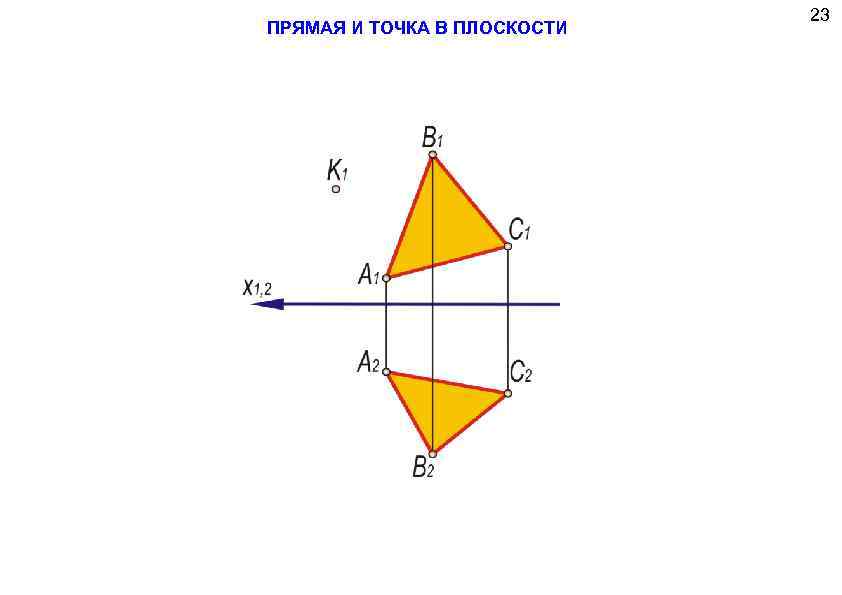 ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ 23
ПРЯМАЯ И ТОЧКА В ПЛОСКОСТИ 23
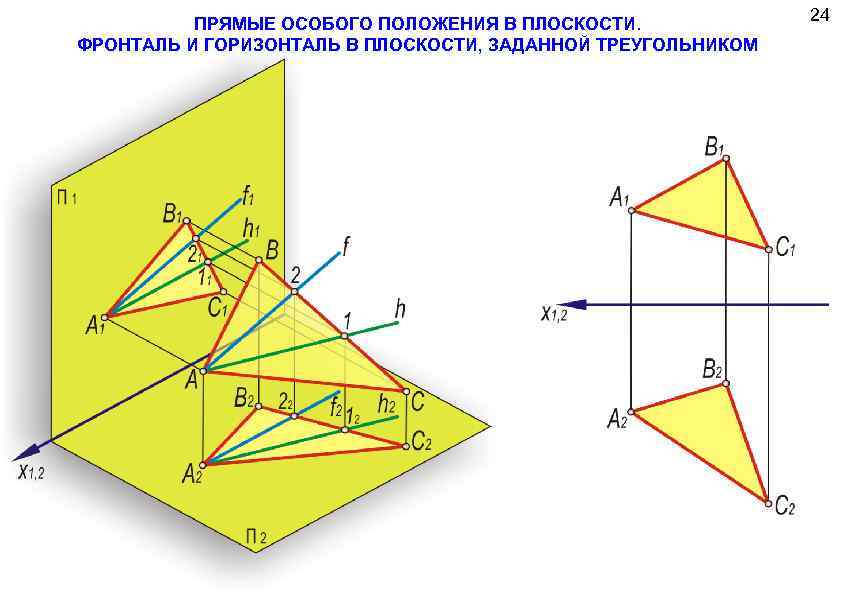 ПРЯМЫЕ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ. ФРОНТАЛЬ И ГОРИЗОНТАЛЬ В ПЛОСКОСТИ, ЗАДАННОЙ ТРЕУГОЛЬНИКОМ 24
ПРЯМЫЕ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ. ФРОНТАЛЬ И ГОРИЗОНТАЛЬ В ПЛОСКОСТИ, ЗАДАННОЙ ТРЕУГОЛЬНИКОМ 24
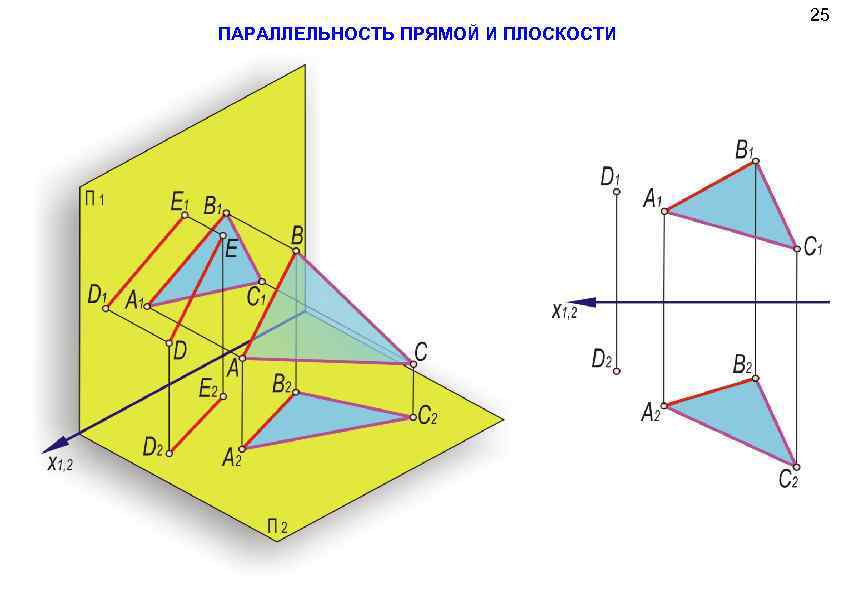 ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ 25
ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ 25
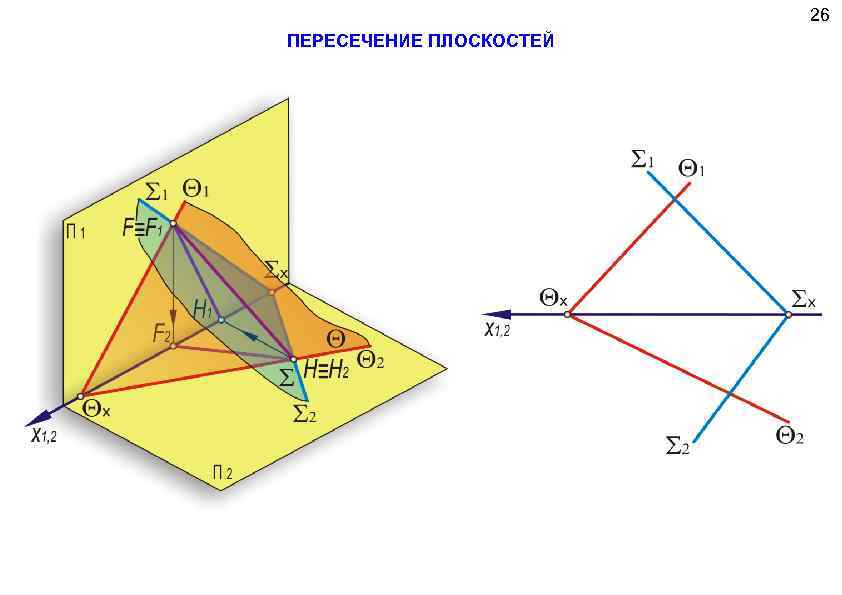 26 ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
26 ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
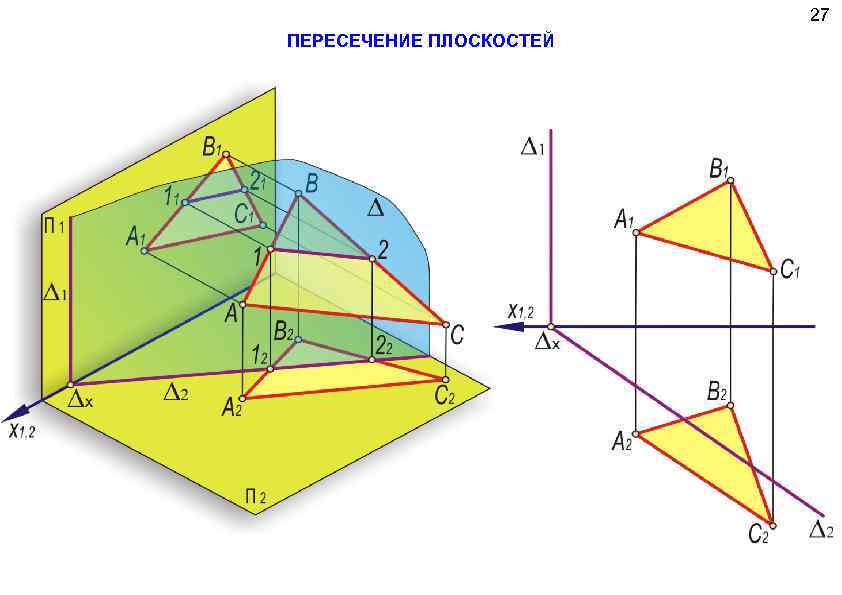 27 ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
27 ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ
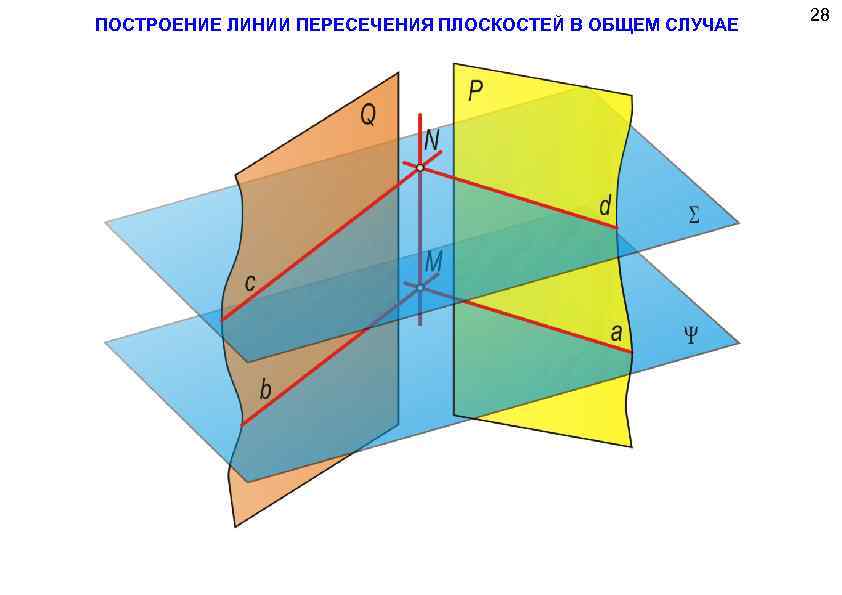 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ В ОБЩЕМ СЛУЧАЕ 28
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ В ОБЩЕМ СЛУЧАЕ 28
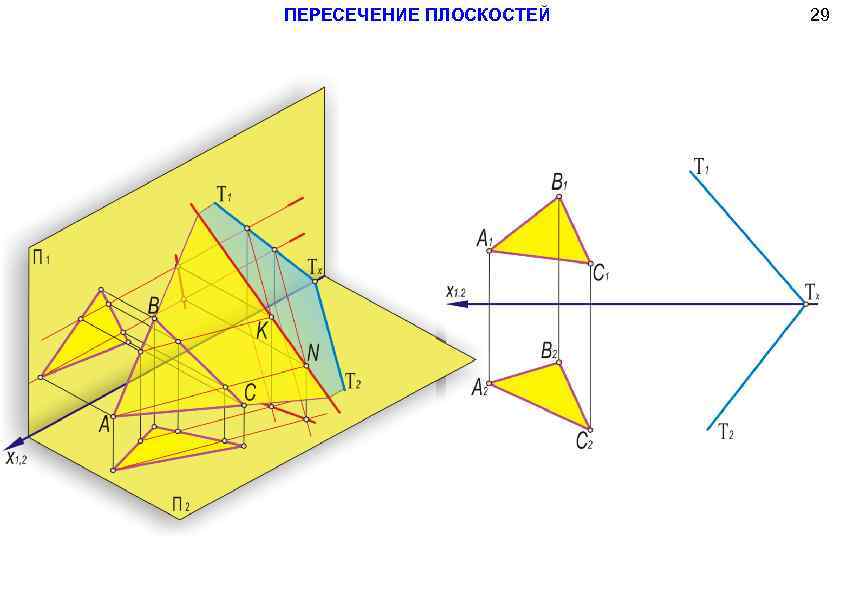 ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ 29
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ 29
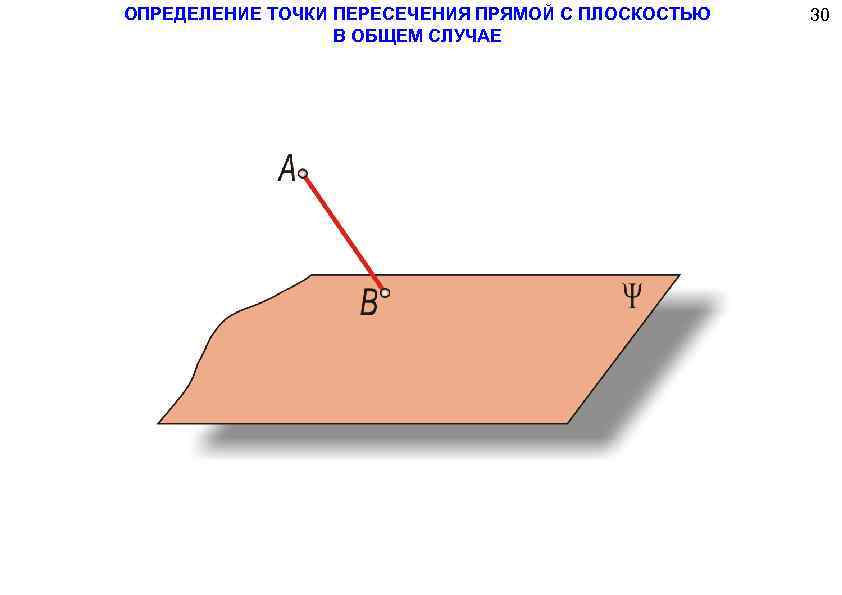 ОПРЕДЕЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ В ОБЩЕМ СЛУЧАЕ 30
ОПРЕДЕЛЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ В ОБЩЕМ СЛУЧАЕ 30
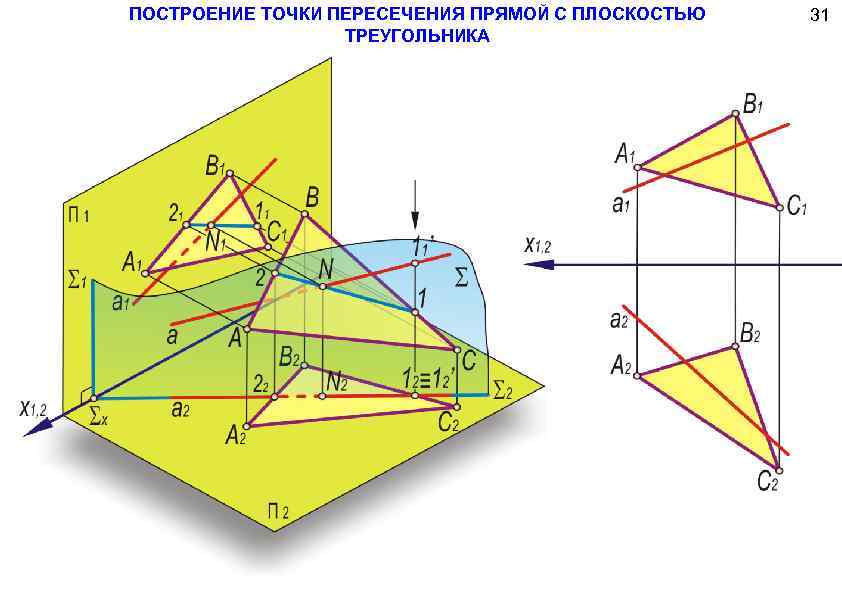 ПОСТРОЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ ТРЕУГОЛЬНИКА 31
ПОСТРОЕНИЕ ТОЧКИ ПЕРЕСЕЧЕНИЯ ПРЯМОЙ С ПЛОСКОСТЬЮ ТРЕУГОЛЬНИКА 31
 СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА ВРАЩЕНИЕ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ОСИ 32
СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА ВРАЩЕНИЕ ВОКРУГ ПРОЕЦИРУЮЩЕЙ ОСИ 32
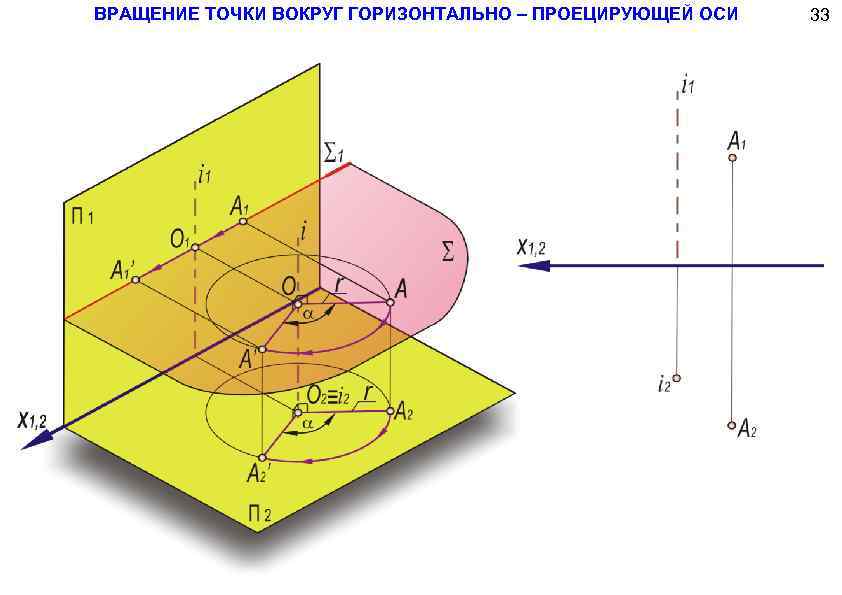 ВРАЩЕНИЕ ТОЧКИ ВОКРУГ ГОРИЗОНТАЛЬНО – ПРОЕЦИРУЮЩЕЙ ОСИ 33
ВРАЩЕНИЕ ТОЧКИ ВОКРУГ ГОРИЗОНТАЛЬНО – ПРОЕЦИРУЮЩЕЙ ОСИ 33
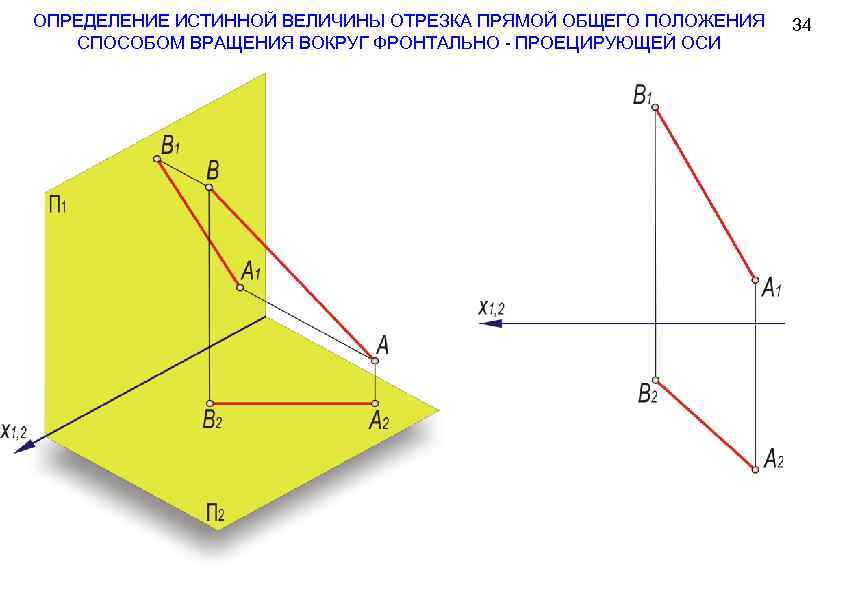 ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ СПОСОБОМ ВРАЩЕНИЯ ВОКРУГ ФРОНТАЛЬНО - ПРОЕЦИРУЮЩЕЙ ОСИ 34
ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ СПОСОБОМ ВРАЩЕНИЯ ВОКРУГ ФРОНТАЛЬНО - ПРОЕЦИРУЮЩЕЙ ОСИ 34
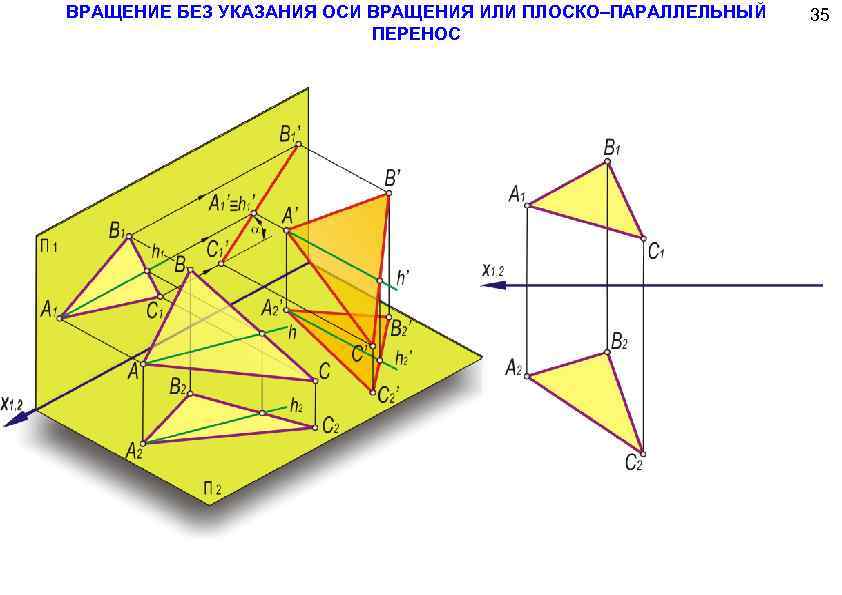 ВРАЩЕНИЕ БЕЗ УКАЗАНИЯ ОСИ ВРАЩЕНИЯ ИЛИ ПЛОСКО–ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС 35
ВРАЩЕНИЕ БЕЗ УКАЗАНИЯ ОСИ ВРАЩЕНИЯ ИЛИ ПЛОСКО–ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС 35
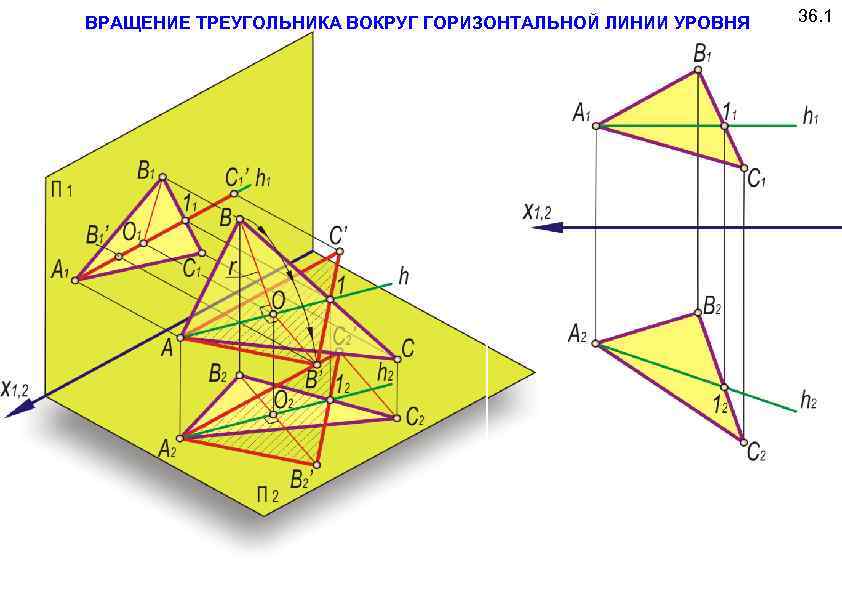 ВРАЩЕНИЕ ТРЕУГОЛЬНИКА ВОКРУГ ГОРИЗОНТАЛЬНОЙ ЛИНИИ УРОВНЯ 36. 1
ВРАЩЕНИЕ ТРЕУГОЛЬНИКА ВОКРУГ ГОРИЗОНТАЛЬНОЙ ЛИНИИ УРОВНЯ 36. 1
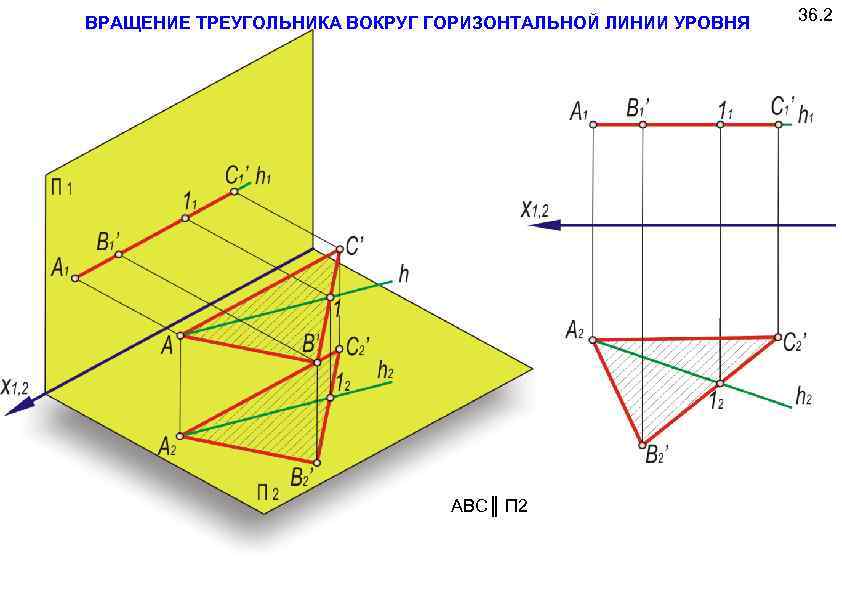 ВРАЩЕНИЕ ТРЕУГОЛЬНИКА ВОКРУГ ГОРИЗОНТАЛЬНОЙ ЛИНИИ УРОВНЯ АВС║ П 2 36. 2
ВРАЩЕНИЕ ТРЕУГОЛЬНИКА ВОКРУГ ГОРИЗОНТАЛЬНОЙ ЛИНИИ УРОВНЯ АВС║ П 2 36. 2
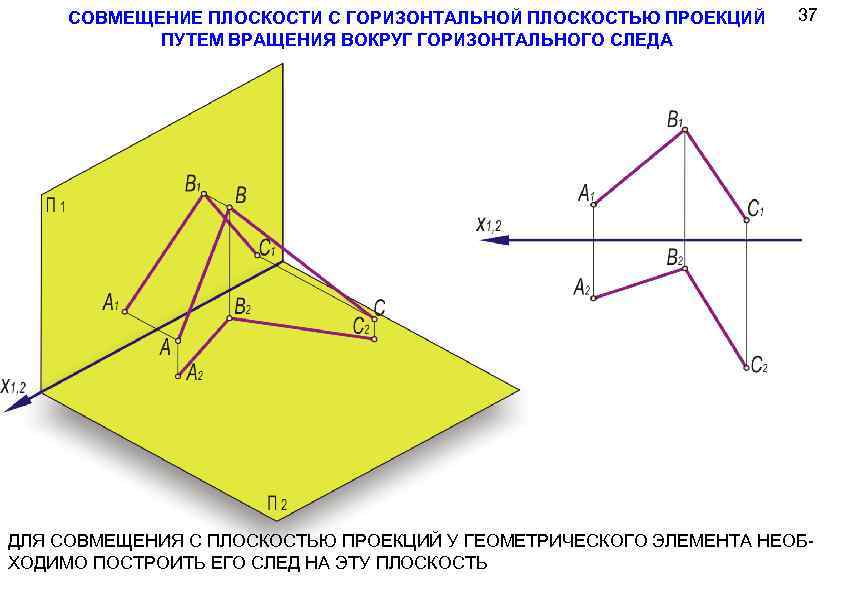 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА 37 ДЛЯ СОВМЕЩЕНИЯ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ У ГЕОМЕТРИЧЕСКОГО ЭЛЕМЕНТА НЕОБХОДИМО ПОСТРОИТЬ ЕГО СЛЕД НА ЭТУ ПЛОСКОСТЬ
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА 37 ДЛЯ СОВМЕЩЕНИЯ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ У ГЕОМЕТРИЧЕСКОГО ЭЛЕМЕНТА НЕОБХОДИМО ПОСТРОИТЬ ЕГО СЛЕД НА ЭТУ ПЛОСКОСТЬ
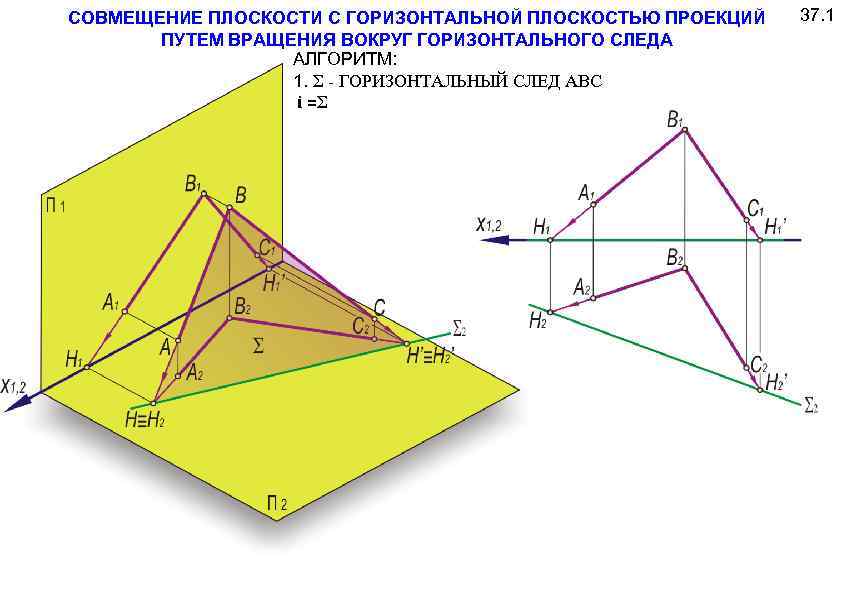 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 37. 1
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 37. 1
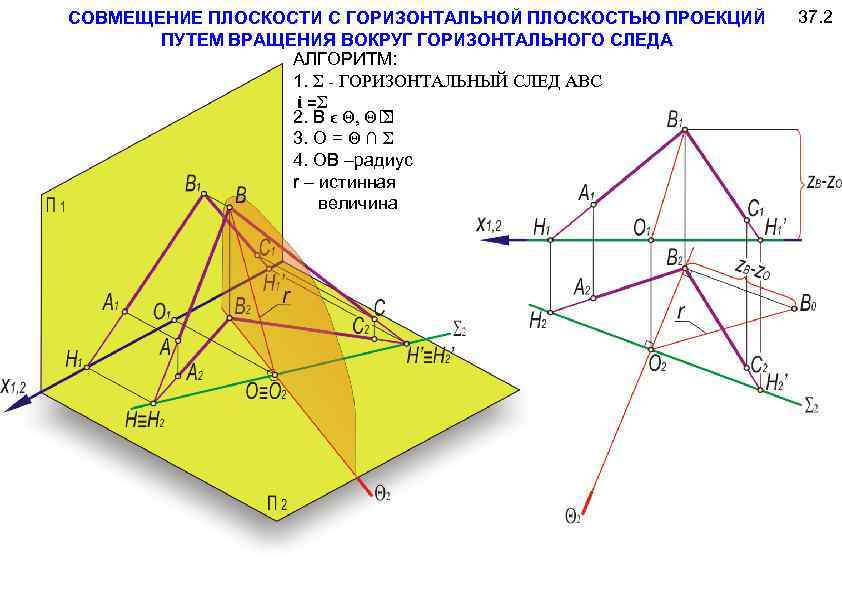 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 2. В ϵ Θ, Θ Σ 3. О = Θ ∩ Σ 4. ОВ –радиус r – истинная величина 37. 2
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 2. В ϵ Θ, Θ Σ 3. О = Θ ∩ Σ 4. ОВ –радиус r – истинная величина 37. 2
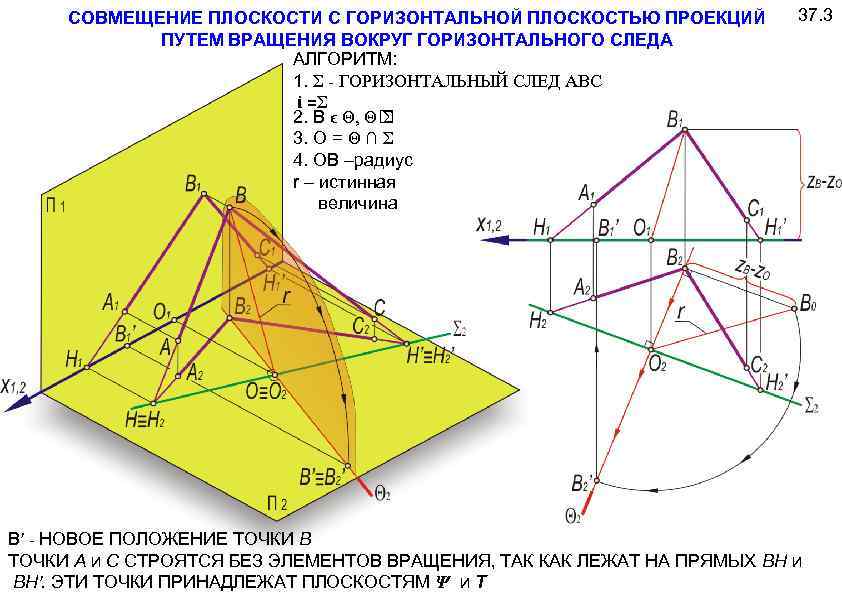 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 2. В ϵ Θ, Θ Σ 3. О = Θ ∩ Σ 4. ОВ –радиус r – истинная величина 37. 3 В′ - НОВОЕ ПОЛОЖЕНИЕ ТОЧКИ В ТОЧКИ А И С СТРОЯТСЯ БЕЗ ЭЛЕМЕНТОВ ВРАЩЕНИЯ, ТАК КАК ЛЕЖАТ НА ПРЯМЫХ BH И BH′. ЭТИ ТОЧКИ ПРИНАДЛЕЖАТ ПЛОСКОСТЯМ Ψ И Т
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА АЛГОРИТМ: 1. Σ - ГОРИЗОНТАЛЬНЫЙ СЛЕД АВС i =Σ 2. В ϵ Θ, Θ Σ 3. О = Θ ∩ Σ 4. ОВ –радиус r – истинная величина 37. 3 В′ - НОВОЕ ПОЛОЖЕНИЕ ТОЧКИ В ТОЧКИ А И С СТРОЯТСЯ БЕЗ ЭЛЕМЕНТОВ ВРАЩЕНИЯ, ТАК КАК ЛЕЖАТ НА ПРЯМЫХ BH И BH′. ЭТИ ТОЧКИ ПРИНАДЛЕЖАТ ПЛОСКОСТЯМ Ψ И Т
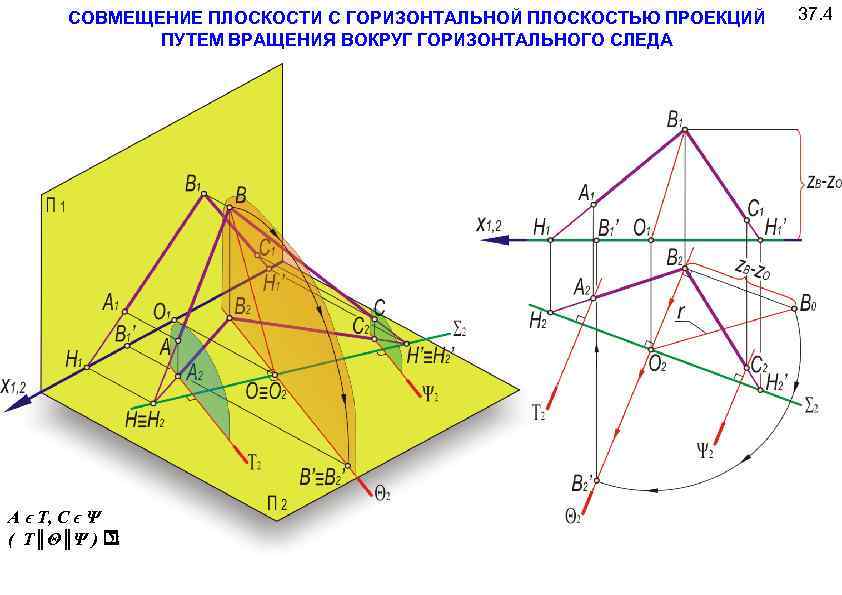 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА А ϵ Т, С ϵ Ψ ( Т║Θ║Ψ ) Σ 37. 4
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА А ϵ Т, С ϵ Ψ ( Т║Θ║Ψ ) Σ 37. 4
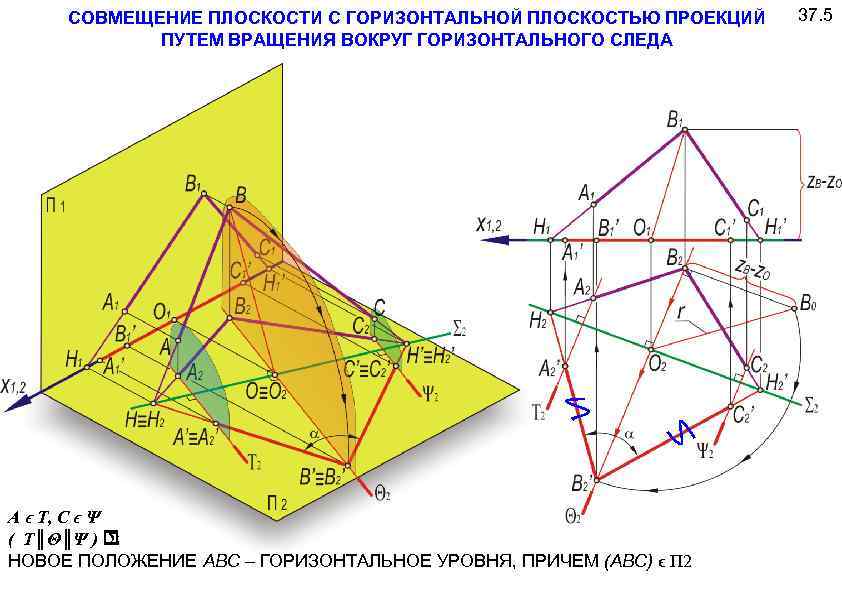 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА А ϵ Т, С ϵ Ψ ( Т║Θ║Ψ ) Σ НОВОЕ ПОЛОЖЕНИЕ АВС – ГОРИЗОНТАЛЬНОЕ УРОВНЯ, ПРИЧЕМ (АВС) ϵ П 2 37. 5
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА А ϵ Т, С ϵ Ψ ( Т║Θ║Ψ ) Σ НОВОЕ ПОЛОЖЕНИЕ АВС – ГОРИЗОНТАЛЬНОЕ УРОВНЯ, ПРИЧЕМ (АВС) ϵ П 2 37. 5
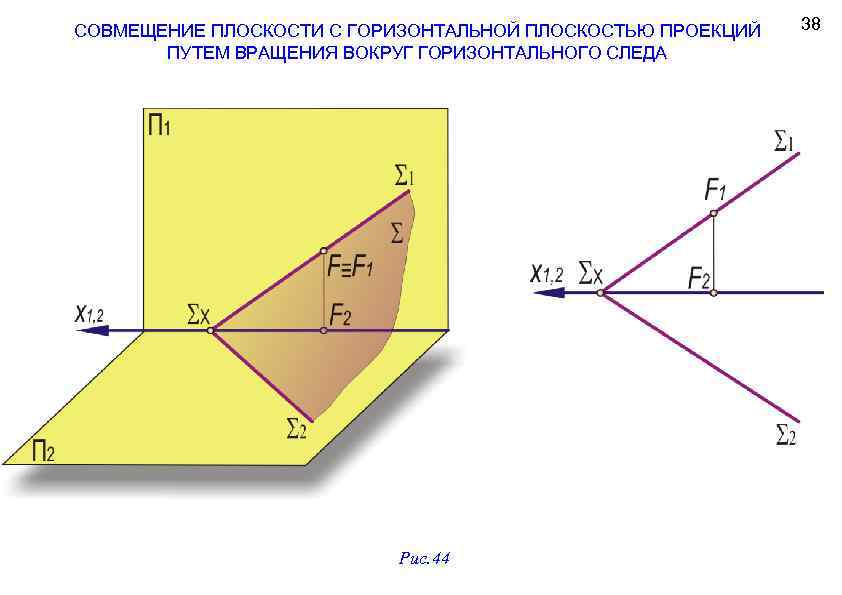 СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА Рис. 44 38
СОВМЕЩЕНИЕ ПЛОСКОСТИ С ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТЬЮ ПРОЕКЦИЙ ПУТЕМ ВРАЩЕНИЯ ВОКРУГ ГОРИЗОНТАЛЬНОГО СЛЕДА Рис. 44 38
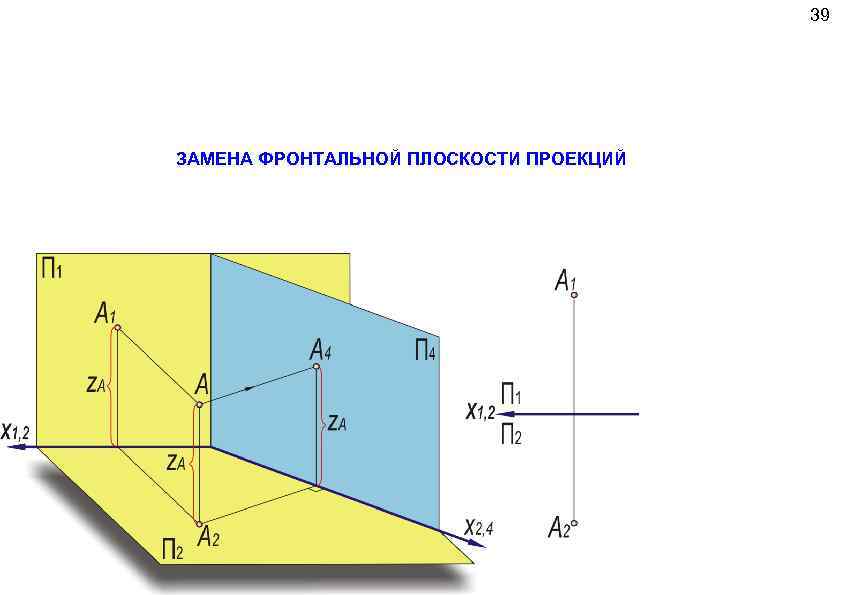 39 ЗАМЕНА ФРОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ
39 ЗАМЕНА ФРОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ
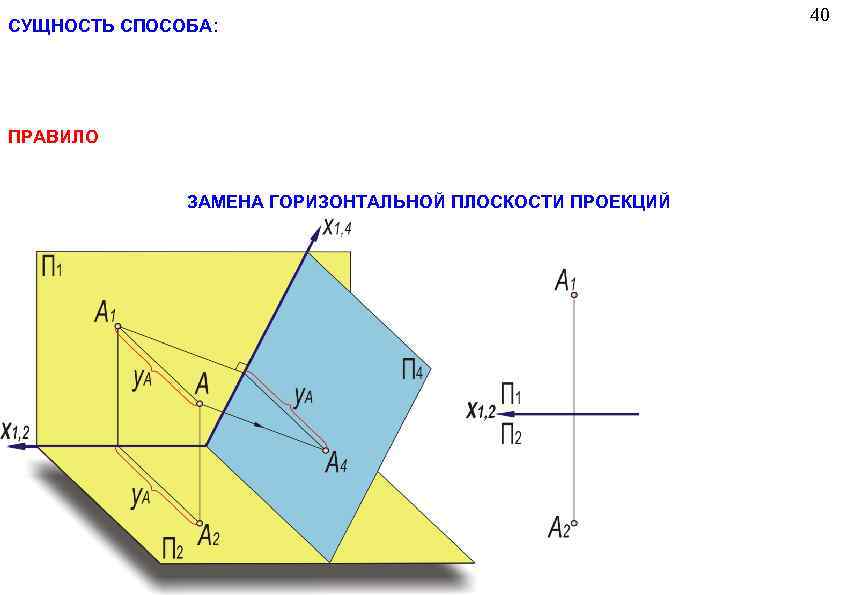 СУЩНОСТЬ СПОСОБА: ПРАВИЛО ЗАМЕНА ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ 40
СУЩНОСТЬ СПОСОБА: ПРАВИЛО ЗАМЕНА ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ 40
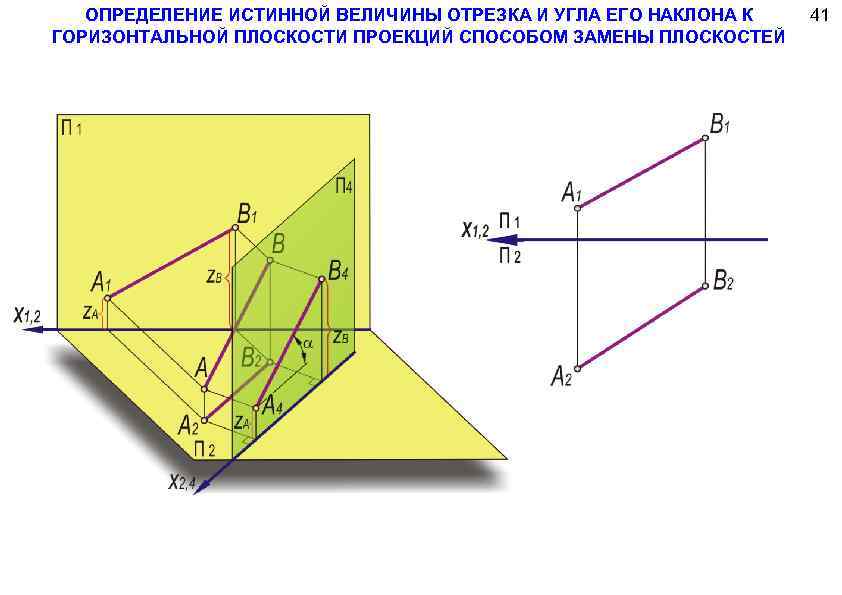 ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА И УГЛА ЕГО НАКЛОНА К ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ 41
ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ ОТРЕЗКА И УГЛА ЕГО НАКЛОНА К ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ 41
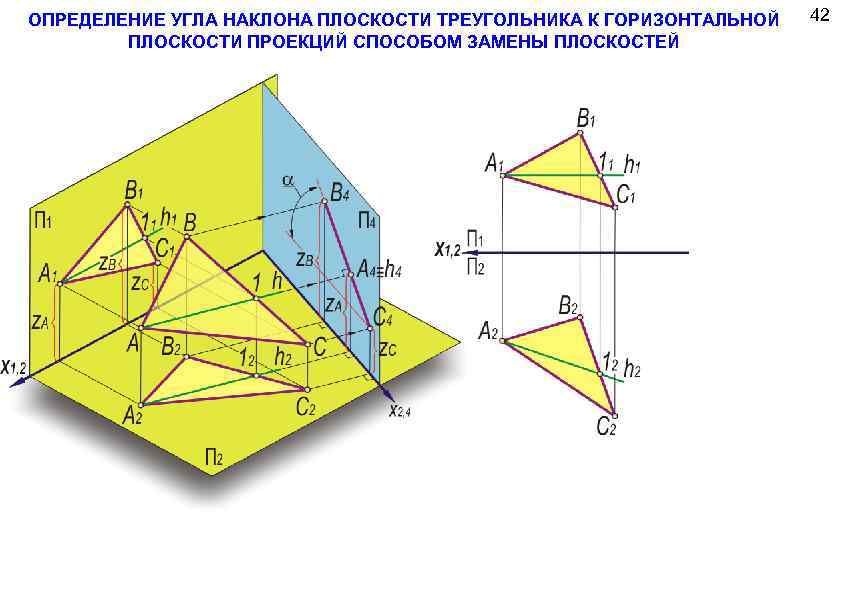 ОПРЕДЕЛЕНИЕ УГЛА НАКЛОНА ПЛОСКОСТИ ТРЕУГОЛЬНИКА К ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ 42
ОПРЕДЕЛЕНИЕ УГЛА НАКЛОНА ПЛОСКОСТИ ТРЕУГОЛЬНИКА К ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРОЕКЦИЙ СПОСОБОМ ЗАМЕНЫ ПЛОСКОСТЕЙ 42
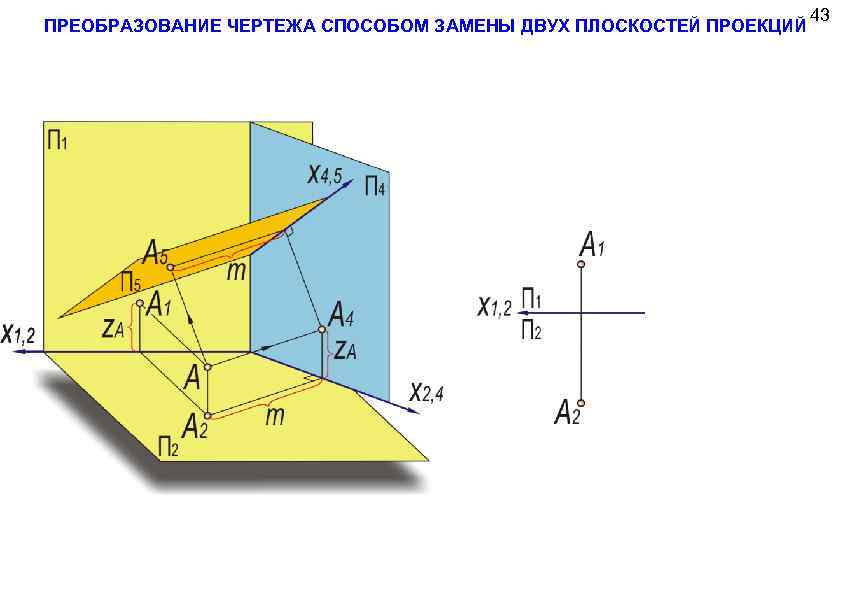 ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА СПОСОБОМ ЗАМЕНЫ ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 43
ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА СПОСОБОМ ЗАМЕНЫ ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 43
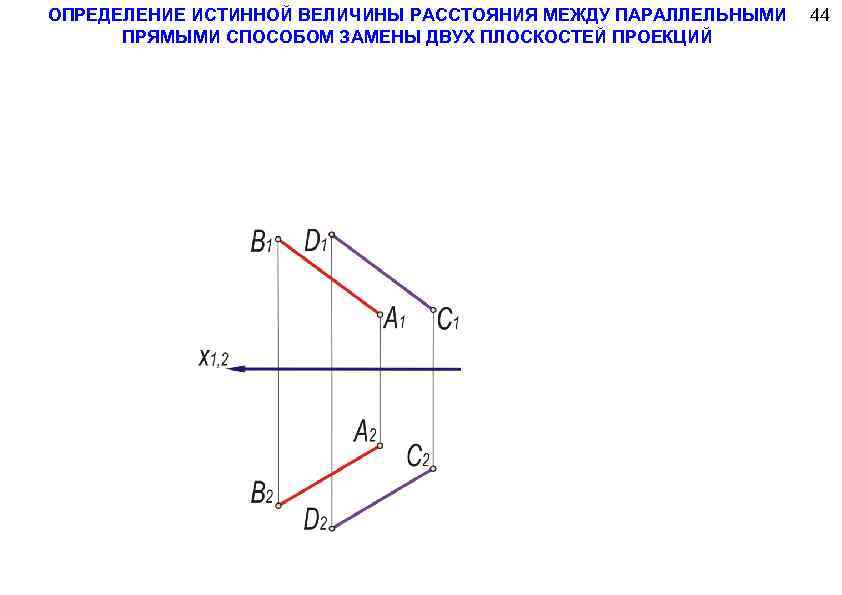 ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ РАССТОЯНИЯ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ СПОСОБОМ ЗАМЕНЫ ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 44
ОПРЕДЕЛЕНИЕ ИСТИННОЙ ВЕЛИЧИНЫ РАССТОЯНИЯ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ СПОСОБОМ ЗАМЕНЫ ДВУХ ПЛОСКОСТЕЙ ПРОЕКЦИЙ 44
 ПОВЕРХНОСТИ В НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ПОВЕРХНОСТИ РАССМАТРИВАЮТ С ТОЧКИ ЗРЕНИЯ СПОСОБА ОБРАЗОВАНИЯ: НА ЭПЮРЕ МОНЖА ПОВЕРХНОСТЬ ЗАДАЕТСЯ: КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ЛИНЕЙЧАТЫЕ 45
ПОВЕРХНОСТИ В НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ ПОВЕРХНОСТИ РАССМАТРИВАЮТ С ТОЧКИ ЗРЕНИЯ СПОСОБА ОБРАЗОВАНИЯ: НА ЭПЮРЕ МОНЖА ПОВЕРХНОСТЬ ЗАДАЕТСЯ: КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ ЛИНЕЙЧАТЫЕ 45
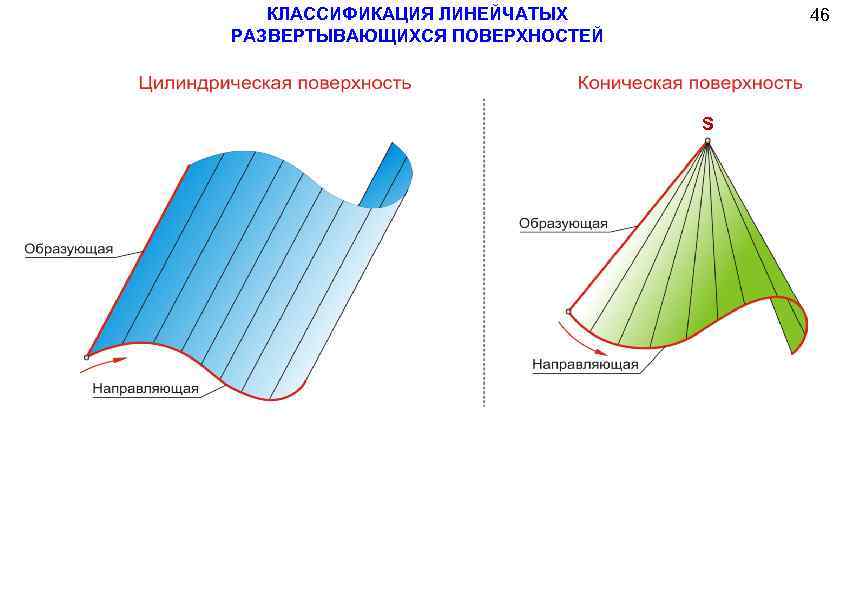 КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ 46 S
КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ 46 S
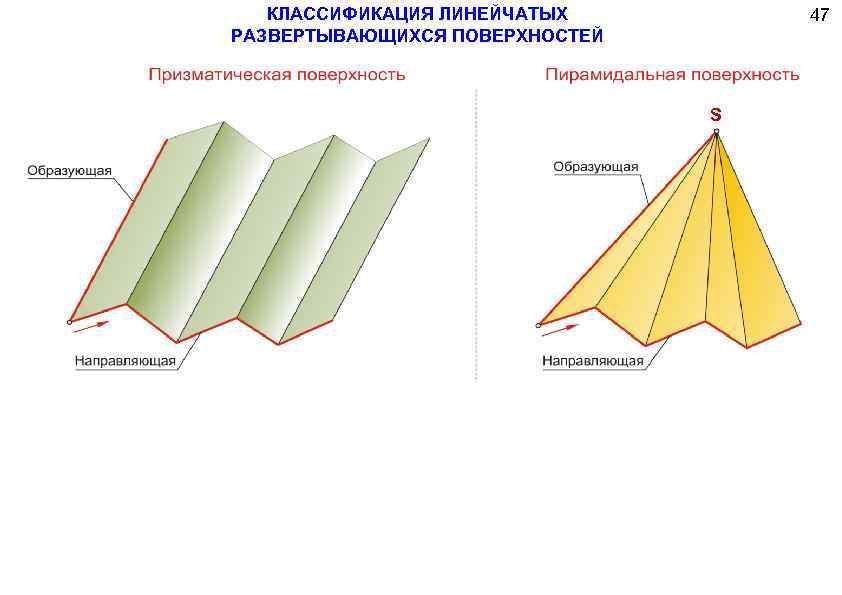 КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ 47 S
КЛАССИФИКАЦИЯ ЛИНЕЙЧАТЫХ РАЗВЕРТЫВАЮЩИХСЯ ПОВЕРХНОСТЕЙ 47 S
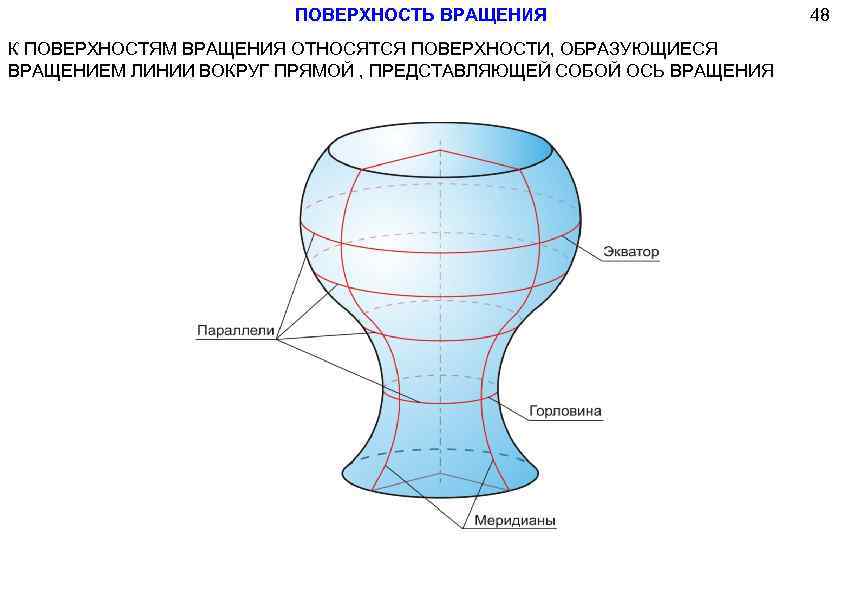 ПОВЕРХНОСТЬ ВРАЩЕНИЯ К ПОВЕРХНОСТЯМ ВРАЩЕНИЯ ОТНОСЯТСЯ ПОВЕРХНОСТИ, ОБРАЗУЮЩИЕСЯ ВРАЩЕНИЕМ ЛИНИИ ВОКРУГ ПРЯМОЙ , ПРЕДСТАВЛЯЮЩЕЙ СОБОЙ ОСЬ ВРАЩЕНИЯ 48
ПОВЕРХНОСТЬ ВРАЩЕНИЯ К ПОВЕРХНОСТЯМ ВРАЩЕНИЯ ОТНОСЯТСЯ ПОВЕРХНОСТИ, ОБРАЗУЮЩИЕСЯ ВРАЩЕНИЕМ ЛИНИИ ВОКРУГ ПРЯМОЙ , ПРЕДСТАВЛЯЮЩЕЙ СОБОЙ ОСЬ ВРАЩЕНИЯ 48
 ЗАДАНИЕ ПОВЕРХНОСТИ 49 ПОВЕРХНОСТИ РАССМАТРИВАЮТСЯ С ТОЧКИ ЗРЕНИЯ ИХ КИНЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ, КАК СОВОКУПНОСТЬ ПОСЛЕДОВАТЕЛЬНЫХ ДВИЖЕНИЙ ОБРАЗУЮЩЕЙ ПО НЕПОДВИЖНОЙ НАПРАВЛЯЮЩЕЙ ДРУГИМ СПОСОБОМ ЗАДАНИЯ ПОВЕРХНОСТИ ЯВЛЯЕТСЯ ЗАДАНИЕ КАРКАСА – МНОЖЕСТВА ТОЧЕК ИЛИ ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТИ ПОВЕРХНОСТЬ СЧИТАЕТСЯ ЗАДАННОЙ НА ЧЕРТЕЖЕ, ЕСЛИ ПО ОДНОЙ ПРОЕКЦИИ ТОЧКИ, ПРИНАДЛЕЖАЩЕЙ ПОВЕРХНОСТИ, МОЖНО ПОСТРОИТЬ ДРУГУЮ СЕЧЕНИЕ ПОВЕРХНОСТИ СФЕРЫ ПЛОСКОСТЬЮ
ЗАДАНИЕ ПОВЕРХНОСТИ 49 ПОВЕРХНОСТИ РАССМАТРИВАЮТСЯ С ТОЧКИ ЗРЕНИЯ ИХ КИНЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ, КАК СОВОКУПНОСТЬ ПОСЛЕДОВАТЕЛЬНЫХ ДВИЖЕНИЙ ОБРАЗУЮЩЕЙ ПО НЕПОДВИЖНОЙ НАПРАВЛЯЮЩЕЙ ДРУГИМ СПОСОБОМ ЗАДАНИЯ ПОВЕРХНОСТИ ЯВЛЯЕТСЯ ЗАДАНИЕ КАРКАСА – МНОЖЕСТВА ТОЧЕК ИЛИ ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТИ ПОВЕРХНОСТЬ СЧИТАЕТСЯ ЗАДАННОЙ НА ЧЕРТЕЖЕ, ЕСЛИ ПО ОДНОЙ ПРОЕКЦИИ ТОЧКИ, ПРИНАДЛЕЖАЩЕЙ ПОВЕРХНОСТИ, МОЖНО ПОСТРОИТЬ ДРУГУЮ СЕЧЕНИЕ ПОВЕРХНОСТИ СФЕРЫ ПЛОСКОСТЬЮ
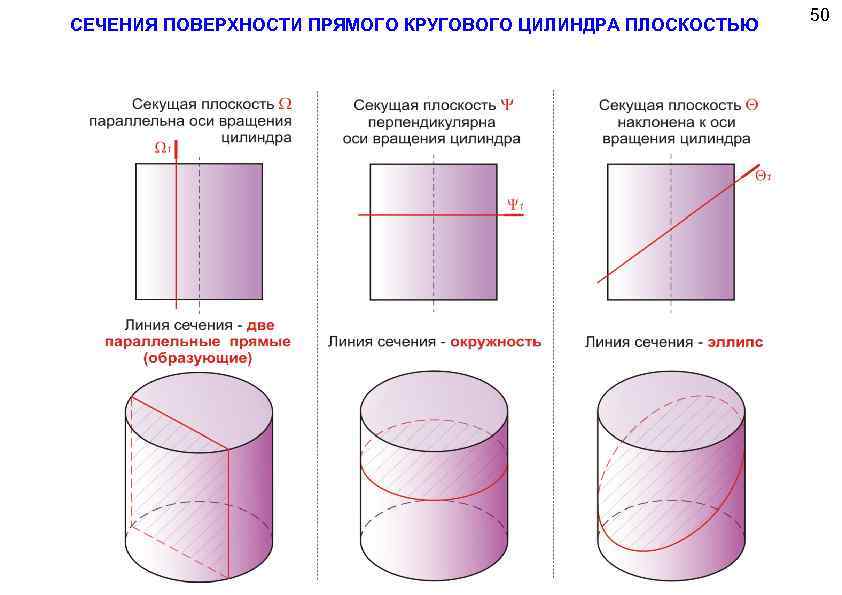 СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО ЦИЛИНДРА ПЛОСКОСТЬЮ 50
СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО ЦИЛИНДРА ПЛОСКОСТЬЮ 50
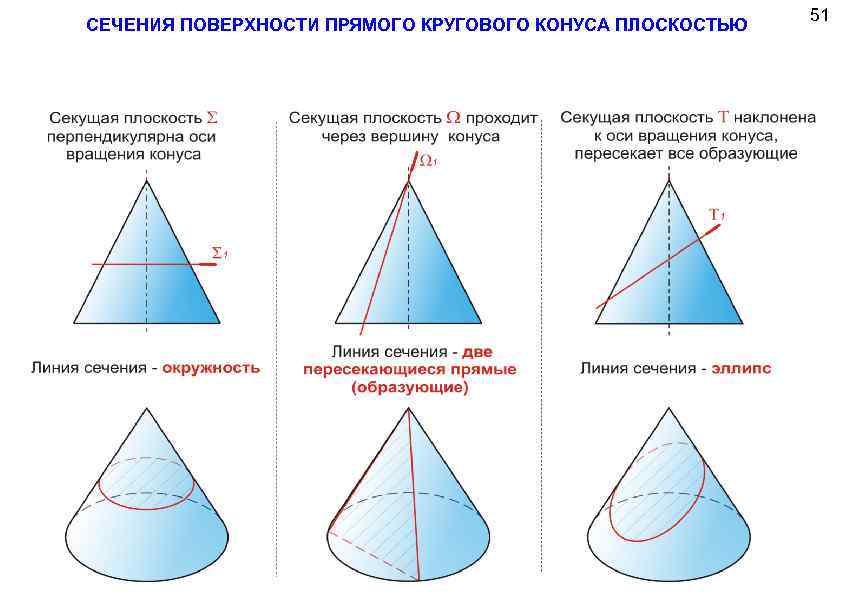 СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО КОНУСА ПЛОСКОСТЬЮ 51
СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО КОНУСА ПЛОСКОСТЬЮ 51
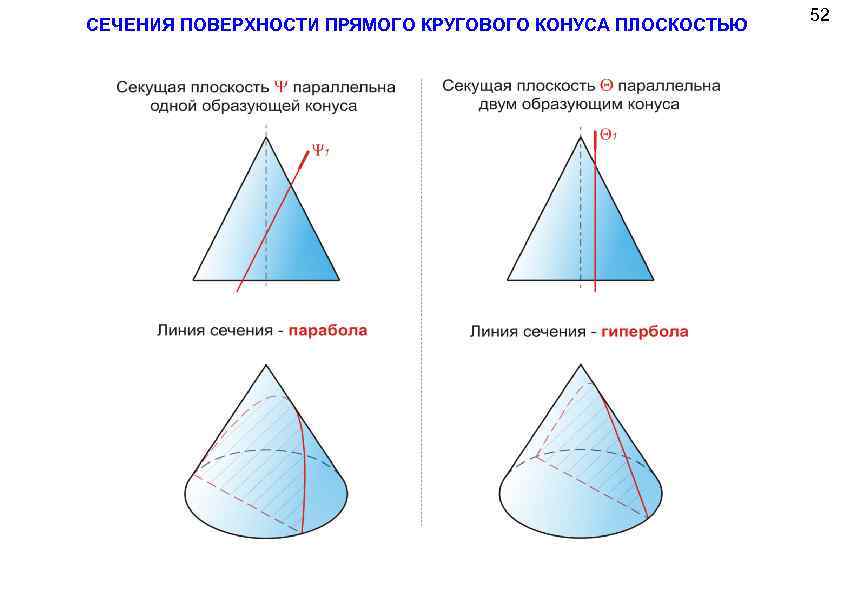 СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО КОНУСА ПЛОСКОСТЬЮ 52
СЕЧЕНИЯ ПОВЕРХНОСТИ ПРЯМОГО КРУГОВОГО КОНУСА ПЛОСКОСТЬЮ 52
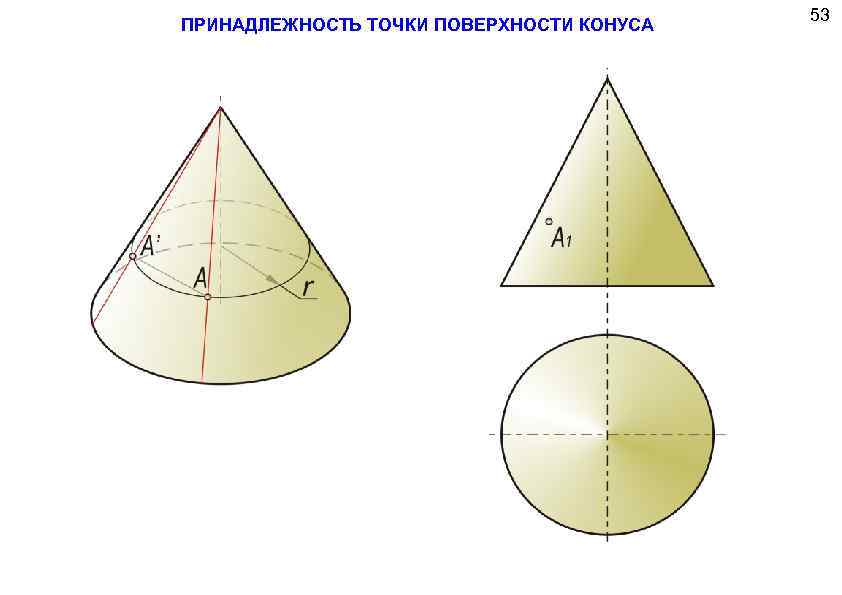 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ КОНУСА 53
ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ КОНУСА 53
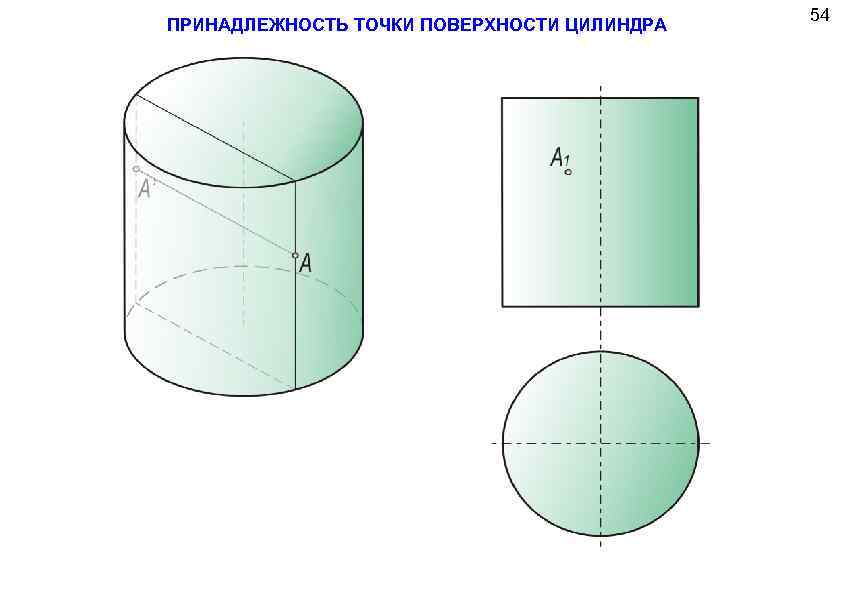 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ ЦИЛИНДРА 54
ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ ЦИЛИНДРА 54
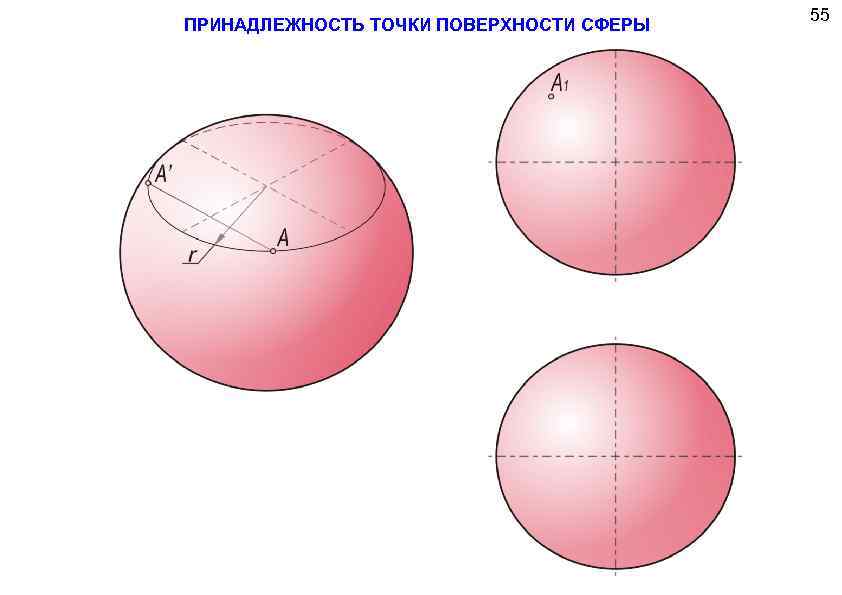 ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ СФЕРЫ 55
ПРИНАДЛЕЖНОСТЬ ТОЧКИ ПОВЕРХНОСТИ СФЕРЫ 55
 ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ (ПОСТРОЕНИЕ СЕЧЕНИЯ) ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ СПОСОБЫ ПОСТРОЕНИЯ: 1. СПОСОБ РЕБЕР. 2. СПОСОБ ГРАНЕЙ. 56
ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКА ПЛОСКОСТЬЮ (ПОСТРОЕНИЕ СЕЧЕНИЯ) ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ СПОСОБЫ ПОСТРОЕНИЯ: 1. СПОСОБ РЕБЕР. 2. СПОСОБ ГРАНЕЙ. 56
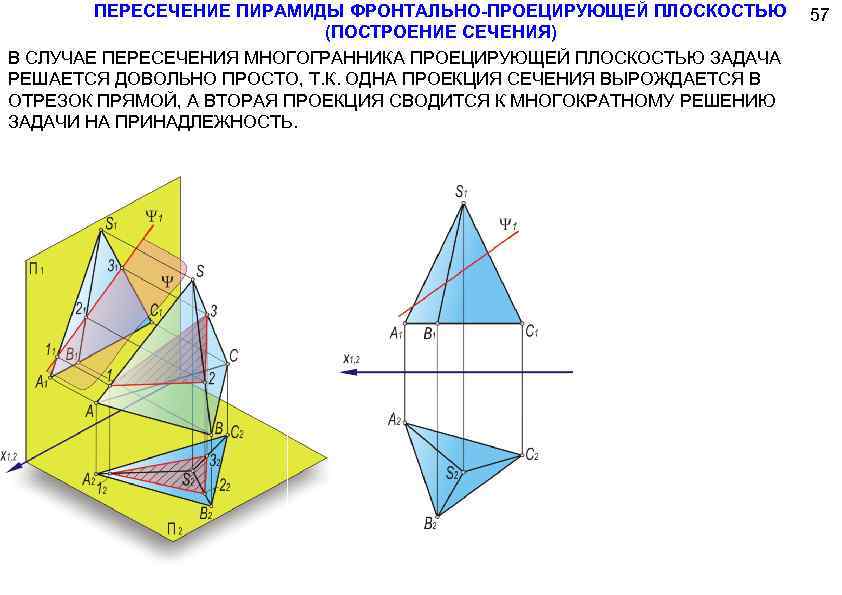 ПЕРЕСЕЧЕНИЕ ПИРАМИДЫ ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ (ПОСТРОЕНИЕ СЕЧЕНИЯ) В СЛУЧАЕ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКА ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ ЗАДАЧА РЕШАЕТСЯ ДОВОЛЬНО ПРОСТО, Т. К. ОДНА ПРОЕКЦИЯ СЕЧЕНИЯ ВЫРОЖДАЕТСЯ В ОТРЕЗОК ПРЯМОЙ, А ВТОРАЯ ПРОЕКЦИЯ СВОДИТСЯ К МНОГОКРАТНОМУ РЕШЕНИЮ ЗАДАЧИ НА ПРИНАДЛЕЖНОСТЬ. 57
ПЕРЕСЕЧЕНИЕ ПИРАМИДЫ ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ (ПОСТРОЕНИЕ СЕЧЕНИЯ) В СЛУЧАЕ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКА ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ ЗАДАЧА РЕШАЕТСЯ ДОВОЛЬНО ПРОСТО, Т. К. ОДНА ПРОЕКЦИЯ СЕЧЕНИЯ ВЫРОЖДАЕТСЯ В ОТРЕЗОК ПРЯМОЙ, А ВТОРАЯ ПРОЕКЦИЯ СВОДИТСЯ К МНОГОКРАТНОМУ РЕШЕНИЮ ЗАДАЧИ НА ПРИНАДЛЕЖНОСТЬ. 57
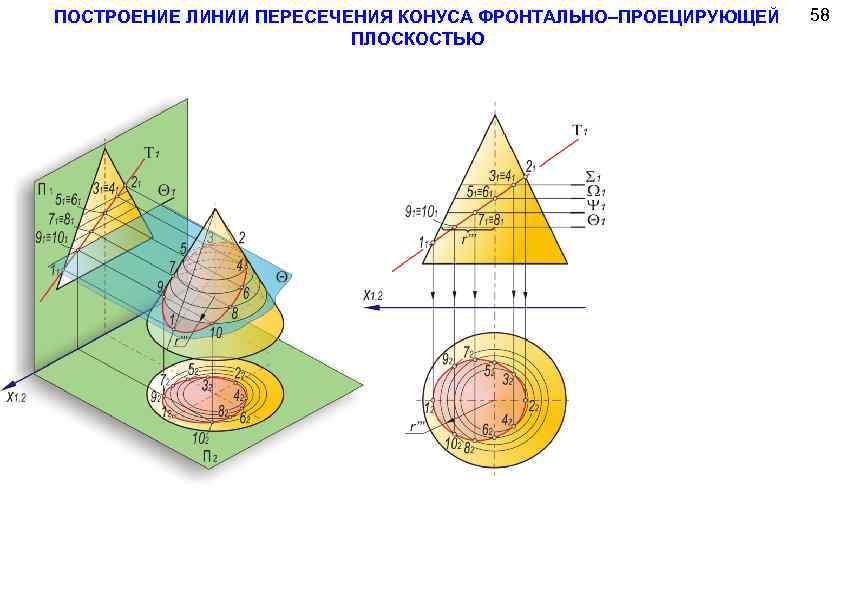 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ КОНУСА ФРОНТАЛЬНО–ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ 58
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ КОНУСА ФРОНТАЛЬНО–ПРОЕЦИРУЮЩЕЙ ПЛОСКОСТЬЮ 58
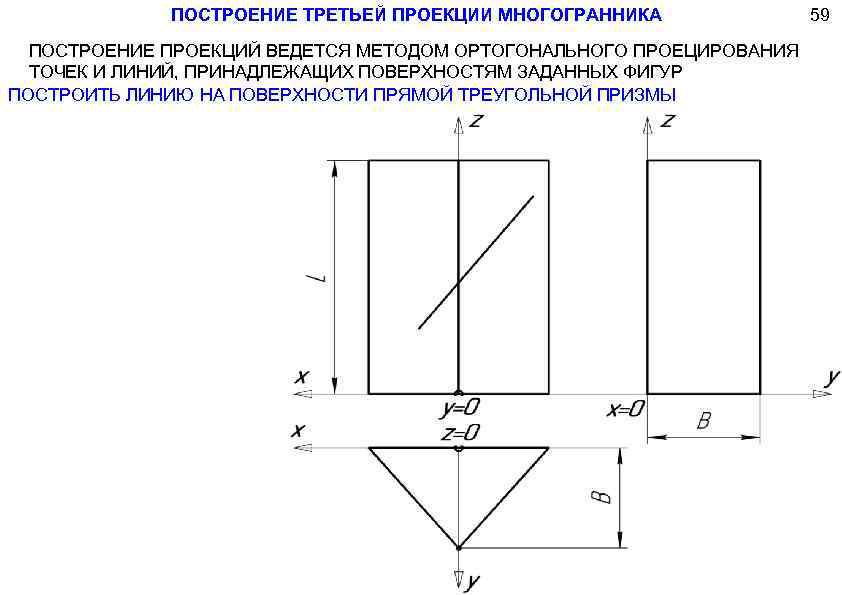 ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ МНОГОГРАННИКА ПОСТРОЕНИЕ ПРОЕКЦИЙ ВЕДЕТСЯ МЕТОДОМ ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ ТОЧЕК И ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТЯМ ЗАДАННЫХ ФИГУР ПОСТРОИТЬ ЛИНИЮ НА ПОВЕРХНОСТИ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ 59
ПОСТРОЕНИЕ ТРЕТЬЕЙ ПРОЕКЦИИ МНОГОГРАННИКА ПОСТРОЕНИЕ ПРОЕКЦИЙ ВЕДЕТСЯ МЕТОДОМ ОРТОГОНАЛЬНОГО ПРОЕЦИРОВАНИЯ ТОЧЕК И ЛИНИЙ, ПРИНАДЛЕЖАЩИХ ПОВЕРХНОСТЯМ ЗАДАННЫХ ФИГУР ПОСТРОИТЬ ЛИНИЮ НА ПОВЕРХНОСТИ ПРЯМОЙ ТРЕУГОЛЬНОЙ ПРИЗМЫ 59
 ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ С ПОВЕРХНОСТЬЮ ПИРАМИДЫ Рис. 57 60
ПОСТРОЕНИЕ ТОЧЕК ПЕРЕСЕЧЕНИЯ ФРОНТАЛЬНО-ПРОЕЦИРУЮЩЕЙ ПРЯМОЙ С ПОВЕРХНОСТЬЮ ПИРАМИДЫ Рис. 57 60
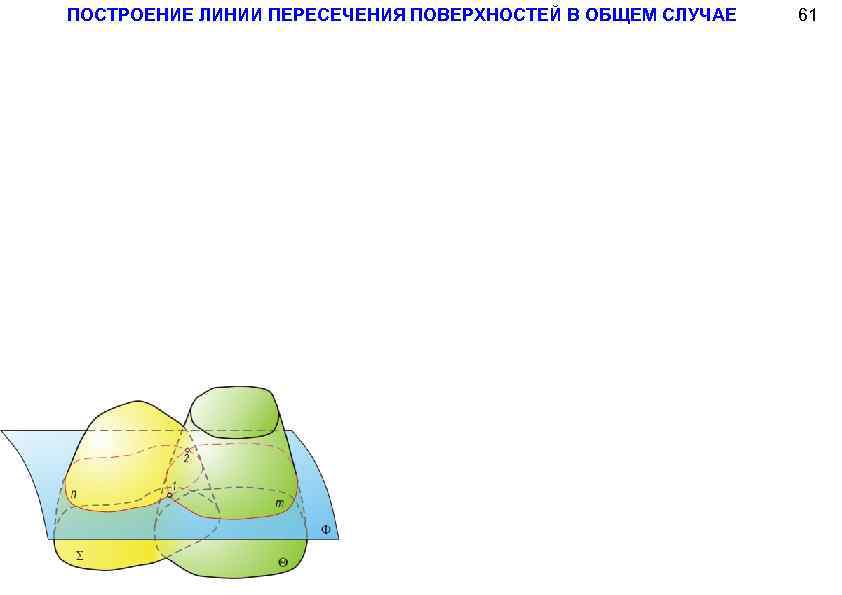 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ В ОБЩЕМ СЛУЧАЕ 61
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ В ОБЩЕМ СЛУЧАЕ 61
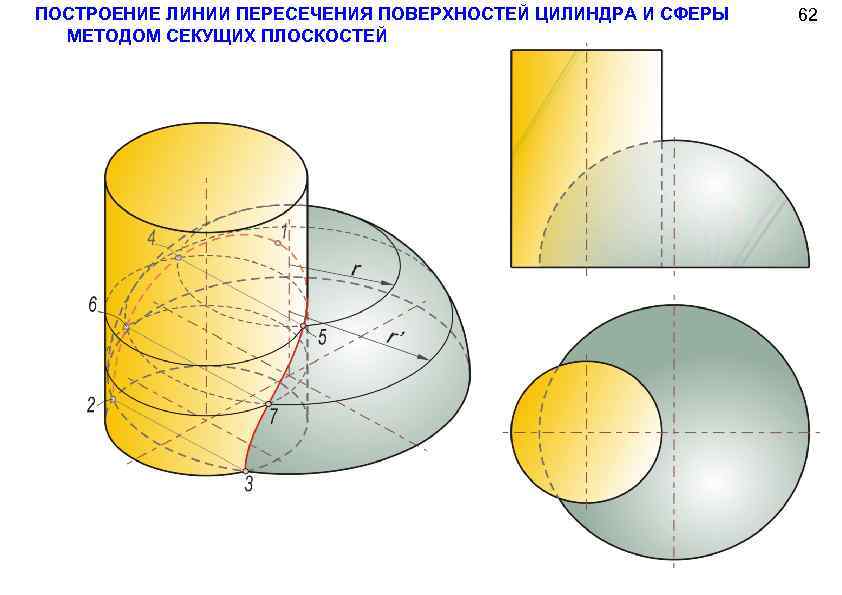 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И СФЕРЫ МЕТОДОМ СЕКУЩИХ ПЛОСКОСТЕЙ 62
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ ЦИЛИНДРА И СФЕРЫ МЕТОДОМ СЕКУЩИХ ПЛОСКОСТЕЙ 62
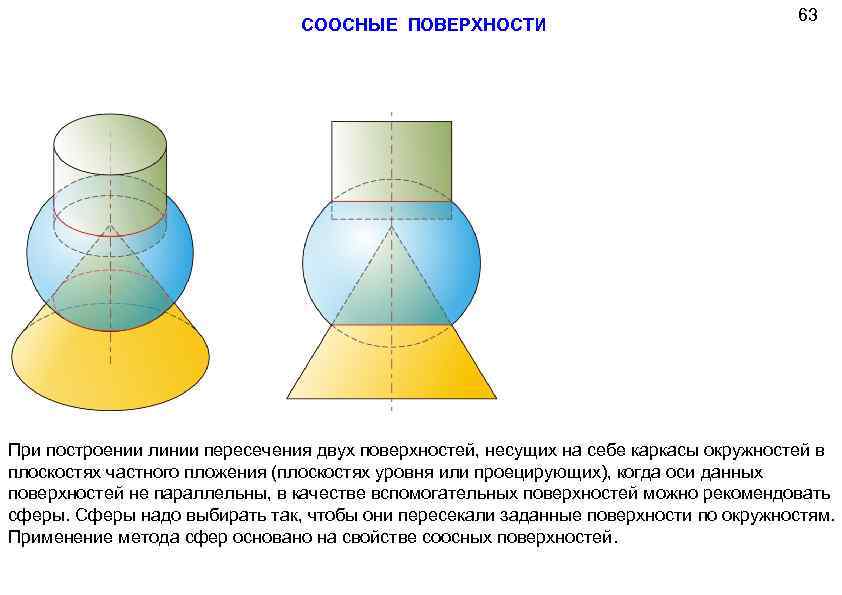 СООСНЫЕ ПОВЕРХНОСТИ 63 При построении линии пересечения двух поверхностей, несущих на себе каркасы окружностей в плоскостях частного пложения (плоскостях уровня или проецирующих), когда оси данных поверхностей не параллельны, в качестве вспомогательных поверхностей можно рекомендовать сферы. Сферы надо выбирать так, чтобы они пересекали заданные поверхности по окружностям. Применение метода сфер основано на свойстве соосных поверхностей.
СООСНЫЕ ПОВЕРХНОСТИ 63 При построении линии пересечения двух поверхностей, несущих на себе каркасы окружностей в плоскостях частного пложения (плоскостях уровня или проецирующих), когда оси данных поверхностей не параллельны, в качестве вспомогательных поверхностей можно рекомендовать сферы. Сферы надо выбирать так, чтобы они пересекали заданные поверхности по окружностям. Применение метода сфер основано на свойстве соосных поверхностей.
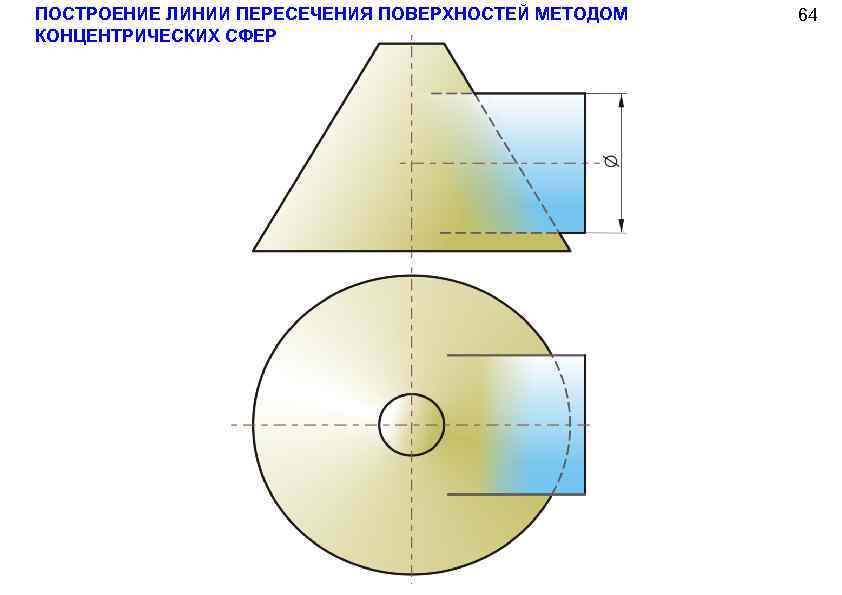 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ МЕТОДОМ КОНЦЕНТРИЧЕСКИХ СФЕР 64
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ МЕТОДОМ КОНЦЕНТРИЧЕСКИХ СФЕР 64
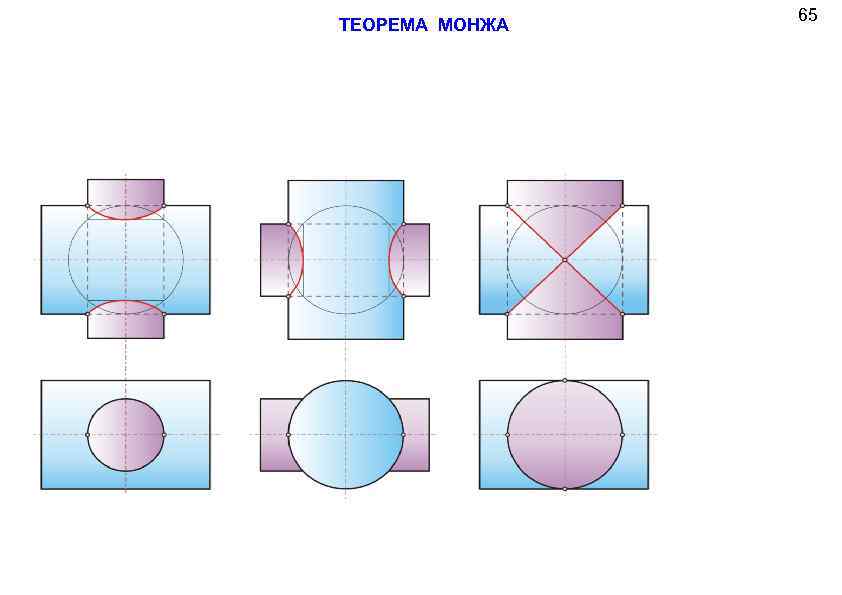 ТЕОРЕМА МОНЖА 65
ТЕОРЕМА МОНЖА 65
 ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ 2 СПОСОБА ПОСТРОЕНИЯ: 1. СПОСОБ РЕБЕР: 2. СПОСОБ ГРАНЕЙ: 66
ПЕРЕСЕЧЕНИЕ МНОГОГРАННИКОВ ЛИНИЕЙ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ 2 СПОСОБА ПОСТРОЕНИЯ: 1. СПОСОБ РЕБЕР: 2. СПОСОБ ГРАНЕЙ: 66
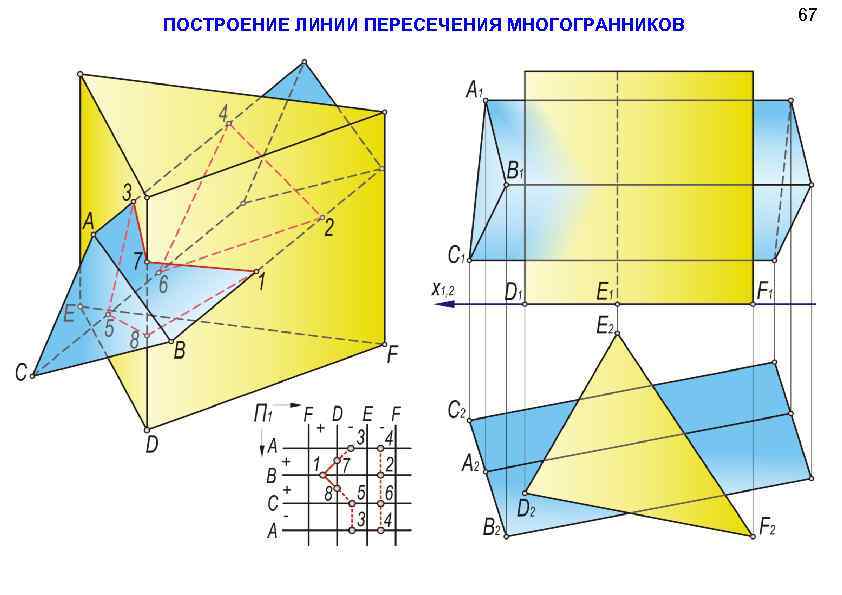 ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ 67
ПОСТРОЕНИЕ ЛИНИИ ПЕРЕСЕЧЕНИЯ МНОГОГРАННИКОВ 67


