Опорные знания 1 Центр описанной около треугольника окружности

Опорные знания 1. Центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров к сторонам треугольника. 2. Точка пересечения высот – ортоцентр. 3. Соединяя основания высот треугольника получимортотр еугольник.

Опорные знания 4. Теорема синусов : «Стороны треугольника пропорциональны синусам противолежащих углов. » 5. Вписанный угол, опирающийся на полуокружность, - прямой.

Педальный треугольник 1. Рассмотрим произвольный треугольник АВС. 2. Выберим любую точку Р внутри нашего треугольника. 3. Опустим перпендикуляры из точки Р на стороны АВ, ВС, АС. 4. Получаем РС 1, РВ 1, РА 1 5. Треугольник С 1 В 1 А 1 вершинами которого являются основания этих перпендикуляров, называется Педальным треугольником треугольника АВС для «педальной» точки Р.

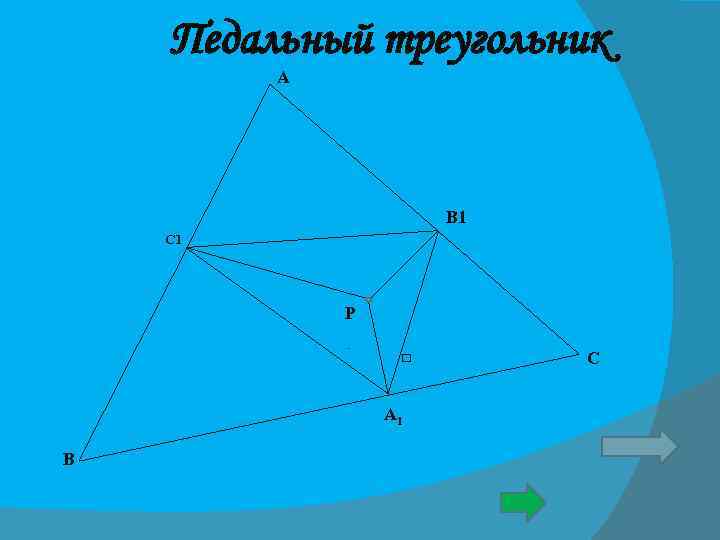Педальный треугольник А В 1 С 1 Р А 1 В С

Эвристическая беседа 1. Рассмотрим произвольный треугольник АВС и углы АС 1 Р и АВ 1 Р. Чему они равняются? 2. На какой отрезок опираются данные углы? 3. Исходя из этого, какую теорему вы вспоминаете? 4. Чем является АР? 5. Можно ли описать около треугольника АВ 1 С 1 окружность? 6. Будут лежать точки Р, В 1, С 1 на этой окружности?

Эвристическая беседа 7. Рассмотрим произвольный треугольник АВ 1 С 1. Какая существует зависимость между углами и сторонами этого треугольника? 8. Как записать данную теорему? 9. Применим данную теорему к треугольнику АВ 1 С 1.

Эвристическая беседа 10. Можно ли записать подобные равенства для треугольников А 1 С 1 В и А 1 В 1 С?

Эвристическая беседа 11. Так как мы незнаем чему равны синусы углов, то выразим их из основной теоремы синусов:

Эвристическая беседа 12. Следовательно получаем:

Эвристическая беседа 13. Если нам даны следующие условия: 1. Дан произвольный треугольник. 2. Расстояние от педальной точки до вершин треугольника равны x, y, z. Теорема: « Если расстояние от педальной точки до вершин треугольника равны x, y, z, то длины сторон педального треугольника равны. »

План. 1. РС 1 В 1 с диаметром АР. 2. В 1 С 1 =АР С 1 А 1 = А 1 В 1 =

Доказательство. Рассмотрим произвольный треугольник АВС треугольник АВ 1 С 1. АС 1 В= АВ 1 Р=90 По теореме об угле опирающемся на диаметр окружности следует, что Р, С 1, В 1 окружности Где -описанная окружность около треугольника АС 1 В 1. .

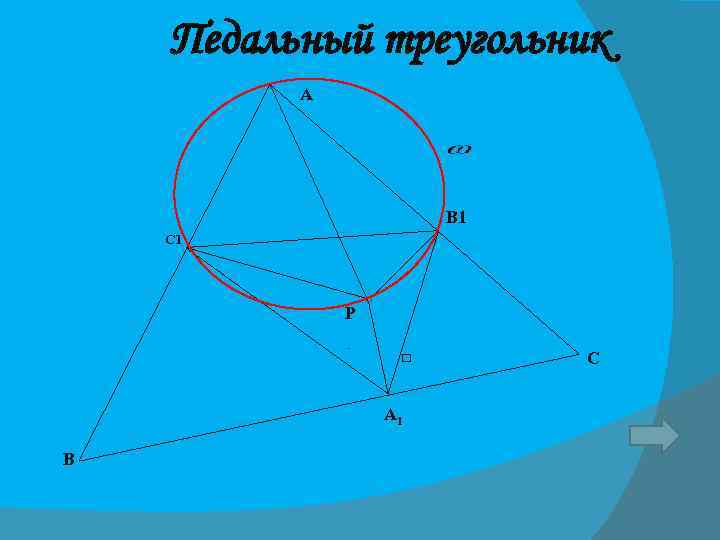Педальный треугольник А В 1 С 1 Р А 1 В С

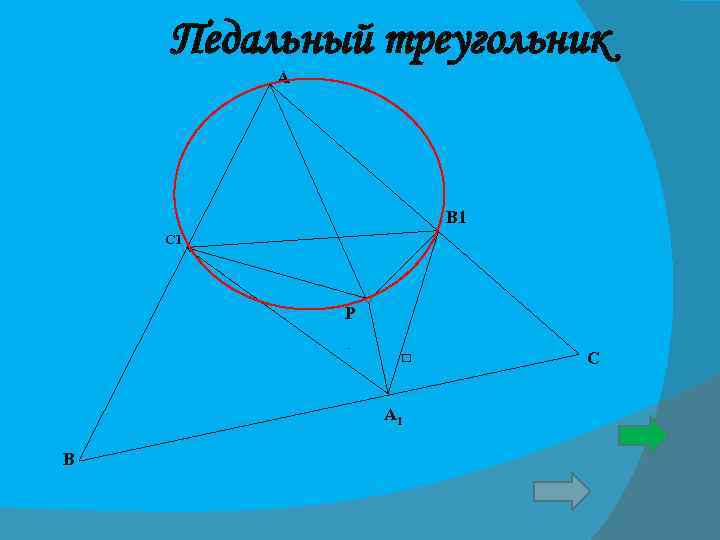Педальный треугольник А В 1 С 1 Р А 1 В С

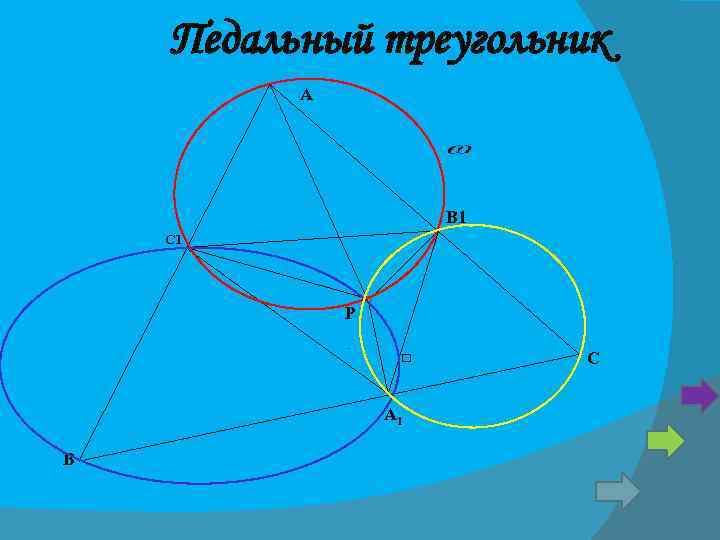Педальный треугольник А В 1 С 1 Р А 1 В С