Опис плоских графічних об єктів за допомогою опорних областей

Опис плоских графічних об’єктів за допомогою опорних областей

Нехай креслення деякого плоского графічного об’єкту (плоскої фігури) являє криву, яку можна описати рівнянням f(x, y)=0 або -f(x, y)=0.

Нехай при підстановці координат х і у будь-якої точки, яка належить у області, що лежить усередині кривої, значення функції буде позитивним, тоді при підстановці координат х і у будь-якої точки, яка лежить поза кривою – негативним. Тоді у другому випадку для усіх точок області, розташованої усередині кривої значення функції буде негативним, а для усіх точок області поза кривою, - позитивними.

Область множини точок, для яких функція приймає ненегативні значення, назвемо опорною областю А функції. Плоский графічний об’єкт, що показаний на рис. , має опорну область А: f(x, y) 0.

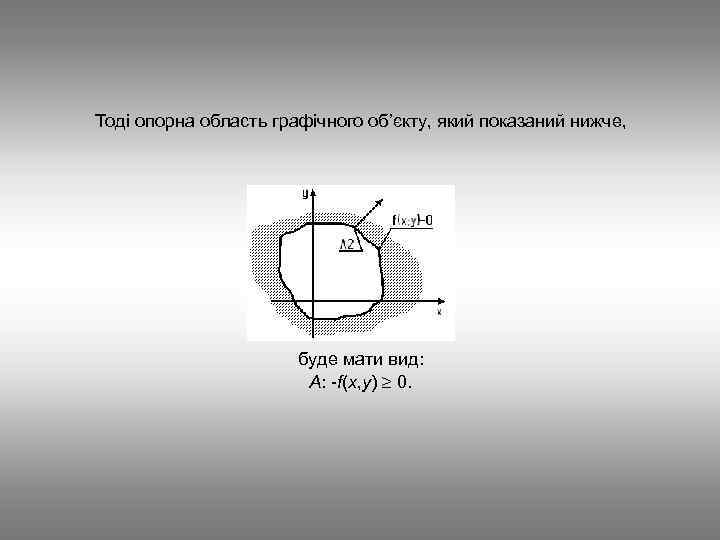
Тоді опорна область графічного об’єкту, який показаний нижче, буде мати вид: А: -f(x, y) 0.

Опорною областю А функції f(x, y) А: f(x, y) 0 називається така область, яка складається з множини точок площини OXY, в яких функція f(x, y) буде приймати ненегативні значення.

Якщо з опорної області А функції f(x, y) виділити область В, де f(x, y)=0, то така область В називається кресленням функції. Креслення функції - це множина точок опорної області, в яких значення функції дорівнює нулю.

Причому креслення функції розбиває площину на дві частини (перша - точки, які знаходяться по одну сторону лінії, яка є кресленням функції і друга - точки, які лежать з іншої сторони). Якщо підставити у функцію координати будь-якої точки з першої частини, то значення функції буде дорівнювати певному числу (яке буде більше або менше нуля). Тобто буде мати місце нерівність змісту f(x, у) 0 або f(x, у) 0. Якщо у функцію підставити координати будь – якої точки з другої частини – нерівність буде мати протилежне значення. Таким чином, креслення функції розділяє площину на дві частини, у яких функція має протилежні по знаку значення.

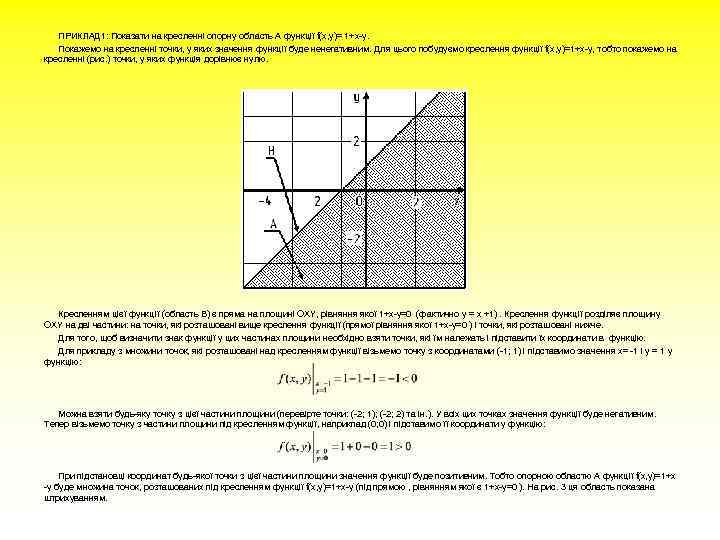
ПРИКЛАД 1: Показати на кресленні опорну область А функції f(x, у)= 1+х-у. Покажемо на кресленні точки, у яких значення функції буде ненегативним. Для цього побудуємо креслення функції f(x, у)=1+х-у, тобто покажемо на кресленні (рис. ) точки, у яких функція дорівнює нулю. Кресленням цієї функції (область В) є пряма на площині OXY, рівняння якої 1+х-у=0 (фактично у = х +1). Креслення функції розділяє площину OXY на дві частини: на точки, які розташовані вище креслення функції (прямої рівняння якої 1+х-у=0 ) і точки, які розташовані нижче. Для того, щоб визначити знак функції у цих частинах площини необхідно взяти точки, які їм належать і підставити їх координати в функцію. Для прикладу з множини точок, які розташовані над кресленням функції візьмемо точку з координатами (-1; 1) і підставимо значення х= -1 і у = 1 у функцію: Можна взяти будь-яку точку з цієї частини площини (перевірте точки: (-2; 1); (-2; 2) та ін. ). У всіх цих точках значення функції буде негативним. Тепер візьмемо точку з частини площини під кресленням функції, наприклад (0; 0) і підставимо її координати у функцію: При підстановці координат будь-якої точки з цієї частини площини значення функції буде позитивним. Тобто опорною областю А функції f(x, у)=1+х -у буде множина точок, розташованих під кресленням функції f(x, у)=1+х-у (під прямою , рівнянням якої є 1+х-у=0 ). На рис. 3 ця область показана штрихуванням.

Для того, щоб побудувати на площині опорну область функції необхідно: 1. побудувати креслення цієї функції, яке розділить площину на дві частини; 2. визначити якій з двох частин площини належать точки, підстановка координат яких у функцію дає її позитивне значення; 3. нанести означення опорної області.

Опорна область означається стрілкою з полицею. Стрілка повинна перетинати перпендикулярно креслення функції и бути направленою всередину опорної області. На полиці наноситься назва опорної області.

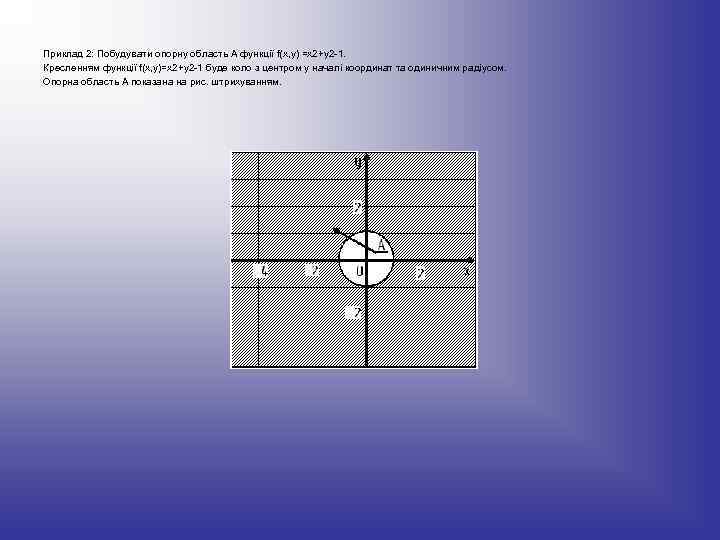
Приклад 2: Побудувати опорну область А функції f(x, у) =х2+y 2 -1. Кресленням функції f(x, у)=х2+y 2 -1 буде коло з центром у началі координат та одиничним радіусом. Опорна область А показана на рис. штрихуванням.

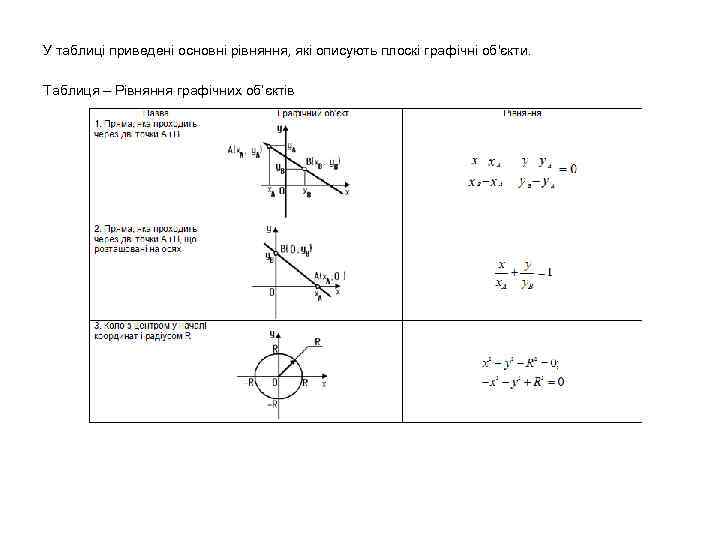
У таблиці приведені основні рівняння, які описують плоскі графічні об'єкти. Таблиця – Рівняння графічних об’єктів

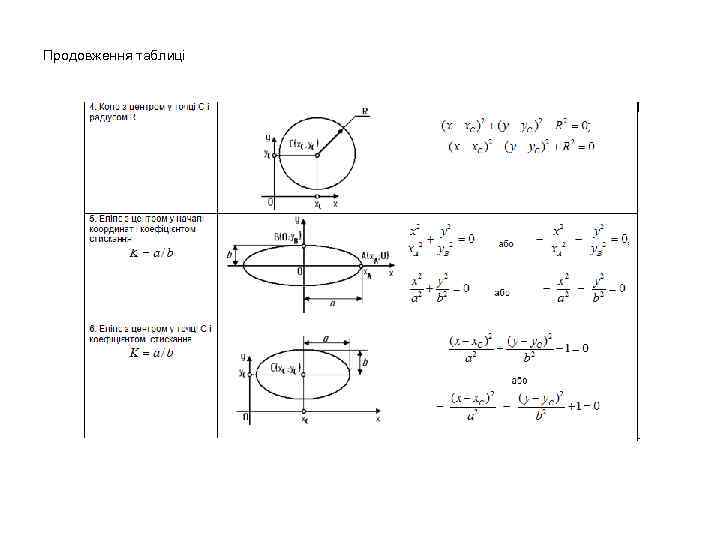
Продовження таблиці

Над множинами точок можна проводити різні логічні операції. Основними з них є такі: • операція об’єднання; • операція перетину; • операція доповнення.

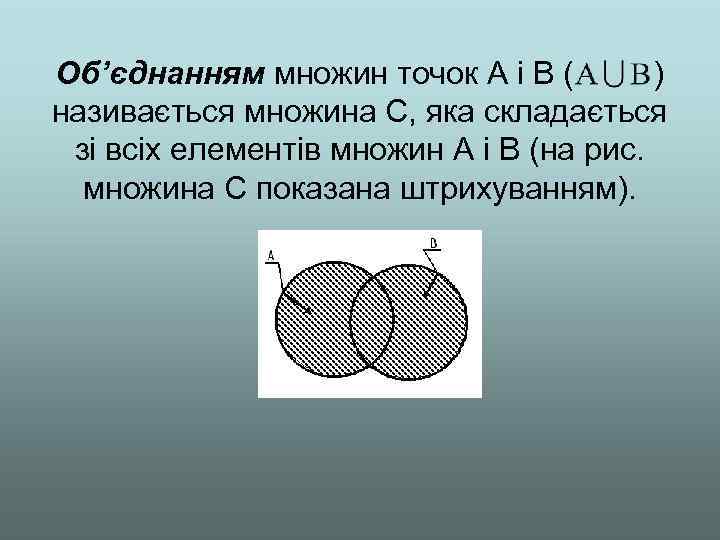
Об’єднанням множин точок A і В ( ) називається множина С, яка складається зі всіх елементів множин А і В (на рис. множина С показана штрихуванням).

Перетином множин точок А і В ( ) називається множину точок D, яка складається з елементів, що належать множинам А і В одночасно (на рис. множина D показана штрихуванням).

Доповненням множини А називається множина , яка складається зі всіх точок, що не належать множині А (на рис. множина показана штрихуванням).

Основні властивості логічних операцій Формальна заміна символу об'єднання на символ перетину, I на 0, і 0 на I не змінює приведених вище рівностей.

Логічною формулою називається символічний запис, що містить позначення декількох множин точок, зв'язаних логічними операціями. Для вказівки черговості виконання логічних операцій допускається використання дужок.

Питання для підготовки до модульного контролю

1. Що називається опорною областю функції? 2. Що називається кресленням функції? 3. Як побудувати креслення функції? 4. Побудувати креслення функції ?

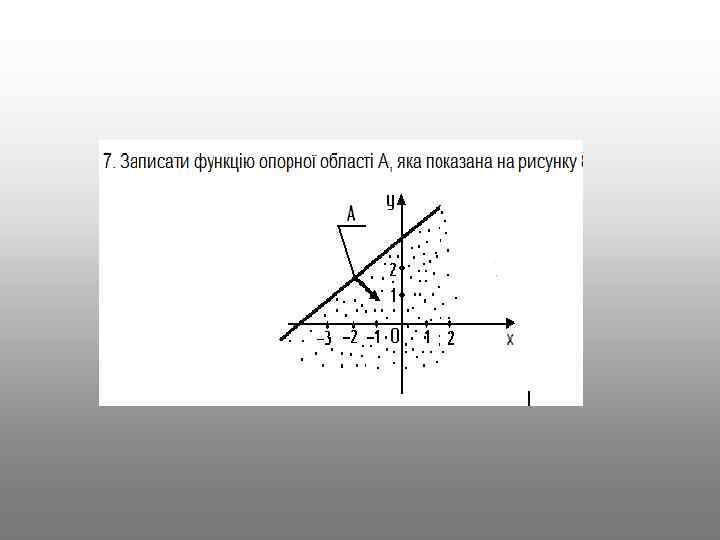
8. Як побудувати на площині опорну область певної функції? 9. Як означається опорна область на кресленні? 10. Запишіть функцію опорної області, яка складається з точок, що лежать усередині кола з центром у точці А(-3; 8) і радіусом 5 одиниць. 11. Які логічні операції можна проводити над множинами точок? Дайте їх визначення.

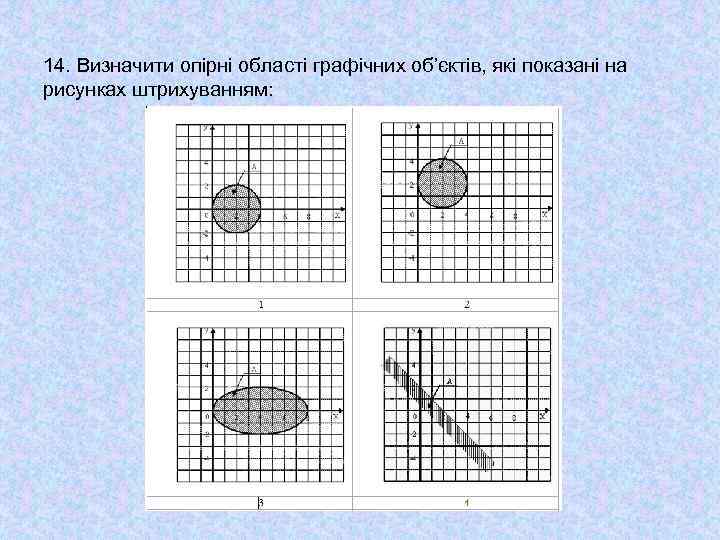
14. Визначити опірні області графічних об’єктів, які показані на рисунках штрихуванням: