ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 7 Стійкість стиснутих стержнів
ЗМІСТ ЛЕКЦІЇ q Ø Ø Розділ 11. Стійкість стиснутих стержнів 11. 1 Поняття про стійкі і нестійкі форми рівноваги 11. 2 Формула Ейлера для визначення критичної сили 11. 3 Вплив умов закріплення стержня на величину критичної сили 11. 4 Межі застосування формули Ейлера. Повний графік критичних напружень. проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 2
11. 1 Поняття про стійкі і нестійкі форми рівноваги Рівновага твердого тіла буває стійкою, нестійкою і байдужою. Приклади з теоретичної механіки (див рис. ): 1. Стержень або кулька, виведені боковою силою зі стану рівноваги, повертаються у початкове положення – стійка рівновага. 2. Стержень і кулька продовжують відхилятися від початкового положення – нестійка рівновага. 3. Стержень або кулька можуть займати довільне положення рівноваги – байдужа рівновага. проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 3
11. 1 Поняття про стійкі і нестійкі форми рівноваги З аналогічними випадками рівноваги зустрічаються при дії стискувальних сил на тверді тіла, що здатні деформуватися. Пружна рівновага деформованого тіла є стійкою, коли після довільно малого відхилення від стану рівноваги тіло намагається повернутися у початковий стан. Пружна рівновага є нестійкою, коли тіло продовжує деформуватися у напрямку наданого йому відхилення. Між стійким і нестійким станом рівноваги існує перехідний, так званий критичний стан, у якому тіло може зберігати і початкову форму рівноваги і відхилятися від неї. проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 4
11. 1 Поняття про стійкі і нестійкі форми рівноваги Критичному стану відповідає значення сили Ркр. При P
11. 1 Поняття про стійкі і нестійкі форми рівноваги При P>Pкр – прямолінійна форма рівноваги не зберігається, стержень набуває нової криволінійної форми рівноваги або руйнується. Найменша стискувальна сила, при якій прямолінійна форма рівноваги стає нестійкою, називається критичною. При P=Pкр напруження в стержні менші границі текучості і тим більше границі міцності, але досягання P=Pкр рівносильне руйнуванню конструкції, яке відбувається раптово без попередніх ознак і тому є небезпечним, оскільки немає можливостей прийняти запобіжні заходи. Згин стержня, що відбувається після втрати стійкості його прямолінійної форми під дією осьових стискувальних сил, називається поздовжнім згином. проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 6
11. 2 Формула Ейлера для визначення критичної сили Нехай під дією сили P>Pкр стержень зігнувся, причому відхилення від прямолінійної форми малі. Запишемо диференціальне рівняння пружної лінії стержня – найменший момент інерції поперечного перерізу стержня; згинальний момент проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 7
11. 2 Формула Ейлера для визначення критичної сили Оскільки знак прогину w, а значить і M(x), і другої похідної протилежні (при даній орієнтації осей координат w>0, а в формулі залишимо мінус: Позначимо Одержимо Загальний розв’язок рівняння проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 8
11. 2 Формула Ейлера для визначення критичної сили Для визначення сталих інтегрування А і В використаємо граничні умови. При Стала А 0, тому що в протилежному разі згину не було б. Значить Звідси Одержимо проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 9
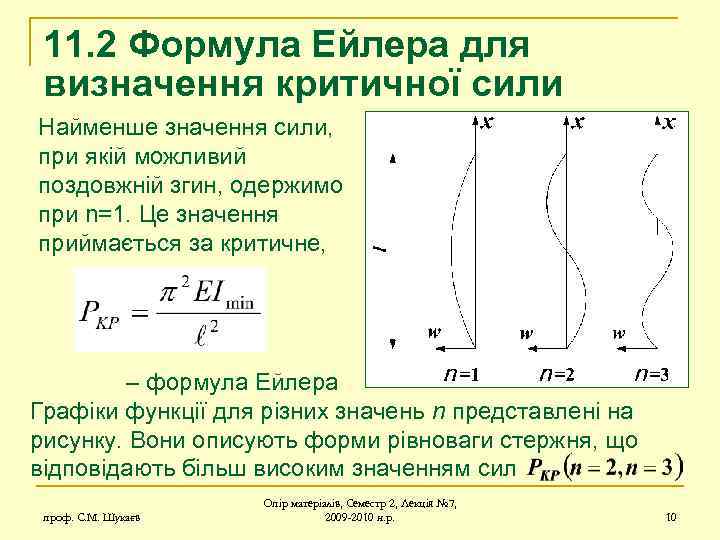11. 2 Формула Ейлера для визначення критичної сили Найменше значення сили, при якій можливий поздовжній згин, одержимо при n=1. Це значення приймається за критичне, – формула Ейлера Графіки функції для різних значень n представлені на рисунку. Вони описують форми рівноваги стержня, що відповідають більш високим значенням сил проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 10
11. 3 Вплив умов закріплення стержня на величину критичної сили проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 11
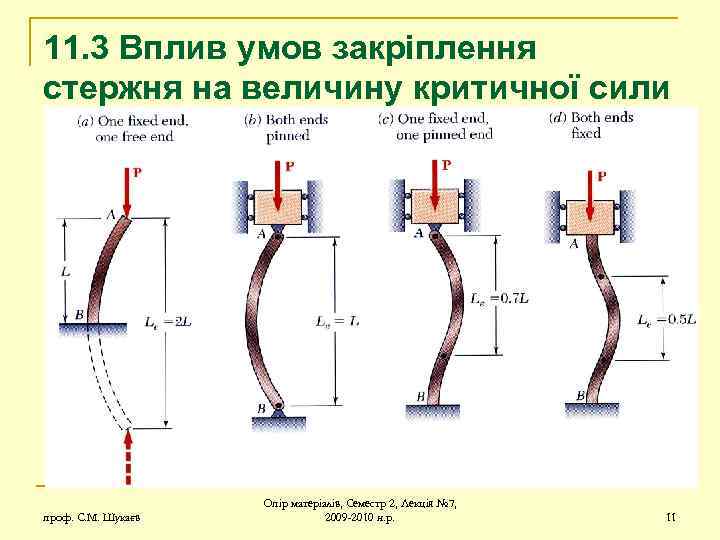
11. 3 Вплив умов закріплення стержня на величину критичної сили На рисунку вказані схеми з різними умовами закріплення, до яких також можна застосовувати формулу Ейлера. Розглянемо вигнуту вісь в кожному випадку як половину синусоїди на частині довжини стержня. Для схеми а) формулу Ейлера можна застосувати, якщо розглянути стержень довжиною 2 l. Для схеми d) – 0, 5 l; Для схеми c) – 0, 7 l. Таким чином, перелічені схеми закріплення стержня можна звести до формули Ейлера, якщо ввести коефіцієнт зведення довжини. Коефіцієнт зведення довжини проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 12
11. 4 Межі застосування формули Ейлера. Повний графік критичних напружень. Критичні напруження в стиснутому стержні де А –площа поперечного перерізу стержня. Враховуючи що , де – мінімальний радіус інерції перерізу стержня, одержимо 13
11. 4 Межі застосування формули Ейлера. Повний графік критичних напружень Введемо поняття гнучкості стержня яка дорівнює відношенню зведеної довжини стержня до радіуса інерції перерізу. Остаточно отримаємо Щоб забезпечити високу стійкість заданого стержня, його поперечний переріз необхідно розташовувати відносно осей y, z так, щоб різниця між гнучкостями в обох площинах була найменша. проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 14
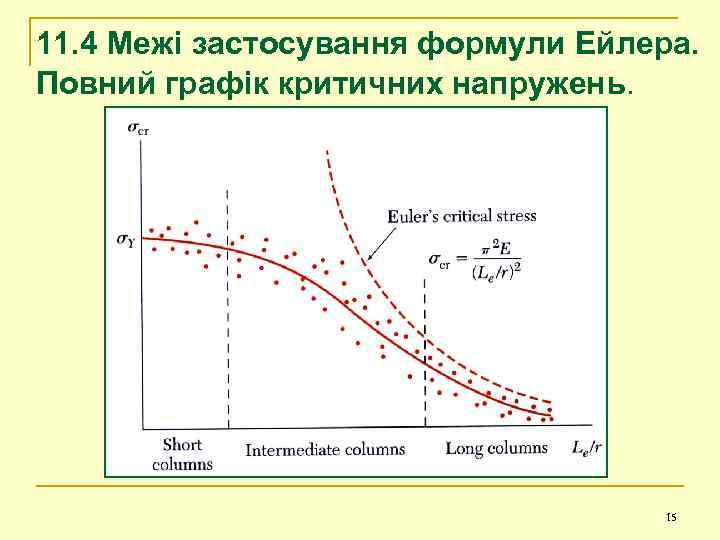11. 4 Межі застосування формули Ейлера. Повний графік критичних напружень. 15
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Семестр 2, Лекція № 7, 2009 -2010 н. р. 16