 ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 4 Енергетичні методи визначення переміщень проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р.
ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 4 Енергетичні методи визначення переміщень проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р.
 ЗМІСТ ЛЕКЦІЇ q Розділ 9. Енергетичні методи визначення переміщень 9. 3 Метод Максвелла – Мора 9. 4 Обчислення інтеграла Мора способом Верещагіна 9. 5 Теореми про взаємність робіт і переміщень проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 2
ЗМІСТ ЛЕКЦІЇ q Розділ 9. Енергетичні методи визначення переміщень 9. 3 Метод Максвелла – Мора 9. 4 Обчислення інтеграла Мора способом Верещагіна 9. 5 Теореми про взаємність робіт і переміщень проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 2
 9. 3 Метод Максвелла – Мора У загальному випадку аналітичні вирази можуть бути різними на різних ділянках, тому замість попередньої формули Мора записуємо так: де n – число ділянок; і – номер довільної ділянки. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 3
9. 3 Метод Максвелла – Мора У загальному випадку аналітичні вирази можуть бути різними на різних ділянках, тому замість попередньої формули Мора записуємо так: де n – число ділянок; і – номер довільної ділянки. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 3
 8. 3 Метод Максвелла – Мора У більшості випадків при визначенні переміщень у балках та рамах можна знехтувати впливом повздовжніх деформацій і деформацій зсуву. Тоді формула Мора приймає вигляд: Помилка! Для плоскої системи сил: Формула Максвелла Якщо розраховуються шарнірні ферми, які утворені прямими стержнями, то у формулі Мора зберігається тільки складова, яка містить повздовжню силу. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 4
8. 3 Метод Максвелла – Мора У більшості випадків при визначенні переміщень у балках та рамах можна знехтувати впливом повздовжніх деформацій і деформацій зсуву. Тоді формула Мора приймає вигляд: Помилка! Для плоскої системи сил: Формула Максвелла Якщо розраховуються шарнірні ферми, які утворені прямими стержнями, то у формулі Мора зберігається тільки складова, яка містить повздовжню силу. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 4
 8. 3 Метод Максвелла – Мора Можна вказати наступний порядок визначення переміщень за методом Мора: • Будують допоміжну систему, яка навантажується одиничним навантаженням у точці, де треба визначити переміщення. При визначенні лінійних переміщень у заданому напрямку прикладають одиничну силу. При визначенні кута повороту прикладають одиничний момент. • Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої і додаткової систем. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 5
8. 3 Метод Максвелла – Мора Можна вказати наступний порядок визначення переміщень за методом Мора: • Будують допоміжну систему, яка навантажується одиничним навантаженням у точці, де треба визначити переміщення. При визначенні лінійних переміщень у заданому напрямку прикладають одиничну силу. При визначенні кута повороту прикладають одиничний момент. • Для кожної ділянки системи записують вирази силових факторів у довільному перерізі заданої і додаткової систем. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 5
 8. 3 Метод Максвелла – Мора • Обчислюємо інтеграли Мора по ділянкам в межах всієї системи. • Якщо обчислене переміщення має додатній знак, то це означає, що його напрямок збігається з напрямком дії одиничної сили. Від’ємний знак вказує на те, що дійсний напрямок переміщення є протилежним до напрямку одиничної сили. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 6
8. 3 Метод Максвелла – Мора • Обчислюємо інтеграли Мора по ділянкам в межах всієї системи. • Якщо обчислене переміщення має додатній знак, то це означає, що його напрямок збігається з напрямком дії одиничної сили. Від’ємний знак вказує на те, що дійсний напрямок переміщення є протилежним до напрямку одиничної сили. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 6
 8. 4 Обчислення інтеграла Мора способом Верещагіна Головним недоліком визначення переміщень за методом Мора є необхідність складання аналітичних виразів підінтегральних функцій. Це особливо важко зробити при визначенні переміщень в стержневих системах, які мають багато ділянок. Обчислення інтеграла Мора суттєво спрощується, якщо одна з епюр (силова або одинична) є прямою лінією. Така умова завжди виконується для систем, які складаються з прямих стержнів, так як при цьому епюри від одиничного навантаження завжди є прямими лініями. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 7
8. 4 Обчислення інтеграла Мора способом Верещагіна Головним недоліком визначення переміщень за методом Мора є необхідність складання аналітичних виразів підінтегральних функцій. Це особливо важко зробити при визначенні переміщень в стержневих системах, які мають багато ділянок. Обчислення інтеграла Мора суттєво спрощується, якщо одна з епюр (силова або одинична) є прямою лінією. Така умова завжди виконується для систем, які складаються з прямих стержнів, так як при цьому епюри від одиничного навантаження завжди є прямими лініями. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 7
 8. 4 Обчислення інтеграла Мора способом Верещагіна С –– центр ваги силової опори Мр - статичний момент площі відносно осі О-О. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 8
8. 4 Обчислення інтеграла Мора способом Верещагіна С –– центр ваги силової опори Мр - статичний момент площі відносно осі О-О. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 8
 8. 4 Обчислення інтеграла Мора способом Верещагіна Відповідно до графоаналітичного методу Верещагіна інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження на ординату прямолінійної епюри від одиничного навантаження Mci, яка розташована під центром ваги силової епюри. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 9
8. 4 Обчислення інтеграла Мора способом Верещагіна Відповідно до графоаналітичного методу Верещагіна інтеграл Мора дорівнює добутку площі епюри від зовнішнього навантаження на ординату прямолінійної епюри від одиничного навантаження Mci, яка розташована під центром ваги силової епюри. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 9
 8. 4 Обчислення інтеграла Мора способом Верещагіна Поради до застосування способу Верещагіна 1). Важливо, щоб ордината була взята обов’язково з прямолінійної епюри. 2). Якщо обидві епюри є прямолінійними, то ординату можна взяти з будь-якої з них. 3). Якщо силова епюра і одинична епюра є протилежними за знаком, то результат множення епюр має від’ємний знак. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 10
8. 4 Обчислення інтеграла Мора способом Верещагіна Поради до застосування способу Верещагіна 1). Важливо, щоб ордината була взята обов’язково з прямолінійної епюри. 2). Якщо обидві епюри є прямолінійними, то ординату можна взяти з будь-якої з них. 3). Якщо силова епюра і одинична епюра є протилежними за знаком, то результат множення епюр має від’ємний знак. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 10
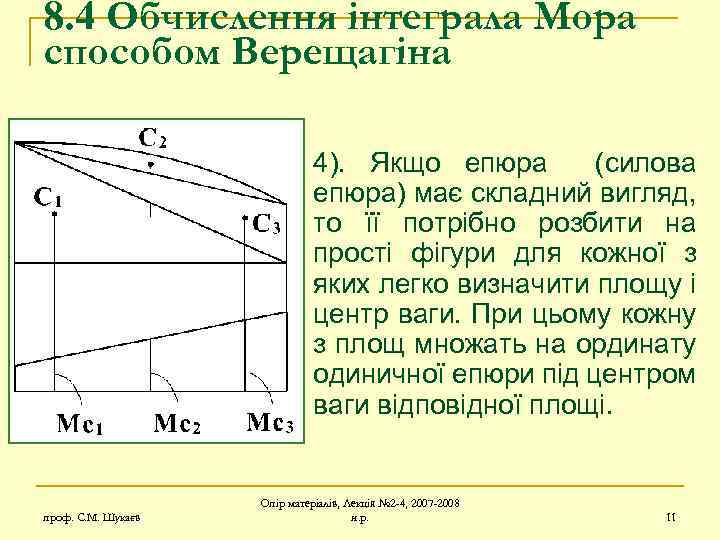 8. 4 Обчислення інтеграла Мора способом Верещагіна 4). Якщо епюра (силова епюра) має складний вигляд, то її потрібно розбити на прості фігури для кожної з яких легко визначити площу і центр ваги. При цьому кожну з площ множать на ординату одиничної епюри під центром ваги відповідної площі. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 11
8. 4 Обчислення інтеграла Мора способом Верещагіна 4). Якщо епюра (силова епюра) має складний вигляд, то її потрібно розбити на прості фігури для кожної з яких легко визначити площу і центр ваги. При цьому кожну з площ множать на ординату одиничної епюри під центром ваги відповідної площі. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 11
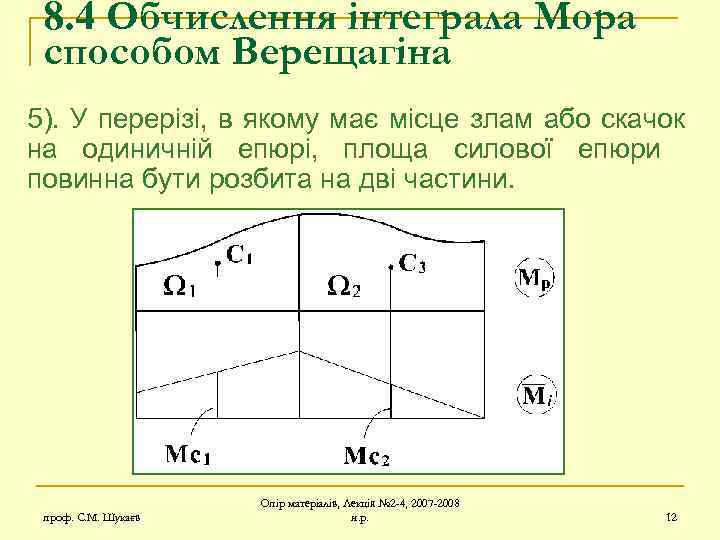 8. 4 Обчислення інтеграла Мора способом Верещагіна 5). У перерізі, в якому має місце злам або скачок на одиничній епюрі, площа силової епюри повинна бути розбита на дві частини. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 12
8. 4 Обчислення інтеграла Мора способом Верещагіна 5). У перерізі, в якому має місце злам або скачок на одиничній епюрі, площа силової епюри повинна бути розбита на дві частини. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 12
 8. 4 Обчислення інтеграла Мора способом Верещагіна Увага! При використанні правила Верещагіна треба пам’ятати про обмеження. Не можна використовувати правило для криволінійних стержнів (обидві епюри є криволінійними) та для стержнів із неперервним змінним перерізом. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 13
8. 4 Обчислення інтеграла Мора способом Верещагіна Увага! При використанні правила Верещагіна треба пам’ятати про обмеження. Не можна використовувати правило для криволінійних стержнів (обидві епюри є криволінійними) та для стержнів із неперервним змінним перерізом. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 13
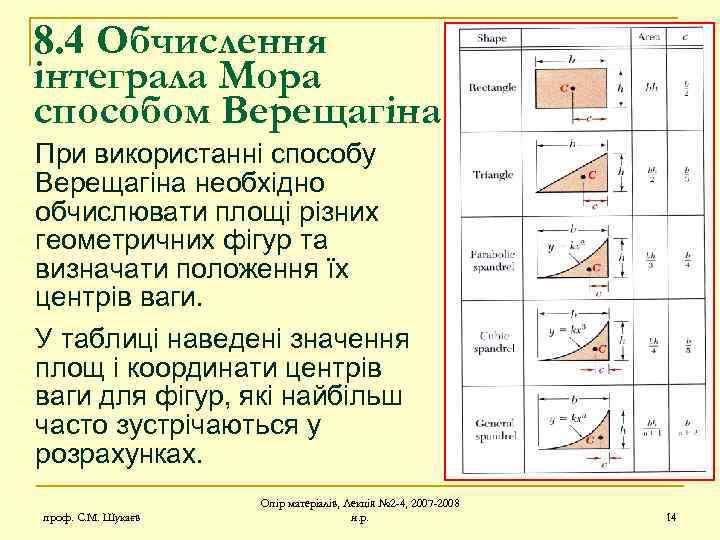 8. 4 Обчислення інтеграла Мора способом Верещагіна При використанні способу Верещагіна необхідно обчислювати площі різних геометричних фігур та визначати положення їх центрів ваги. У таблиці наведені значення площ і координати центрів ваги для фігур, які найбільш часто зустрічаються у розрахунках. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 14
8. 4 Обчислення інтеграла Мора способом Верещагіна При використанні способу Верещагіна необхідно обчислювати площі різних геометричних фігур та визначати положення їх центрів ваги. У таблиці наведені значення площ і координати центрів ваги для фігур, які найбільш часто зустрічаються у розрахунках. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 14
 8. 5 Теореми про взаємність робіт і переміщень Теорема про взаємність робіт, подібно до теореми Кастільяно, відноситься до числа загальних теорем опору матеріалів. Теорема прямо витікає з принципу незалежності дії сил і застосовується до всіх систем, для яких цей принцип є справедливим. У відповідності з цим принципом переміщення та внутрішні сили, які виникають в пружному тілі, вважаються незалежними від послідовності прикладання зовнішніх сил. Якщо до системи прикладається кілька сил, то тоді можна визначити внутрішні сили, напруження, переміщення та деформації від кожної сили окремо. Потім результат дії всіх сил отримують, як суму дії кожної сили. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 15
8. 5 Теореми про взаємність робіт і переміщень Теорема про взаємність робіт, подібно до теореми Кастільяно, відноситься до числа загальних теорем опору матеріалів. Теорема прямо витікає з принципу незалежності дії сил і застосовується до всіх систем, для яких цей принцип є справедливим. У відповідності з цим принципом переміщення та внутрішні сили, які виникають в пружному тілі, вважаються незалежними від послідовності прикладання зовнішніх сил. Якщо до системи прикладається кілька сил, то тоді можна визначити внутрішні сили, напруження, переміщення та деформації від кожної сили окремо. Потім результат дії всіх сил отримують, як суму дії кожної сили. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 15
 8. 5 Теореми про взаємність робіт і переміщень Розглянемо тіло, до якого прикладена сила P 1 в точці 1 та сила P 2 в точці 2. Припускаючи, що до системи може бути застосований принцип незалежності дії сил, визначимо роботу, яку виконують сили P 1 і P 2 при прямій та зворотній послідовності прикладання сил. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 16
8. 5 Теореми про взаємність робіт і переміщень Розглянемо тіло, до якого прикладена сила P 1 в точці 1 та сила P 2 в точці 2. Припускаючи, що до системи може бути застосований принцип незалежності дії сил, визначимо роботу, яку виконують сили P 1 і P 2 при прямій та зворотній послідовності прикладання сил. проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 16
 8. 5 Теореми про взаємність робіт і переміщень Прикладаємо спочатку в точці 1 силу P 1. Ця сила виконує роботу де 11 - переміщення точки 1 у напрямку сили P 1, яке викликане силою. Прикладаємо в точці 2 силу , виконує роботу. Одночасно виконані роботи і сили , оскільки прикладанні сили відбудеться і переміщення точки 1. Робота сили - - переміщення точки 1 по напрямку сили під дією сили. Тепер прикладемо силу , а потім силу : - формула теореми взаємності робіт проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 17
8. 5 Теореми про взаємність робіт і переміщень Прикладаємо спочатку в точці 1 силу P 1. Ця сила виконує роботу де 11 - переміщення точки 1 у напрямку сили P 1, яке викликане силою. Прикладаємо в точці 2 силу , виконує роботу. Одночасно виконані роботи і сили , оскільки прикладанні сили відбудеться і переміщення точки 1. Робота сили - - переміщення точки 1 по напрямку сили під дією сили. Тепер прикладемо силу , а потім силу : - формула теореми взаємності робіт проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 17
 ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 18
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 2 -4, 2007 -2008 н. р. 18


