 ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 3 Енергетичні методи визначення переміщень
ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 3 Енергетичні методи визначення переміщень
 ЗМІСТ ЛЕКЦІЇ q n Розділ 9. Енергетичні методи визначення переміщень 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Ø 9. 2 Теореми Кастільяно Ø 9. 3 Метод Максвелла – Мора проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 2
ЗМІСТ ЛЕКЦІЇ q n Розділ 9. Енергетичні методи визначення переміщень 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Ø 9. 2 Теореми Кастільяно Ø 9. 3 Метод Максвелла – Мора проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 2
 9. Енергетичні методи визначення переміщень Однією з головних задач опору матеріалів (ОМ) є оцінка жорсткості конструкції. Для розв'язання цієї задачі треба визначити переміщення. При вивченні окремих видів деформації стержня серед інших питань розглядалися деякі окремі способи визначення переміщень. Були одержані наступні формули: Розтягання - стискання Кручення Згинання проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 3
9. Енергетичні методи визначення переміщень Однією з головних задач опору матеріалів (ОМ) є оцінка жорсткості конструкції. Для розв'язання цієї задачі треба визначити переміщення. При вивченні окремих видів деформації стержня серед інших питань розглядалися деякі окремі способи визначення переміщень. Були одержані наступні формули: Розтягання - стискання Кручення Згинання проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 3
 9. Енергетичні методи визначення переміщень, продовження Ці рівняння дозволяють визначити будь-яке переміщення в пружній деформаційній системі, але застосування наведених формул виправдано лише у випадку окремого стержня. Якщо пружна система складається з кількох стержнів (рама, ферма), то визначення переміщень за наведеними формулами стає надзвичайно важкою задачею. У таких випадках використовують енергетичні методи визначення переміщень, які легко можна застосувати до системи будь-якої складності і при будь-яких зовнішніх навантаженнях. Якщо необхідно визначити прогин або кут повороту окремого перерізу, а не досліджувати деформацію всього стержня, то енергетичні методи мають значні переваги. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 4
9. Енергетичні методи визначення переміщень, продовження Ці рівняння дозволяють визначити будь-яке переміщення в пружній деформаційній системі, але застосування наведених формул виправдано лише у випадку окремого стержня. Якщо пружна система складається з кількох стержнів (рама, ферма), то визначення переміщень за наведеними формулами стає надзвичайно важкою задачею. У таких випадках використовують енергетичні методи визначення переміщень, які легко можна застосувати до системи будь-якої складності і при будь-яких зовнішніх навантаженнях. Якщо необхідно визначити прогин або кут повороту окремого перерізу, а не досліджувати деформацію всього стержня, то енергетичні методи мають значні переваги. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 4
 9. 1 Потенціальна енергія стержня у загальному випадку навантажування При статичному навантажуванні, коли навантаження зростає повільно від нуля до кінцевого значення, вважається, що вся робота зовнішніх сил (Ap) переходить в потенціальну енергію пружної деформації навантаженого тіла (U), тобто Для визначення потенціальної енергії виділимо елементарну ділянку стержня довжиною dx. Розглянемо загальний випадок навантажування, коли у поперечних перерізах стержня можуть виникати осьові і перерізуючи сили, згинальні і крутні моменти одночасно. Відносно до виділеної елементарної ділянки розглянемо силові фактори, як зовнішні і визначимо роботу, яку вони здійснюють при деформуванні елемента. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 5
9. 1 Потенціальна енергія стержня у загальному випадку навантажування При статичному навантажуванні, коли навантаження зростає повільно від нуля до кінцевого значення, вважається, що вся робота зовнішніх сил (Ap) переходить в потенціальну енергію пружної деформації навантаженого тіла (U), тобто Для визначення потенціальної енергії виділимо елементарну ділянку стержня довжиною dx. Розглянемо загальний випадок навантажування, коли у поперечних перерізах стержня можуть виникати осьові і перерізуючи сили, згинальні і крутні моменти одночасно. Відносно до виділеної елементарної ділянки розглянемо силові фактори, як зовнішні і визначимо роботу, яку вони здійснюють при деформуванні елемента. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 5
 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Увага! Важливо відзначити, що кожний фактор викликає такі переміщення, на яких решта не здійснює роботи. Наприклад, під дією моменту кручення виникає кут повороту перерізу відносно осі х. На цьому кутовому переміщенні роботу здійснює тільки момент кручення. Таким чином, потенціальна енергія елемента може розглядатися, як сума незалежних робіт кожного з 6 силових факторів. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 6
9. 1 Потенціальна енергія стержня у загальному випадку навантажування Увага! Важливо відзначити, що кожний фактор викликає такі переміщення, на яких решта не здійснює роботи. Наприклад, під дією моменту кручення виникає кут повороту перерізу відносно осі х. На цьому кутовому переміщенні роботу здійснює тільки момент кручення. Таким чином, потенціальна енергія елемента може розглядатися, як сума незалежних робіт кожного з 6 силових факторів. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 6
 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Раніше були знайдені величини потенціальної енергії для: - розтягання – стискання - кручення Аналогічно можна записати вирази для: - зсуву - згинання проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 7
9. 1 Потенціальна енергія стержня у загальному випадку навантажування Раніше були знайдені величини потенціальної енергії для: - розтягання – стискання - кручення Аналогічно можна записати вирази для: - зсуву - згинання проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 7
 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Використовуючи принцип незалежності дії сил, одержуємо: Для того, щоб визначити потенціальну енергію всього стержня, цей вираз необхідно проінтегрувати по довжині. k. Y, k. Z - коефіцієнти, які залежать від форми поперечного перерізу. Для більшості систем, в яких елементи працюють на згин і кручення, останні три складові значно менші трьох перших. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 8
9. 1 Потенціальна енергія стержня у загальному випадку навантажування Використовуючи принцип незалежності дії сил, одержуємо: Для того, щоб визначити потенціальну енергію всього стержня, цей вираз необхідно проінтегрувати по довжині. k. Y, k. Z - коефіцієнти, які залежать від форми поперечного перерізу. Для більшості систем, в яких елементи працюють на згин і кручення, останні три складові значно менші трьох перших. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 8
 9. 1 Потенціальна енергія стержня у загальному випадку навантажування Із наведених формул для визначення потенціальної енергії деформації при розтяганні-стисканні, крученні, згинанні та зсуві можна зробити висновки про те, що потенціальна енергія знаходиться, як половина добутку зовнішнього силового фактора на відповідне переміщення. Якщо замінити зовнішні силові фактори якою-небудь узагальненою величиною, наприклад, узагальненою силою (P), а переміщення при будь-якій деформації узагальненим переміщенням (Δ), то потенціальну енергію можна розрахувати так У загальному випадку формула має такий вигляд: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. Математичний запис теореми Клапейрона 9
9. 1 Потенціальна енергія стержня у загальному випадку навантажування Із наведених формул для визначення потенціальної енергії деформації при розтяганні-стисканні, крученні, згинанні та зсуві можна зробити висновки про те, що потенціальна енергія знаходиться, як половина добутку зовнішнього силового фактора на відповідне переміщення. Якщо замінити зовнішні силові фактори якою-небудь узагальненою величиною, наприклад, узагальненою силою (P), а переміщення при будь-якій деформації узагальненим переміщенням (Δ), то потенціальну енергію можна розрахувати так У загальному випадку формула має такий вигляд: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. Математичний запис теореми Клапейрона 9
 9. 2 Теореми Кастільяно Перша теорема Кастільяно Carlo Alberto Castigliano Якщо виразити потенціальну енергію деформації як функцію незалежних узагальнених переміщень, то можна довести, що частинна похідна від потенціальної енергії пружної деформації системи по узагальненому переміщенню дорівнює відповідній узагальненій силі: (1847 - 1884) Ця теорема відома у вітчизняній літературі як теорема Лагранжа. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 10
9. 2 Теореми Кастільяно Перша теорема Кастільяно Carlo Alberto Castigliano Якщо виразити потенціальну енергію деформації як функцію незалежних узагальнених переміщень, то можна довести, що частинна похідна від потенціальної енергії пружної деформації системи по узагальненому переміщенню дорівнює відповідній узагальненій силі: (1847 - 1884) Ця теорема відома у вітчизняній літературі як теорема Лагранжа. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 10
 9. 2 Теореми Кастільяно Друга теорема Кастільяно Якщо виразити потенціальну енергію деформації як функцію незалежних зовнішніх сил, то можна довести, що частинна похідна від потенціальної енергії пружної деформації по узагальненій силі дорівнює відповідному узагальненому переміщенню: Увага! Слід відзначити, що знайдене за цією формулою узагальнене переміщення має знак плюс, якщо воно співпадає за напрямом із узагальненою силою. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 11
9. 2 Теореми Кастільяно Друга теорема Кастільяно Якщо виразити потенціальну енергію деформації як функцію незалежних зовнішніх сил, то можна довести, що частинна похідна від потенціальної енергії пружної деформації по узагальненій силі дорівнює відповідному узагальненому переміщенню: Увага! Слід відзначити, що знайдене за цією формулою узагальнене переміщення має знак плюс, якщо воно співпадає за напрямом із узагальненою силою. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 11
 9. 2 Теореми Кастільяно Приклади застосування теореми Кастільяно. Визначимо способом Кастільяно вертикальний прогин кінця В консольної балки. Врахуємо, що Підставивши це значення у формулу для визначення потенціальної енергії, одержимо: тоді проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 12
9. 2 Теореми Кастільяно Приклади застосування теореми Кастільяно. Визначимо способом Кастільяно вертикальний прогин кінця В консольної балки. Врахуємо, що Підставивши це значення у формулу для визначення потенціальної енергії, одержимо: тоді проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 12
 9. 3 Метод Максвелла – Мора James Clerk Maxwell (1831 - 1879) Визначення переміщень за допомогою теореми Кастільяно має той недолік, що дозволяє визначити переміщення тільки в точці прикладання зовнішніх сил і тільки у напрямку дії цих сил. На практиці виникає необхідність визначати переміщення довільних точок тіла у будь-яких напрямках. Christian Otto Mohr (1835 -1918) У 1874 р. Мор узагальнив спосіб розрахунку переміщень, який було запропоновано Максвеллом у 1864 р. для ферм. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 13
9. 3 Метод Максвелла – Мора James Clerk Maxwell (1831 - 1879) Визначення переміщень за допомогою теореми Кастільяно має той недолік, що дозволяє визначити переміщення тільки в точці прикладання зовнішніх сил і тільки у напрямку дії цих сил. На практиці виникає необхідність визначати переміщення довільних точок тіла у будь-яких напрямках. Christian Otto Mohr (1835 -1918) У 1874 р. Мор узагальнив спосіб розрахунку переміщень, який було запропоновано Максвеллом у 1864 р. для ферм. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 13
 9. 3 Метод Максвелла – Мора Визначимо переміщення в точці А у напрямку осі Y. Для цього прикладаємо в точку А у напрямку осі Y фіктивну силу Ф. Внутрішні силові фактори у кожному поперечному перерізі при цьому змінюються на величини, які залежать від сили Ф. Наприклад, момент кручення у довільному перерізі буде мати вигляд: Аналогічно можна записати інші силові фактори: і т. ін. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 14
9. 3 Метод Максвелла – Мора Визначимо переміщення в точці А у напрямку осі Y. Для цього прикладаємо в точку А у напрямку осі Y фіктивну силу Ф. Внутрішні силові фактори у кожному поперечному перерізі при цьому змінюються на величини, які залежать від сили Ф. Наприклад, момент кручення у довільному перерізі буде мати вигляд: Аналогічно можна записати інші силові фактори: і т. ін. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 14
 9. 3 Метод Максвелла – Мора Очевидно, що додаткові силові фактори Mk. Ф, MZФ, … пропорційні фіктивній силі Ф, тому силові фактори можна представити: де - коефіцієнт пропорційності. Якщо розвантажити систему від зовнішнього навантаження і замінити силу Ф одиничною силою, то проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 15
9. 3 Метод Максвелла – Мора Очевидно, що додаткові силові фактори Mk. Ф, MZФ, … пропорційні фіктивній силі Ф, тому силові фактори можна представити: де - коефіцієнт пропорційності. Якщо розвантажити систему від зовнішнього навантаження і замінити силу Ф одиничною силою, то проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 15
 9. 3 Метод Максвелла – Мора Таким чином внутрішні силові фактори, які виникають у поперечному перерізі під дією одиничної сили, яка прикладається у заданій точці і в заданому напрямку. Застосуємо теорему Кастільяно для визначення переміщення в точці А. Для цього запишемо вираз потенціальної енергії пружної деформації в системі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 16
9. 3 Метод Максвелла – Мора Таким чином внутрішні силові фактори, які виникають у поперечному перерізі під дією одиничної сили, яка прикладається у заданій точці і в заданому напрямку. Застосуємо теорему Кастільяно для визначення переміщення в точці А. Для цього запишемо вираз потенціальної енергії пружної деформації в системі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 16
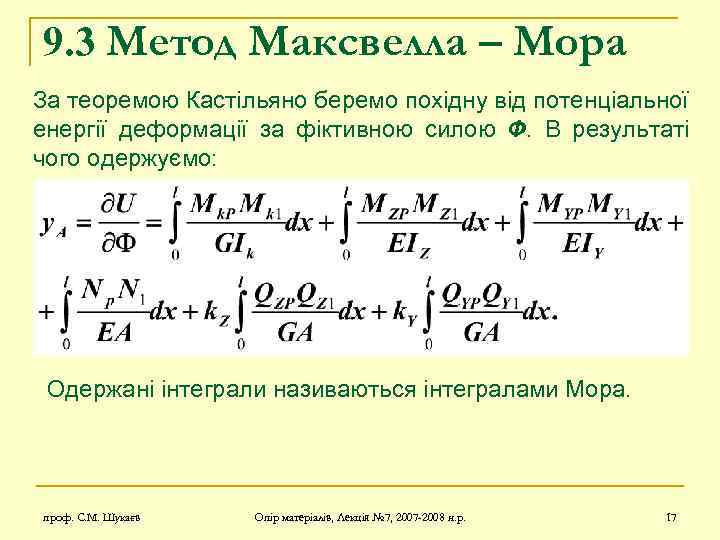 9. 3 Метод Максвелла – Мора За теоремою Кастільяно беремо похідну від потенціальної енергії деформації за фіктивною силою Ф. В результаті чого одержуємо: Одержані інтеграли називаються інтегралами Мора. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 17
9. 3 Метод Максвелла – Мора За теоремою Кастільяно беремо похідну від потенціальної енергії деформації за фіктивною силою Ф. В результаті чого одержуємо: Одержані інтеграли називаються інтегралами Мора. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 17
 ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. Опір матеріалів, Лекція № 12, 2008 р. 18
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. Опір матеріалів, Лекція № 12, 2008 р. 18


