ОПІР МАТЕРІАЛІВ Семестр — 2 Лекція — 11

ОПІР МАТЕРІАЛІВ Семестр - 2 Лекція - 11 Пружні коливання

ЗМІСТ ЛЕКЦІЇ q Ø – – – Розділ 10. Динамічне навантажування 10. 4 Пружні коливання 10. 4. 1 Класифікація механічних коливань 10. 4. 2 Власні гармонічні коливання пружної системи з одним ступенем вільності 10. 4. 3 Вимушені коливання пружної системи з одним ступенем вільності проф. С. М. Шукаєв Опір матеріалів, Лекція № 12, 2008 р. 2

12. 4 Пружні коливання Для того щоб те чи інше тіло було здатне здійснити коливання, воно повинно мати масу та пружність. 12. 4. 1 Класифікація механічних коливань Розрізняють періодичні, майже періодичні та неперіодичні коливання. Періодичним називається такий процес, при якому коливна величина, взята в будь-який момент часу, через певний відрізок часу T (період) має таке саме значення. Математичний вираз періодичної функції: Неперіодичними функціями називаються функції, які не задовільняють зазначеній умові. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 3

12. 4 Пружні коливання Майже періодична функція визначається умовою при будь-якому t, де та - певні сталі величини. Величина , що є функцією , називається майже періодом. Очевидно, якщо - дуже мала величина, порівняно із середнім модулем функції f 1(t) за час t , то майже періодична функція буде близькою до періодичної. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 4

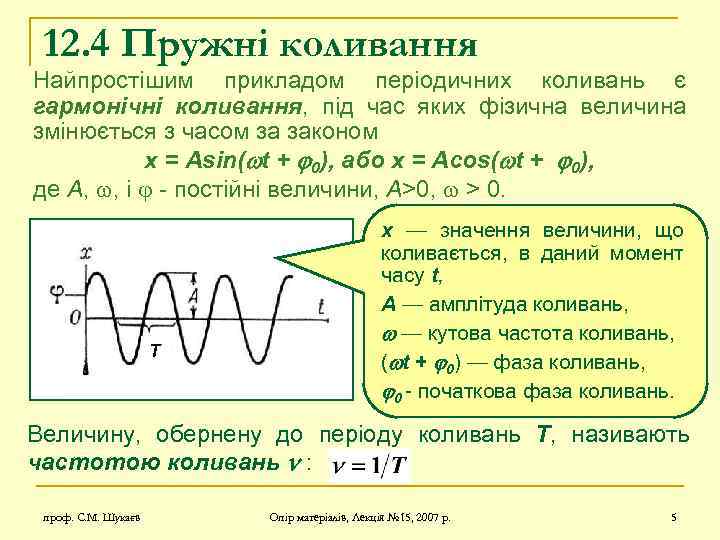12. 4 Пружні коливання Найпростішим прикладом періодичних коливань є гармонічні коливання, під час яких фізична величина змінюється з часом за законом x = Asin( t + 0), або x = Acos( t + 0), де А, , і - постійні величини, А>0, > 0. T х — значення величини, що коливається, в даний момент часу t, А — амплітуда коливань, — кутова частота коливань, ( t + 0) — фаза коливань, 0 - початкова фаза коливань. Величину, обернену до періоду коливань Т, називають частотою коливань : проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 5

12. 4 Пружні коливання Досліджуючи коливальні рухи пружних систем, важливо знати, яка кількість незалежних параметрів визначає положення системи в кожний момент часу. Кількість таких параметрів називають числом ступенів вільності. У найпростіших випадках положення системи може визначатися тільки однією величиною. Такі системи називають системами з одним ступенем вільності. Прикладом коливальної системи з одним ступенем вільності є вантаж, який закріплено на пружині. Якщо механічна система така, що можливі тільки вертикальні переміщення вантажу, і якщо маса пружини мала порівняно з масою вантажу, то положення такої коливальної системи визначається одним параметром – вертикальним переміщенням вантажу. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 6

12. 4 Пружні коливання Класифікуючи механічні коливання за іншими ознаками, розрізняють наступні типи коливань. Власними (вільними) називаються коливання, які виникають в ізольованій системі внаслідок зовнішнього збудження, що спричинює початкові відхилення точок системи від положення рівноваги або початкові швидкості, і тривають потім завдяки внутрішнім пружним силам, які відновлюють рівновагу. Власні коливання є згасаючими. Вимушеними називають коливання пружної системи, які відбуваються при дії на систему (протягом усього періоду коливань) заданих зовнішніх сил, що періодично змінюються і діють неперервно незалежно від коливань у системі. Вимушені коливання є незгасаючими. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 7

12. 4 Пружні коливання Автоколиваннями, або самоколиваннями, пружної системи називають незгасаючі коливання, що підтримуються такими зовнішніми силами, характер дій яких визначається самими коливальними процесами механічної системи. Автоколивання виникають у системі без зовнішньої періодичної дії. Це коливання, які підтримуються внутрішніми джерелами енергії системи. Наприклад, настінний годинник з маятником або наручний механічний годинник - це механічні автоколивальні системи. У годинниках потенціальна енергія тягарця (або стиснутої пружини) поступово, окремими порціями передається маятнику і компенсує втрати на тертя. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 8

12. 4 Пружні коливання На початку 30 -х років минулого сторіччя весь авіаційний світ був шокований рядом авіакатастроф, які відбулися на швидкостях, що для того часу раніше були недосяжними. Досить швидко з'ясувалося, що руйнування відбуваються через вібрацію, яка виникає від дії повітряного потоку. Цей особливий вид автоколивань було названо флатером (англ. flutter = вібрація). Явище флатера пов'язано із взаємним розташуванням центру ваги і центру жорсткості крила та іншими характеристиками літака. Саме флатер довгий час перешкоджав подоланню надзвукового бар'єру — сильна вібрація, перевантаження і страх змушували льотчиків-дослідників відступати. Значний вклад в розв'язання задачі автоколивань авіаційних конструкцій вніс радянський вчений Мстислав Всеволодович Келдиш (академік АН СРСР). проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 9

12. 4 Пружні коливання У наш час флатер в значній мірі досліджено і відомо, як його уникнути. Але раніше він був причиною багатьох аварій літаків, руйнування підвісних мостів і таке ін. 7 листопада 1940 року відбулася грандіозна катастрофа підвісного моста через пролив Такома (США). Загальна довжина моста складала 1662 м, ширина - 12 м. В день катастрофи вітер дув із швидкістю 18 м/сек; частота коливань моста досягала 36 кол/хв, потім частота коливань раптово зменшилася до 14 кол/хв, розпочалися крутильні коливання. У результаті цих складних коливань відбулося руйнування моста. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 10

12. 4 Пружні коливання 12. 4. 2 Власні гармонічні коливання пружної системи з одним ступенем вільності Розглянемо пружну систему, яка представлена на рисунку. Тертям нехтуємо. Використаємо принцип Д’Аламбера для запису диференціального рівняння коливань вантажу. Звідси або Отримане рівняння зветься рівнянням власних коливань, а - колова частота власних коливань. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 11

10. 4 Пружні коливання Рівняння власних коливань має такий загальний розв’язок: де A – амплітуда коливань, 0 - початкова фаза коливань. A і 0 – сталі, що залежать від початкових умов. За початок відліку переміщень обирається положення вантажу, яке відповідає стану рівноваги. Значення найбільших і найменших відхилень xmax та xmin визначають з умов Увага! Фізичні властивості коливальної системи визначають тільки власну частоту коливань ω. Такі параметри як A і 0 залежать від способу виведення системи з рівноваги. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 12

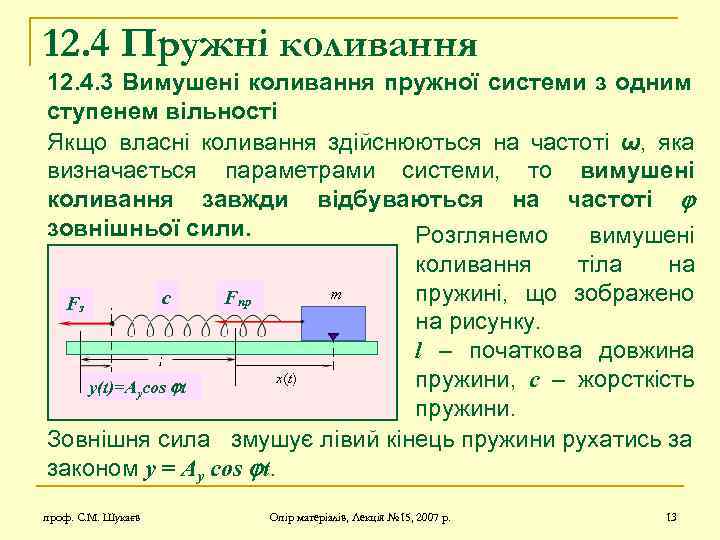12. 4 Пружні коливання 12. 4. 3 Вимушені коливання пружної системи з одним ступенем вільності Якщо власні коливання здійснюються на частоті ω, яка визначається параметрами системи, то вимушені коливання завжди відбуваються на частоті зовнішньої сили. Розглянемо вимушені коливання тіла на пружині, що зображено с Fпр Fз на рисунку. l – початкова довжина пружини, с – жорсткість y(t)=Aycos t пружини. Зовнішня сила змушує лівий кінець пружини рухатись за законом y = Ay cos t. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 13

12. 4 Пружні коливання Якщо лівий кінець пружини зміщено на відстань y, а правий – на відстань x від їх початкового (недеформованого) положення, то видовження пружини Δl дорівнює: Другий закон Ньютона для тіла масою m: У цьому рівнянні сила, що діє на тіло, представлена двома складовими. Перша складова у правій частині – це сила пружності, яка намагається повернути тіло у положення рівноваги (x = 0). Друга складова – зовнішня періодична сила, що діє на тіло. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 14

12. 4 Пружні коливання Рівнянню, що виражає другий закон Ньютона для тіла на пружині при наявності зовнішнього періодичного збурення, можна надати строгу математичну форму, якщо врахувати зв'язок між прискоренням тіла та його координатою: Тоді рівняння вимушених коливань запишеться у вигляді Дане рівняння не враховує силу тертя. На відміну від рівняння власних коливань воно містить дві частоти – частоту власних коливань ω і частоту зовнішньої сили збурення . Вимушені коливання вантажу на пружині здійснюються з частотою зовнішнього збурення за законом проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 15

12. 4 Пружні коливання Амплітуда вимушених коливань Ax і початкова фаза 0 залежать від співвідношення частот ω і амплітуди Ay зовнішньої сили. На низьких частотах, коли << ω, рух тіла масою m, яке закріплено до правого кінця пружини, повторює рух лівого кінця пружини. При цьому x(t) = y(t), і пружина залишається практично недеформованою. Зовнішня сила, яка прикладена до лівого кінця пружини, роботи не виконує, через те, що модуль цієї сили при << ω прямує до нуля. Якщо частота зовнішньої сили наближається до власної частоти ω, виникає різке зростання амплітуди вимушених коливань. Це явище зветься резонансом. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 16

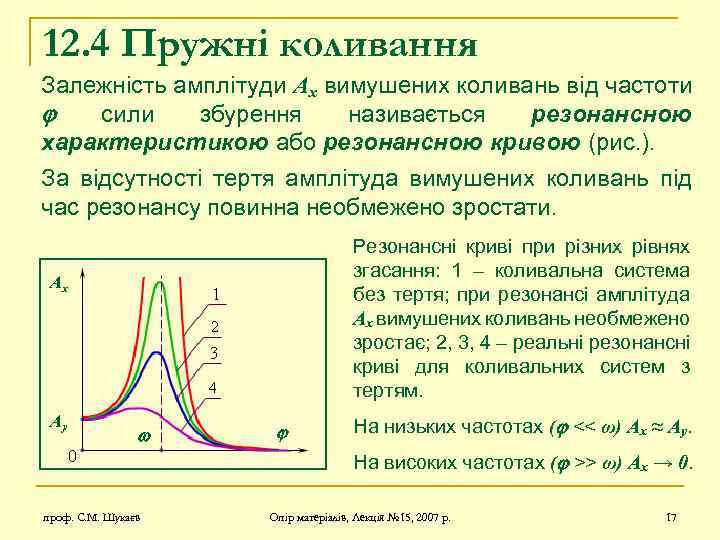12. 4 Пружні коливання Залежність амплітуди Ax вимушених коливань від частоти сили збурення називається резонансною характеристикою або резонансною кривою (рис. ). За відсутності тертя амплітуда вимушених коливань під час резонансу повинна необмежено зростати. Резонансні криві при різних рівнях згасання: 1 – коливальна система без тертя; при резонансі амплітуда Ax вимушених коливань необмежено зростає; 2, 3, 4 – реальні резонансні криві для коливальних систем з тертям. Ax Ay На низьких частотах ( << ω) Ax ≈ Ay. На високих частотах ( >> ω) Ax → 0. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 17

12. 4 Пружні коливання В реальних умовах амплітуда вимушених коливань визначається умовою: робота зовнішньої сили за період коливань повинна дорівнювати втратам механічної енергії за той же час через тертя. Чим менше тертя, тим більша амплітуда вимушених коливань під час резонансу. Явище резонансу може стати причиною руйнування мостів, будівель та інших споруд, якщо власні частоти їх коливань співпадуть з частотою періодично діючої сили, яка виникає, наприклад, через обертання незбалансованого двигуна. Відомий випадок, коли під час резонансу кут закручування валу зріс у шість разів у порівнянні з тим кутом, який був до появи резонансу, — це був випадок руйнування колінчатих валів двигунів «Цеппеліна» під час першого його переліту через Атлантичний океан. проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 18

ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 15, 2007 р. 19