ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція - 8 Основи теорії напруженого і деформованого стану твердого тіла
ЗМІСТ ЛЕКЦІЇ q Ø Ø Ø Розділ 3. Основи теорії напруженого і деформованого стану твердого тіла 3. 7 Пряма і обернена задачі теорії напруженого стану в точці 3. 8 Плоский напружений стан 3. 9 Деформований стан в точці. 3. 10 Залежність між переміщеннями та деформаціями (співвідношення Коші) 3. 11 Рівняння нерозривності деформацій (умова Сен-Венана). проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 2
3. 7 Пряма і обернена задачі теорії напруженого стану в точці В теорії напруженого стану можна виділити дві основні задачі: пряму та обернену. Пряма задача. В точці тіла відомі положення головних площадок і значення головних напружень. Треба знайти нормальні та дотичні напруження, які діють на довільній площадці, положення якої відносно головних площадок відомо. Обернена задача. В деякій точці тіла відомі нормальні та дотичні напруження, які діють на трьох взаємноперпендикулярних площадках, що проходять через дану точку. Треба знайти положення головних площадок та значення головних напружень.
3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання прямої задачі:
3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання оберненої задачі:
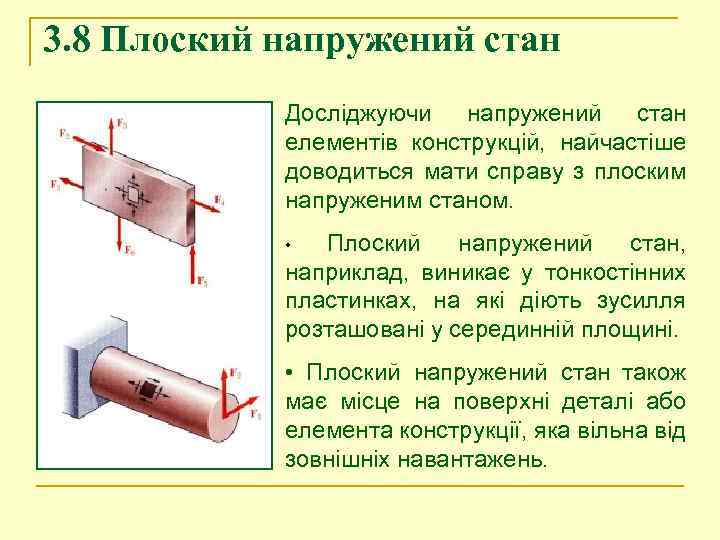3. 8 Плоский напружений стан Досліджуючи напружений стан елементів конструкцій, найчастіше доводиться мати справу з плоским напруженим станом. Плоский напружений стан, наприклад, виникає у тонкостінних пластинках, на які діють зусилля розташовані у серединній площині. • • Плоский напружений стан також має місце на поверхні деталі або елемента конструкції, яка вільна від зовнішніх навантажень.
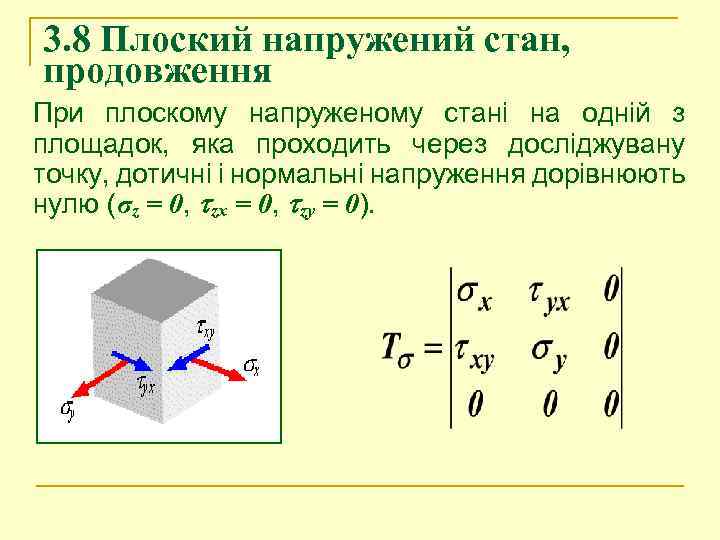3. 8 Плоский напружений стан, продовження При плоскому напруженому стані на одній з площадок, яка проходить через досліджувану точку, дотичні і нормальні напруження дорівнюють нулю (σz = 0, zx = 0, zy = 0).
3. 8 Плоский напружений стан, продовження Головні напруження визначаються з рівняння: В результаті розв’язання даного рівняння отримаємо:
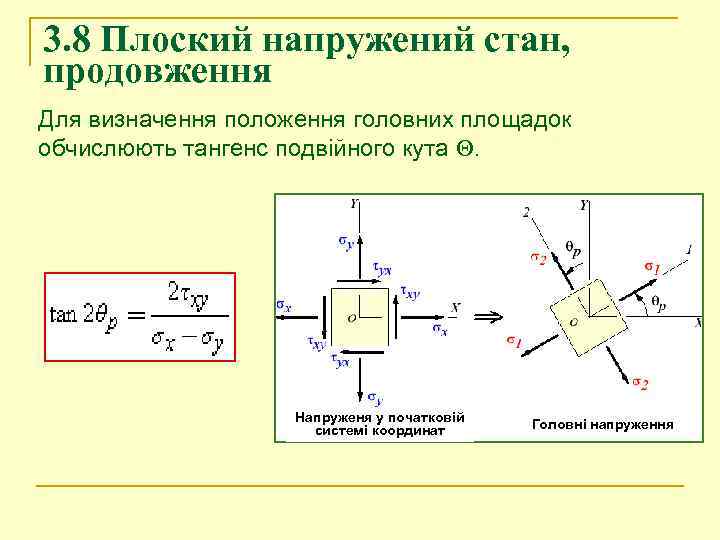3. 8 Плоский напружений стан, продовження Для визначення положення головних площадок обчислюють тангенс подвійного кута . Напруженя у початковій системі координат Головні напруження
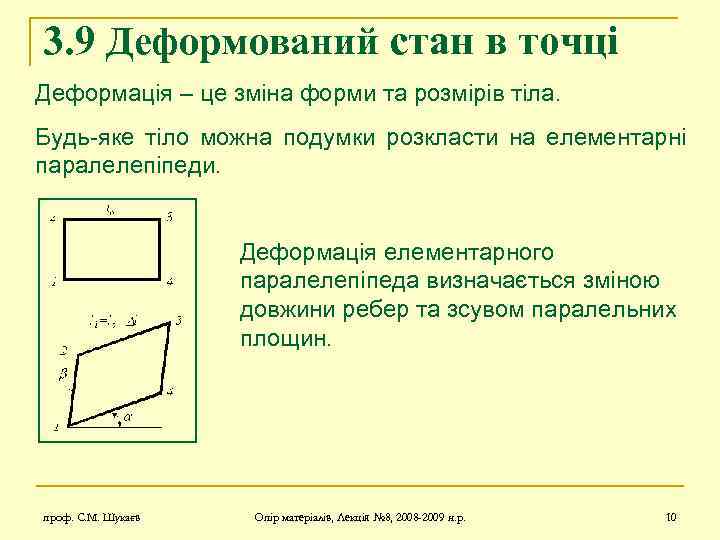3. 9 Деформований стан в точці Деформація – це зміна форми та розмірів тіла. Будь-яке тіло можна подумки розкласти на елементарні паралелепіпеди. Деформація елементарного паралелепіпеда визначається зміною довжини ребер та зсувом паралельних площин. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 10
3. 9 Деформований стан в точці, продовження +y Ðadc = p 2 радіан a +y a Ðadc < p 2 радіан g xy dl y b c c +x Початкова форма b +x dl x + D(dl x ) Здеформована форма Відносні деформації ребер в напрямку осей та відносні зсуви у відповідних площинах визначаються таким чином: проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 11
3. 9 Деформований стан в точці, продовження У загальному випадку маємо: проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 12
3. 9 Деформований стан в точці, продовження Якщо прийняти, що довжини ребер паралелепіпеду наближаються до нуля, то складові деформації будуть визначати повну деформацію навколо досліджуваної точки і утворювати тензор деформації. Можна показати, що для отриманого тензора деформації необхідно брати лише половини кутових деформацій. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 13
3. 9 Деформований стан в точці, продовження Додатнім лінійним деформаціям відповідає видовження уздовж осей координат, від’ємним – укорочення. Додатнім кутовим деформаціям відповідає зменшення кутів між додатнім напруженням осей, а від’ємним збільшення тих самих кутів. Аналіз деформованого стану показує, що він має ті ж властивості, що й напружений стан. Серед множини вісей, які можуть бути проведені через досліджувану точку, існує три взаємно перпендикулярні осі, в системі яких кутові деформації відсутні. Ці осі називаються головними осями деформованого стану, а лінійні деформації в цій системі називаються головними деформаціями. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 14
3. 9 Деформований стан в точці, продовження Визначення головних деформацій виконується приблизно так, як і головних напружень. Розв'язують відповідне кубічне рівняння: Коефіцієнти рівняння є інваріантами тензора деформації при повороті осей координат проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 15
3. 9 Деформований стан в точці, продовження Тензор деформацій через головні деформації записується так: проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 16
3. 9 Деформований стан в точці, продовження Аналогічно теорії напруженого стану, якщо відомі головні деформації в довільній точці, тоді зміна довжини довільного відрізка, який проходить через задану точку і який складає з головними осями кути, косинуси яких l, m, n. При деформації тіла разом з мінімальною кутовою деформацією розглядають також об’ємну деформацію. Зміна об’єму, віднесена до початкового об’єму, називається відносною об’ємною деформацією. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 17
3. 10 Залежність між переміщеннями та деформаціями (співвідношення Коші) Зміна форми тіла пов’язана з переміщенням його точок. Відстань між знаходженням деякої точки А до та після зміни форми тіла називається її повним переміщенням. Переміщення різних точок тіла є різними безперервними функціями координат проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 18
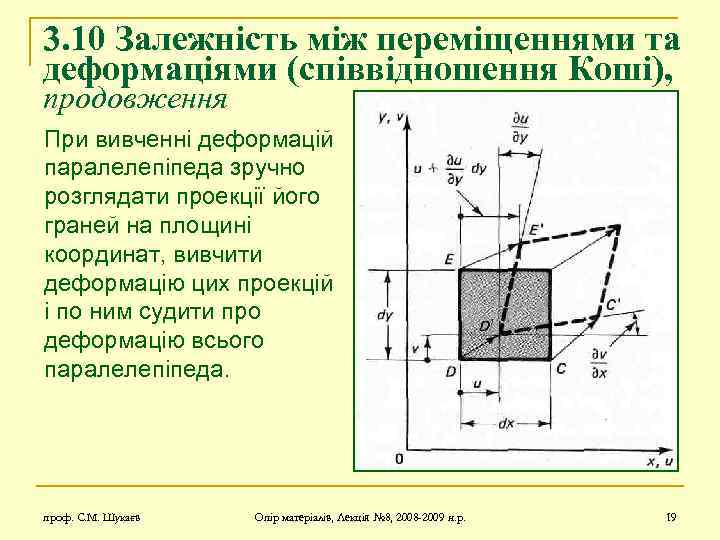3. 10 Залежність між переміщеннями та деформаціями (співвідношення Коші), продовження При вивченні деформацій паралелепіпеда зручно розглядати проекції його граней на площині координат, вивчити деформацію цих проекцій і по ним судити про деформацію всього паралелепіпеда. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 19
3. 10 Залежність між переміщеннями та деформаціями (співвідношення Коші), продовження проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 20
3. 11 Рівняння нерозривності деформацій (умова Сен-Венана) Співвідношення Коші дозволяють простим диференціюванням за відомими переміщеннями u, v, w, як деяких функцій координат точок тіла, визначити компоненти тензора деформацій. Розв’язок оберненої задачі – знаходження переміщень за відомими компонентами деформацій - зводиться до інтегрування системи диференціальних рівнянь Коші. Для існування розв’язків цієї системи необхідна наявність визначених зв’язків між компонентами деформацій, тобто виконання умови інтегрування рівнянь Коші. Ця умова зветься умовою щільності, умовою сумісності або умовою Сен-Венана. проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 21
3. 11 Рівняння нерозривності деформацій (умова Сен-Венана), продовження Ці рівняння отримані французьким вченим Сен-Венаном в 1864 р. У випадку, коли рівняння сумісності задовільні в кожній точці тіла, переміщення u, v, w будуть неперервними функціями координат, що гарантує безперервне перетворення початкової форми тіла (без розривів та пустоти) в кінцеву (деформовану) проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 22
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 8, 2008 -2009 н. р. 23