 ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція - 7 Основи теорії напруженого і деформованого стану твердого тіла проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р.
ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція - 7 Основи теорії напруженого і деформованого стану твердого тіла проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р.
 ЗМІСТ ЛЕКЦІЇ q Розділ 3. Основи теорії напруженого і деформованого стану твердого тіла Ø 3. 6 Головні напруження. Інваріанти напруженого стану Ø 3. 7 Пряма і обернена задачі теорії напруженого стану в точці Ø 3. 8 Плоский напружений стан проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 2
ЗМІСТ ЛЕКЦІЇ q Розділ 3. Основи теорії напруженого і деформованого стану твердого тіла Ø 3. 6 Головні напруження. Інваріанти напруженого стану Ø 3. 7 Пряма і обернена задачі теорії напруженого стану в точці Ø 3. 8 Плоский напружений стан проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 2
 3. 6 Головні напруження. Інваріанти напруженого стану Можна довести, що через будь-яку точку тіла можна провести такі три взаємноперпендикулярні площадки, на яких будуть відсутні дотичні напруження, а з трьох нормальних напружень одне буде максимальним і одне – мінімальним. Площадки, на яких відсутні дотичні напруження, називаються головними площадками, а діючі на них нормальні напруження називаються головними напруженнями. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 3
3. 6 Головні напруження. Інваріанти напруженого стану Можна довести, що через будь-яку точку тіла можна провести такі три взаємноперпендикулярні площадки, на яких будуть відсутні дотичні напруження, а з трьох нормальних напружень одне буде максимальним і одне – мінімальним. Площадки, на яких відсутні дотичні напруження, називаються головними площадками, а діючі на них нормальні напруження називаються головними напруженнями. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 3
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Якщо головна площадка існує, то в ній : Тоді проекції повного напруження на координатні вісі дорівнюють: Підставивши ці значення до рівнянь рівноваги на поверхні тіла, одержимо наступну систему однорідних рівнянь відносно невідомих l, m, n: ( ) проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 4
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Якщо головна площадка існує, то в ній : Тоді проекції повного напруження на координатні вісі дорівнюють: Підставивши ці значення до рівнянь рівноваги на поверхні тіла, одержимо наступну систему однорідних рівнянь відносно невідомих l, m, n: ( ) проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 4
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Нульові розв’язки отриманої системи неможливі внаслідок відомого співвідношення між напрямними косинусами: ( ) Однорідна система рівнянь має розв’язки, відмінні від нуля лише за умови, якщо детермінант (визначник), складений з коефіцієнтів при l, m, n, перетворюється на нуль, тобто: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 5
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Нульові розв’язки отриманої системи неможливі внаслідок відомого співвідношення між напрямними косинусами: ( ) Однорідна система рівнянь має розв’язки, відмінні від нуля лише за умови, якщо детермінант (визначник), складений з коефіцієнтів при l, m, n, перетворюється на нуль, тобто: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 5
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Розкриваючи визначник, одержуємо рівняння третього ступеню відносно невідомого головного напруження σn: Після спрощення даного виразу одержимо наступне кубічне рівняння: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 6
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Розкриваючи визначник, одержуємо рівняння третього ступеню відносно невідомого головного напруження σn: Після спрощення даного виразу одержимо наступне кубічне рівняння: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 6
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Коефіцієнти називаються інваріантами напруженого стану в точці, так як вони незмінюють своєї величини при зміні орієнтації початкової системи прямокутних координат. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 7
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Коефіцієнти називаються інваріантами напруженого стану в точці, так як вони незмінюють своєї величини при зміні орієнтації початкової системи прямокутних координат. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 7
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Можна довести, що всі три кореня кубічного рівняння є дійсними. Це дозволяє вважати, що в кожній точці тіла, незалежно від його форми і розмірів, місця прикладання, виду і характеру навантажень, існує не більше трьох взаємноортогональних головних напружень σ1>σ2>σ3. Для визначення положення головної площадки необхідно знати напрямні косинуси нормалі до цієї площадки. Для їх визначення необхідно підставити знайдені головні напруження σ1, σ2, σ3 до будь-яких двох рівнянь системи ( ). Третім необхідним рівнянням є геометричне співвідношення ( ). проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 8
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Можна довести, що всі три кореня кубічного рівняння є дійсними. Це дозволяє вважати, що в кожній точці тіла, незалежно від його форми і розмірів, місця прикладання, виду і характеру навантажень, існує не більше трьох взаємноортогональних головних напружень σ1>σ2>σ3. Для визначення положення головної площадки необхідно знати напрямні косинуси нормалі до цієї площадки. Для їх визначення необхідно підставити знайдені головні напруження σ1, σ2, σ3 до будь-яких двох рівнянь системи ( ). Третім необхідним рівнянням є геометричне співвідношення ( ). проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 8
 3. 6 Головні напруження. Інваріанти напруженого стану, продовження Інваріанти напруженого стану можна записати через головні напруження: Тензор напружень через головні напруження записується так: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 9
3. 6 Головні напруження. Інваріанти напруженого стану, продовження Інваріанти напруженого стану можна записати через головні напруження: Тензор напружень через головні напруження записується так: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 9
 3. 6 Головні напруження. Інваріанти В напруженого стану, продовження головних напруженнях : В деяких випадках інваріанти можуть приймати нульове значення. Наприклад, якщо I 3=0, це означає, що один із коренів кубічного рівняння теж дорівнює нулю. В цьому випадку кажуть, що напруженний стан є двовісним або плоским. Якщо одночасно дорівнюють нулю другий та третій інваріанти тензора напружень (I 2=I 3=0), то маємо два нульових кореня і тільки одне головне напруження відмінне від нуля. Напружений стан в цьому випадку зветься одновісним або лінійним. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 10
3. 6 Головні напруження. Інваріанти В напруженого стану, продовження головних напруженнях : В деяких випадках інваріанти можуть приймати нульове значення. Наприклад, якщо I 3=0, це означає, що один із коренів кубічного рівняння теж дорівнює нулю. В цьому випадку кажуть, що напруженний стан є двовісним або плоским. Якщо одночасно дорівнюють нулю другий та третій інваріанти тензора напружень (I 2=I 3=0), то маємо два нульових кореня і тільки одне головне напруження відмінне від нуля. Напружений стан в цьому випадку зветься одновісним або лінійним. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 10
 3. 7 Пряма і обернена задачі теорії напруженого стану в точці В теорії напруженого стану можна виділити дві основні задачі: пряму та обернену. Пряма задача. В точці тіла відомі положення головних площадок і значення головних напружень. Треба знайти нормальні та дотичні напруження, які діють на довільній площадці, положення якої відносно головних площадок відомо. Обернена задача. В деякій точці тіла відомі нормальні та дотичні напруження, які діють на трьох взаємноперпендикулярних площадках, що проходять через дану точку. Треба знайти положення головних площадок та значення головних напружень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 11
3. 7 Пряма і обернена задачі теорії напруженого стану в точці В теорії напруженого стану можна виділити дві основні задачі: пряму та обернену. Пряма задача. В точці тіла відомі положення головних площадок і значення головних напружень. Треба знайти нормальні та дотичні напруження, які діють на довільній площадці, положення якої відносно головних площадок відомо. Обернена задача. В деякій точці тіла відомі нормальні та дотичні напруження, які діють на трьох взаємноперпендикулярних площадках, що проходять через дану точку. Треба знайти положення головних площадок та значення головних напружень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 11
 3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання прямої задачі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 12
3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання прямої задачі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 12
 3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання оберненої задачі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 13
3. 7 Пряма і обернена задачі теорії напруженого стану в точці, продовження Розв’язання оберненої задачі: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 13
 3. 8 Плоский напружений стан Досліджуючи напружений стан елементів конструкцій, найчастіше доводиться мати справу з плоским напруженим станом. Плоский напружений стан, наприклад, виникає у тонкостінних пластинках, на які діють зусилля розташовані у серединній площині. • • Плоский напружений стан також має місце на поверхні деталі або елемента конструкції, яка вільна від зовнішніх навантажень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 14
3. 8 Плоский напружений стан Досліджуючи напружений стан елементів конструкцій, найчастіше доводиться мати справу з плоским напруженим станом. Плоский напружений стан, наприклад, виникає у тонкостінних пластинках, на які діють зусилля розташовані у серединній площині. • • Плоский напружений стан також має місце на поверхні деталі або елемента конструкції, яка вільна від зовнішніх навантажень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 14
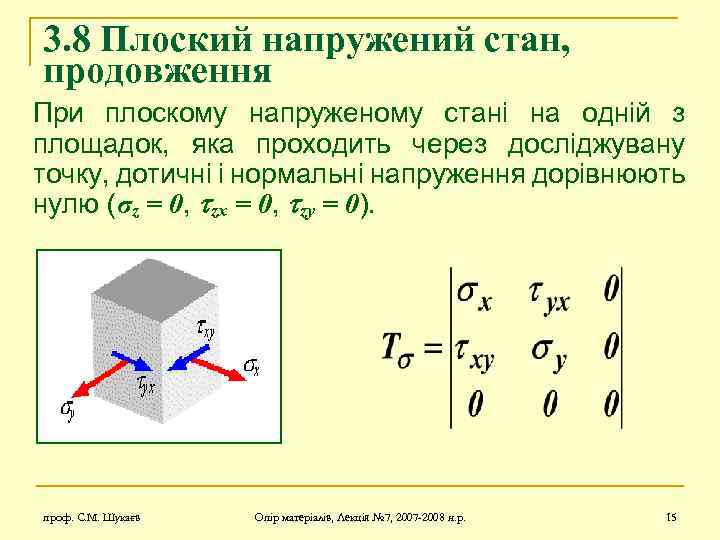 3. 8 Плоский напружений стан, продовження При плоскому напруженому стані на одній з площадок, яка проходить через досліджувану точку, дотичні і нормальні напруження дорівнюють нулю (σz = 0, zx = 0, zy = 0). проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 15
3. 8 Плоский напружений стан, продовження При плоскому напруженому стані на одній з площадок, яка проходить через досліджувану точку, дотичні і нормальні напруження дорівнюють нулю (σz = 0, zx = 0, zy = 0). проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 15
 3. 8 Плоский напружений стан, продовження Головні напруження визначаються з рівняння: В результаті розв’язання даного рівняння отримаємо: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 16
3. 8 Плоский напружений стан, продовження Головні напруження визначаються з рівняння: В результаті розв’язання даного рівняння отримаємо: проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 16
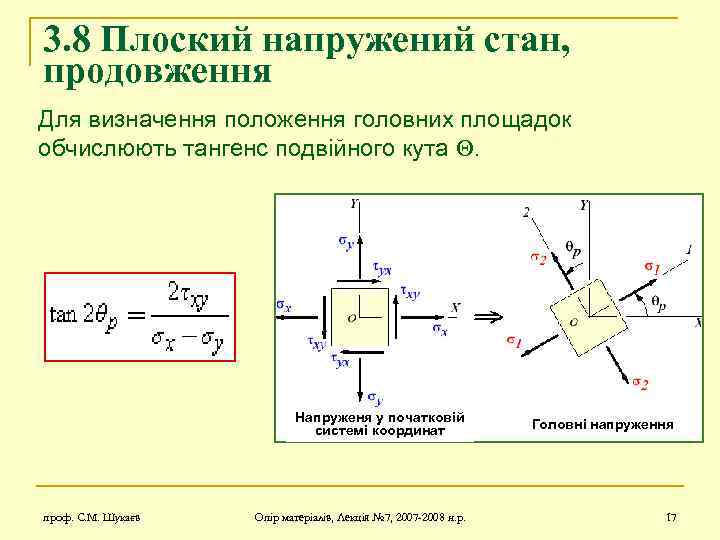 3. 8 Плоский напружений стан, продовження Для визначення положення головних площадок обчислюють тангенс подвійного кута . Напруженя у початковій системі координат проф. С. М. Шукаєв Головні напруження Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 17
3. 8 Плоский напружений стан, продовження Для визначення положення головних площадок обчислюють тангенс подвійного кута . Напруженя у початковій системі координат проф. С. М. Шукаєв Головні напруження Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 17
 ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 18
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 7, 2007 -2008 н. р. 18


