ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція - 6 Основи теорії напруженого і деформованого стану твердого тіла
ЗМІСТ ЛЕКЦІЇ q Ø Ø Ø Розділ 3. Основи теорії напруженого і деформованого стану твердого тіла 3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) 3. 4 Закон парності дотичних напружень 3. 5 Визначення напружень на довільній площадці проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 2
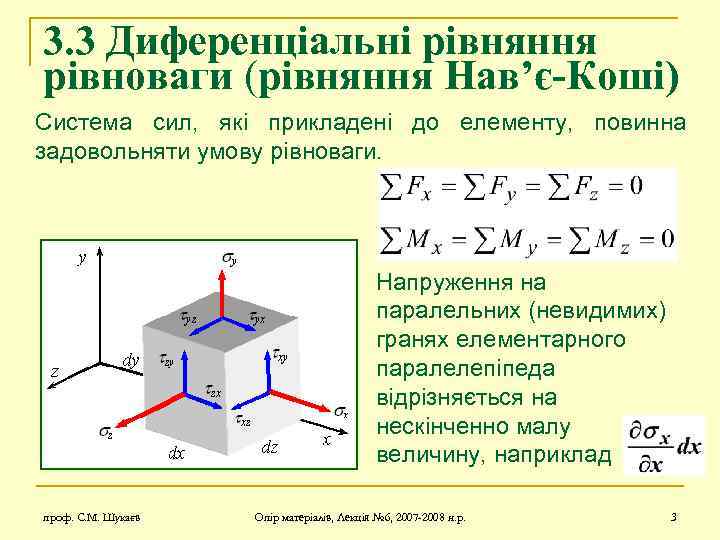3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) Система сил, які прикладені до елементу, повинна задовольняти умову рівноваги. Напруження на паралельних (невидимих) гранях елементарного паралелепіпеда відрізняється на нескінченно малу величину, наприклад проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 3
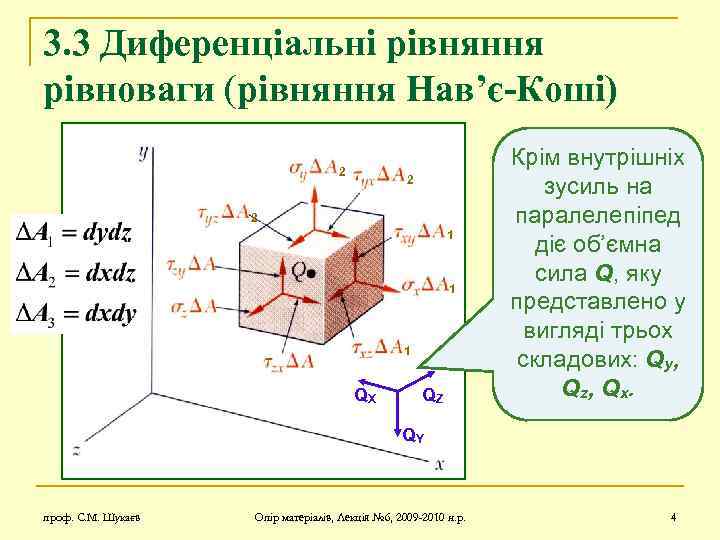3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) 2 2 2 1 3 1 3 QX QZ Крім внутрішніх зусиль на паралелепіпед діє об’ємна сила Q, яку представлено у вигляді трьох складових: Qy, Qz, Qx. QY проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2009 -2010 н. р. 4
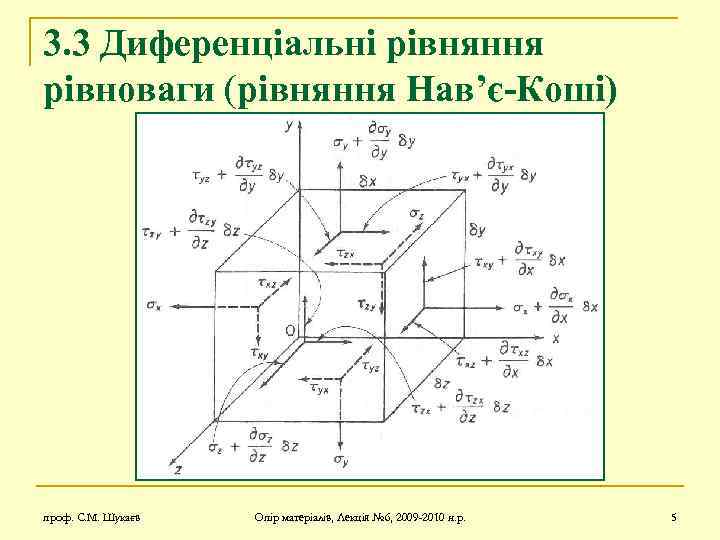3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2009 -2010 н. р. 5
3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) Складаємо рівняння рівноваги для виділеного елемента. Записуємо перше рівняння: Після спрощення, маємо: проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 6
3. 3 Диференціальні рівняння рівноваги (рівняння Нав’є-Коші) Аналогічно записуємо два наступних рівняння та отримуємо: Дана система рівнянь зветься диференціальними рівняннями рівноваги або рівняннями Нав’є-Коші. проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 7
3. 4 Закон парності дотичних напружень Складаємо рівняння рівноваги моментів відносно осі x: Аналогічно складаємо рівняння рівноваги відносно осей y та z. Нехтуючі складовими більш високого порядку малості, отримуємо: Одержані співвідношення звуться законом парності або взаємності дотичних напружень проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 8
3. 4 Закон парності дотичних напружень, продовження Закон взаємності дотичних напружень можна сформулювати таким чином: дотичні напруження, які виникають на двох взаємно перпендикулярних елементарних площадках, є рівними за величиною і направлені до або від ребра, що утворюється в результаті перетину елементарних площадок. Звідси випливає, що тензор напруження є симетричним, тобто компоненти, які розташовані симетрично відносно головної діагоналі (σx, σy, σz), рівні між собою. Таким чином, маємо не дев’ять, а тільки шість незалежних компонент тензора напружень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 9
3. 5 Визначення напружень на довільній площадці Доведемо наступне твердження: якщо відомо 6 компонент тензора напружень, а саме σx, σy, σz, xy, yz, zx, що діють на трьох взаємно перпендикулярних площадках, проведених навколо досліджуваної точки, то можна визначити напруження на будь-якій площадці, що проходить через цю точку. Для доведення цього положення виділимо з напруженого тіла елементарний чотирьохгранник (тетраедр), три грані якого перпендикулярні координатним осям, четверта грань являє собою похилу площину, проведену таким чином, що вона відсікає на ортогональних ребрах відрізки dx, dy, dz. проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 10
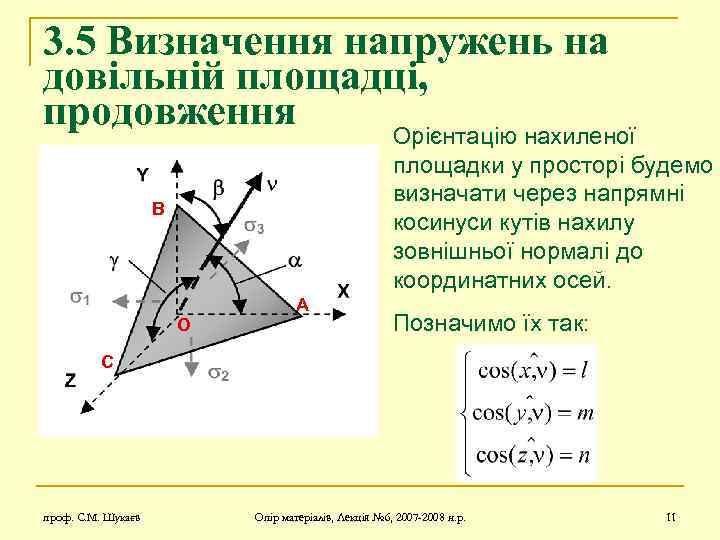3. 5 Визначення напружень на довільній площадці, продовження Орієнтацію нахиленої площадки у просторі будемо визначати через напрямні косинуси кутів нахилу зовнішньої нормалі до координатних осей. B O A Позначимо їх так: C проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 11
3. 5 Визначення напружень на довільній площадці, продовження Між направляючими косинусами існує наступний зв’язок: Площу трикутника АВС позначимо через A, площу трикутника ОВС – Ax, площу трикутника ОАС – Ay, площу трикутника ОВА – Az. Очевидно, що: проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 12
3. 5 Визначення напружень на довільній площадці, продовження Позначимо проекції повного напруження на площадці АВС через Px, Py, Pz. Складаємо рівняння рівноваги тетраедра. Для чого множимо кожне напруження на площу відповідної грані, щоб перейти від напружень до сил. В результаті цих дій одержуємо наступне рівняння: Аналогічно отримаємо два інші рівняння: проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 13
3. 5 Визначення напружень на довільній площадці, продовження Одержана система рівнянь дозволяє для будь-якої площадки, орієнтацію якої в просторі визначають косинуси l, m, n, визначити проекції повного напруження Px, Py, Pz через компоненти тензора напружень. Якщо нахилена площадка є частиною поверхні тіла, то дані рівняння уявляють собою граничні умови і звуться рівняннями (умовами) рівноваги на поверхні тіла. Повне напруження на нахиленій площадці визначається таким чином: проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 14
3. 5 Визначення напружень на довільній площадці, продовження Проекція повного напруження на нормаль дорівнює Дотична складова повного напруження: проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 15
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 6, 2007 -2008 н. р. 16