ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція – 13 Кручення стержнів
ЗМІСТ ЛЕКЦІЇ q Розділ n n 5. Кручення. 5. 3 Кручення тонкостінних стержнів з незамкненим профілем. 5. 4 Кручення тонкостінних стержнів з замкненим профілем. 5. 5 Про раціональну форму перерізу стержня при крученні 5. 6 Розрахунок гвинтових циліндричних пружин. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 2
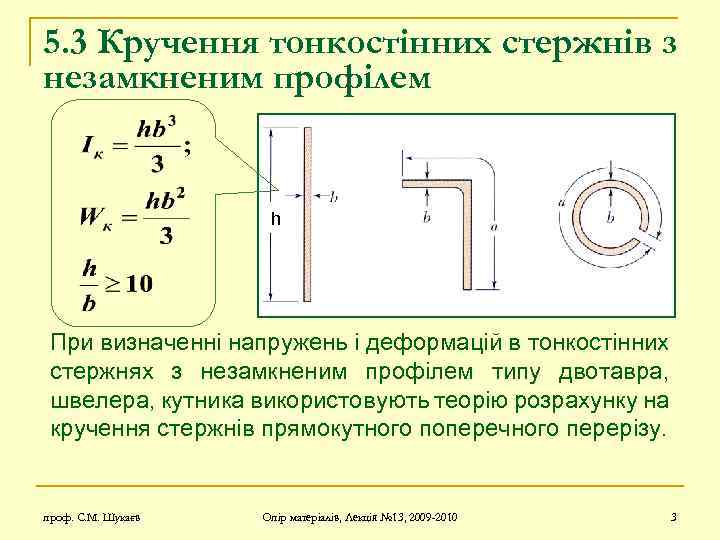5. 3 Кручення тонкостінних стержнів з незамкненим профілем h При визначенні напружень і деформацій в тонкостінних стержнях з незамкненим профілем типу двотавра, швелера, кутника використовують теорію розрахунку на кручення стержнів прямокутного поперечного перерізу. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 3
5. 3 Кручення тонкостінних стержнів з незамкненим профілем 1 Розглянемо тонкостінний переріз стержня. Розбиваємо переріз на n тонкостінних елементів у вигляді прямокутників. Для всього стержня момент інерції 2 де 3 - значення моменту інерції для і-го елементу. Момент опору при крученні де проф. С. М. Шукаєв - розмір меншої сторони прямокутного елементу, що має найбільшу товщину. Опір матеріалів, Лекція № 13, 2009 -2010 4
5. 3 Кручення тонкостінних стержнів з незамкненим профілем Найбільші дотичні напруження виникають посередині найдовших сторін елемента що має найбільшу товщину. При цьому tмах – максимальна товщина елементу. Кут закручування визначається за формулою: В розрахунках на кручення прокатних профілів величину Jk помножують на коефіцієнт, який має наступні значення: 1 – кутовий переріз; 1, 2 – двотавровий переріз; 1, 15 – тавровий переріз; 1, 12 – швелер. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 5
5. 4 Кручення тонкостінних стержнів з замкненим профілем Розглядаючи кручення стержня з замкненим тонкостінним профілем, будемо вважати товщину стінки стержня настільки малою, що дотичні напруження до неї можна прийняти однаковими та рівними напруженням, що діють посередині товщини стінки і направлені по дотичній до серединної лінії. Двома поперечними перетинами, відстань між якими x і двома довільними перетинами вздовж осі стержня виділимо елемент. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 6
5. 4 Кручення тонкостінних стержнів з замкненим профілем Спроектуємо всі сили на вісь Х: Таким чином, добуток дотичного напруження на товщину перерізу є сталою величиною для будь-якої точки поперечного перерізу. Цей добуток t зветься потоком напружень. Отже, найбільше дотичне напруження виникає там, де товщина мінімальна і навпаки. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 7
5. 4 Кручення тонкостінних стержнів з замкненим профілем Для того, щоб зв’язати потік дотичних напружень з моментом кручення, який діє на стержень, розглянемо елемент довжиною ds, який лежить в поперечному перерізі. d. A A проф. С. М. Шукаєв Момент сили tds відносно довільної точки О. - формула Бредта. Опір матеріалів, Лекція № 13, 2009 -2010 8
5. 5 Раціональна форма поперечного перерізу при крученні З усіх перерізів, що мають однакові моменти опору кручення, раціональним буде переріз, який має найменшу площу, тобто забезпечує найменшу кількість матеріалу при заданому моменті опору кручення. Раціональність форми поперечного перерізу звичайно оцінюється питомим моментом опору: , де А – площа перерізу. Найбільш раціональними є тонкостінні замкнені перерізи, які мають найбільше значення ωк, а найменш раціональними є тонкостінні незамкнені перерізи. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 9
5. 6 Розрахунок гвинтових циліндричних пружин Гвинтові пружини – це найпоширеніший тип пружин. Найчастіше їх виробляють із дроту круглого поперечного перерізу. При великих зовнішніх навантаженнях застосовуються пружини із витками квадратного та прямокутного перерізу, які вирізаються із трубчастих заготовок. Точний розрахунок на міцність гвинтової циліндричної пружини є досить складним, оскільки дріт пружини може одночасно зазнавати кручення, зсув та згинання. Але при малих кутах нахилу витків ( біля 10 -12 градусів) впливом згинання можна знехтувати, що спрощує розрахунок. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 10
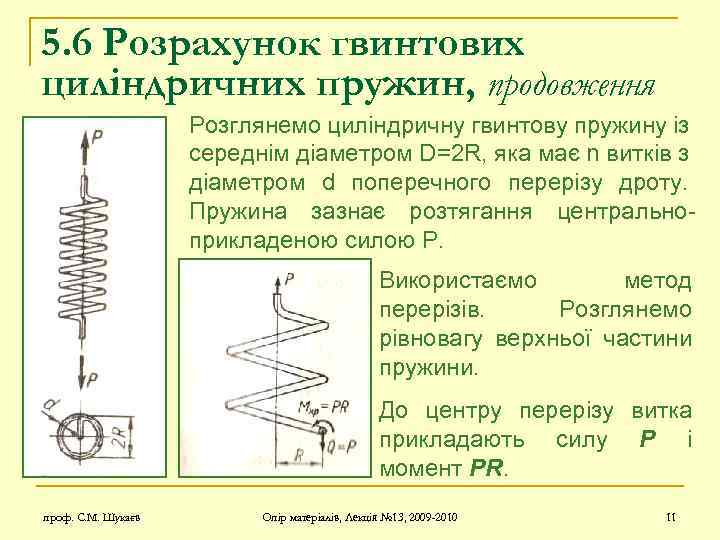5. 6 Розрахунок гвинтових циліндричних пружин, продовження Розглянемо циліндричну гвинтову пружину із середнім діаметром D=2 R, яка має n витків з діаметром d поперечного перерізу дроту. Пружина зазнає розтягання центральноприкладеною силою Р. Використаємо метод перерізів. Розглянемо рівновагу верхньої частини пружини. До центру перерізу витка прикладають силу Р і момент PR. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 11
5. 6 Розрахунок гвинтових циліндричних пружин, продовження Покажемо розподілення напруження від зрізу і кручення: З аналізу розподілення напружень видно, що найбільш навантаженою точкою перерізу буде точка А. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 12
5. 6 Розрахунок гвинтових циліндричних пружин, продовження У розрахунках пружин великого діаметру складовою зсуву нехтують і враховують тільки напруження кручення. Тоді, умова міцності пружини з дроту круглого перерізу записується так: Крім розрахунку на міцність пружини розраховують на осадку, тобто визначають величину, на яку під дією прикладеного зусилля пружина може бути розтягнутою або стиснутою. Величина осадки позначається λ і розраховується за формулою: проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 13
6. Зсув. Розрахунок на зріз Деформація зсуву відбувається тоді, коли з шести компонент головного вектора сили та головного вектора моменту внутрішніх зусиль відмінні від нуля тільки поперечні сили На практиці зсув у чистому вигляді важко отримати, так як деформація зсуву звичайно супроводжується іншими видами деформації (найчастіше згином). проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 14
6. 1. Чистий Зсув У розрахунках ряду елементів конструкцій зустрічається випадок плоского напруженого стану, коли на чотирьох гранях прямокутного елементу діють тільки дотичні напруження. Такий напружений стан зветься чистим зсувом. Головні напруження при зсуві визначаються за формулами оберненої задачі проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 15
6. 2. Закон Гука при чистому зсуві Закон Гука при зсуві: дотичні напруження пропорційні кутовій деформації. Враховуючи, що закон Гука можна представити в іншому виді - закон Гука для абсолютного зсуву. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 16
6. 3. Розрахунок на міцність при зсуві (розрахунок на зріз) Умова міцності: – для пластичних матеріалів; – для крихких матеріалів. 6. 3. 1. Розрахунок заклепкових з’єднань Дано: сила Р; товщина листів ; кількість заклепок – n. Обчислити діаметр заклепок. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 17
6. 3. 1. Розрахунок заклепкових з’єднань, продовження Розрахунок заклепок на зріз: Якщо заклепки зрізаються по і площинах, тоді площа зрізу усіх заклепок Розрахунок заклепок і листів на зминання (наближений): З розрахунку на зріз і зминання вибирають більший діаметр. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 18
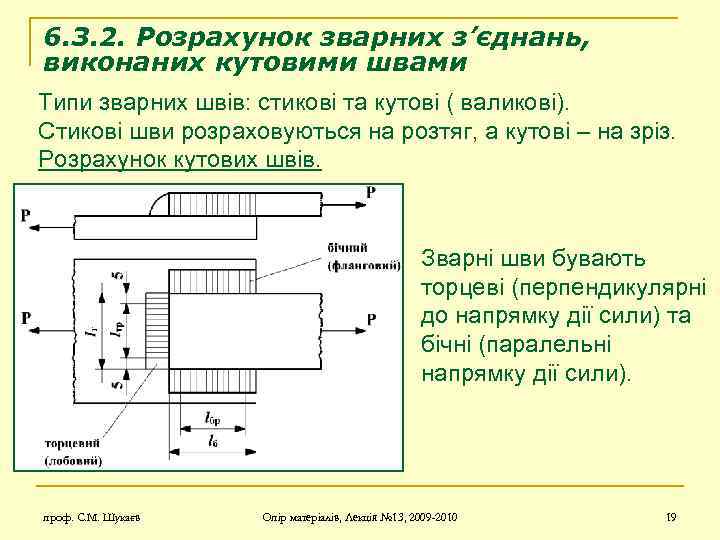6. 3. 2. Розрахунок зварних з’єднань, виконаних кутовими швами Типи зварних швів: стикові та кутові ( валикові). Стикові шви розраховуються на розтяг, а кутові – на зріз. Розрахунок кутових швів. Зварні шви бувають торцеві (перпендикулярні до напрямку дії сили) та бічні (паралельні напрямку дії сили). проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 19
6. 3. 2. Розрахунок зварних з’єднань, виконаних кутовими швами Вважаючи, що шов зрізається по його мінімальному поперечному перерізу, одержимо розрахункову площу зрізу k – катет шва. – розрахункова, а - фактична довжина шва, 10 мм враховує непровар шва з двох його кінців. Умова міцності одного шва: - допустиме напруження для зварних швів. проф. С. М. Шукаєв Опір матеріалів, Лекція № 13, 2009 -2010 20
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 14, 2008 -2009 21