ОПІР МАТЕРІАЛІВ Семестр - 1 Лекція – 11 Розрахунки на міцність. Критерії міцності проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009
ЗМІСТ ЛЕКЦІЇ q Розділ 4. Розрахунки на міцність. Критерії міцності Ø 4. 1 Методи розрахунків. Ø 4. 2 Призначення теорій міцності Ø 4. 3 Класичні теорії міцності проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 2
4. 1 Методи розрахунків Після визначення всіх компонент напруженого і деформованого стану необхідно дати оцінку одержаних величин з точки зору безпечності роботи конструкції, тобто оцінити міцність і жорсткість конструкції. 4. 1. 1 УМОВИ ЖОРСТКОСТІ. Нагадаємо, що під жорсткістю розуміють здатність конструкції та її елементів протистояти зовнішнім навантаженням, не змінюючи форми і розмірів. Жорсткість конструкції оцінюється шляхом порівняння отриманих максимальних переміщень із нормативними значеннями. Для конкретних деформацій умови міцності записуються так: umax uгр fmax fгр φmax φгр проф. С. М. Шукаєв – для осьових деформацій; – для згинання; – для кручення. Опір матеріалів, Лекція № 10, 2008 -2009 Розрахунки на жорсткість завжди доповнюють розрахунками на міцність! 3
4. 1 Методи розрахунків, продовження 4. 1. 2 УМОВИ МІЦНОСТІ Найважливішим завданням інженерного розрахунку є оцінка міцності елементів машин і споруд за відомим напруженим станом. Найпростіше ця задача розв'язується для простих видів деформації (розтягання, кручення) оскільки в цих випадках граничні (небезпечні) напруження можуть бути визначені безпосередньо з експерименту. Небезпечним вважають напруження, при якому починається руйнування (у крихкому стані матеріалу) або з'являються залишкові деформації (у пластичному стані матеріалу). За небезпечним напруженням визначають допустиме напруження. Коефіцієнт запасу проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 4
4. 2 Призначення теорій міцності При складному напруженому стані (плоскому або об'ємному) немає однозначної відповіді на питання, яке напруження необхідно брати для перевірки міцності. Експерименти показують, що руйнування відбуваються при різних співвідношеннях головних напружень. Крім того, встановлено, що напружений стан впливає на механічні характеристики матеріалу. Для того, щоб уникнути складних випробувань, використовують випробування стандартних зразків матеріалу і роблять на цій основі узагальнення. Найбільш доречно робити це шляхом заміни складного напруженого стану еквівалентним йому одновісним. Для цього використовується метод побудови за трьома головними напруженнями чинника, за яким можна оцінити міцність. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 5
4. 2 Призначення теорій міцності, продовження За довільного напружено-деформованого стану тіла граничний стан досягається після досягнення цим чинником або певною комбінацією таких чинників деякого критичного значення. Вибір визначальних для руйнування чинників називають механічною теорією міцності, а математичний запис умови досягнення згаданими чинниками критичного значення - критерієм (умовою) руйнування. Призначенням теорій міцності є прогнозування міцності (граничного стану) тіл у складному напруженому стані на основі узагальнення результатів вивчення граничного стану за найпростіших способів навантажування. Існує велика кількість теорій міцності. Найбільш розповсюдженими є п’ять теорій міцності, які іноді називають класичними. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 6
4. 3 Класичні теорії міцності 4. 3. 1 Теорія найбільших нормальних напружень Згідно з цією теорією небезпечний стан у точці тіла виникає тоді, коли найбільше за модулем головне напруження досягає граничного значення, що є характеристикою матеріалу: Теорія запропонована Галілео Галілеєм. Пізніше її використовували Лейбніц, Ляме, Клебш та Ренкін. Під іменем останнього теорія відома в англо-американській літературі, у російській її називають першою класичною теорією міцності. Ізотропний матеріал навіть за дуже великого рівномірного всебічного стиску не руйнується. Тому одним із недоліків теорії є твердження, що за одновісного розтягання границя міцності така сама, як і за всебічного стискання. Перша теорія міцності експерементально підтверджується лише для крихких матеріалів. Використовується рідко, бо не враховує двох головних напружень. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 7
4. 3 Класичні теорії міцності, продовження 4. 3. 2 Теорія найбільших лінійних деформацій Згідно з цією теорією руйнування в умовах багатовісного напруженого стану відбуваються тоді, коли максимальна головна лінійна деформація досягає або перевищує значення максимальної лінійної деформації, що відповідає границі текучості або границі міцності. Застосування другої теорії міцності неприпустимо за межами дії закону Гука або за межами пропорційності. Дослідна перевірка цієї теорії вказує на узгодження результатів лише для крихкого стану матеріалу. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 8
Maximum Shear Stress Criterion (Tresca Criterion) The theory of maximum shear stress proposed by Coulomb (1773) became widely known owing to the experiments performed by Tresca and Bauschinger. The maximum shear stress theory is based on yielding, thus you can only use it for ductile materials. The theory states that failure (i. e. , critical state which prevents operational loading) occurs when the maximum shear stress in the complex stress system becomes equal to that at the yield point in the tensile test. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 9
Maximum Shear Stress Criterion, continued According to this theory, the yield strength in shear is half of the normal yield strength. The maximum shear stress is Thus the maximum shear stress theory predicts that failure will occur whenever проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 10
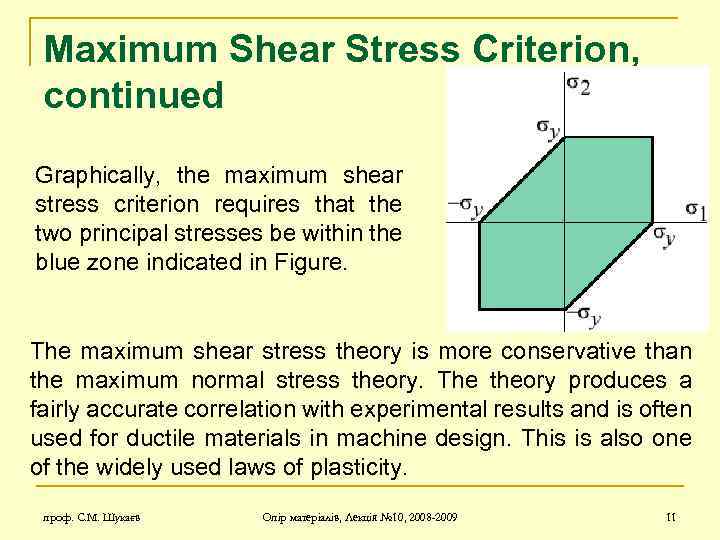Maximum Shear Stress Criterion, continued Graphically, the maximum shear stress criterion requires that the two principal stresses be within the blue zone indicated in Figure. The maximum shear stress theory is more conservative than the maximum normal stress theory. The theory produces a fairly accurate correlation with experimental results and is often used for ductile materials in machine design. This is also one of the widely used laws of plasticity. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 11
Maximum distortion energy criterion (Von Mises Criterion) The von Mises Criterion (1913), also known as the maximum distortion energy criterion, octahedral shear stress theory, or Maxwell-Huber-Hencky-von Mises theory, is often used to estimate the yield of ductile materials. This theory, based on determination of the distortion energy in a given material, i. e. , of the energy associated with changes in shape (as opposed to the energy associated with changes in volume) states that failure occurs when the maximum distortion energy component in a complex stress system becomes equal to that at the yield point in the tensile test. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 12
Maximum distortion energy criteria (Von Mises Criterion) Distortion energy per unit volume Ud is less than that occurring in a tensile test specimen at yield Udy. in the case of general stress state, is For the simple tension test, Therefore the distortion energy is проф. С. М. Шукаєв and Опір матеріалів, Лекція № 10, 2008 -2009 . 13
Von Mises Criterion, continued Substituting the above-presented relations in the limit condition gives A circular cylinder equally tilted to the axes, which is described around Coulomb's prism, corresponds to the distortion energy theory in a stress space. This theory has received considerable verification in practice and is widely regarded as the most reliable basis for design. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 14
Критерій Мора ґрунтується на припущенні, що міцність матеріалів у загальному випадку напруженого стану залежить в основному від значення і знака найбільшого 1 та найменшого 3 головних напружень. При =1 (пластичні матеріали) критерій збігається з критерієм найбільших дотичних напружень. Недолік критерію – не враховує вплив 2. Область використання -- крихкі матеріали. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 15
Нові критерії міцності. Критерій Писаренка-Лебедєва Представником нових критеріїв міцності, запропонованих, в основному, для крихких матеріалів, є критерій Писаренка-Лебедєва де i - інтенсивність напружень, i = IV; Для пластичних матеріалів =1 і критерій збігається з критерієм IV теорії міцності Для крихких матеріалів і критерій збігається з критерієм I теорії міцності Область використання – крихкі матеріали. проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 16
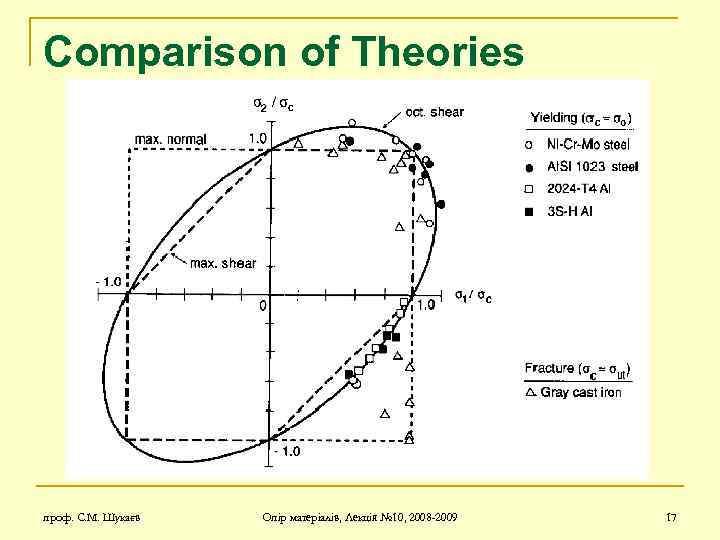Comparison of Theories проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 17
ДЯКУЮ ЗА УВАГУ! проф. С. М. Шукаєв Опір матеріалів, Лекція № 10, 2008 -2009 18