Операторы симметрии трехмерного континуума Расположение элементов симметрии

Операторы симметрии трехмерного континуума

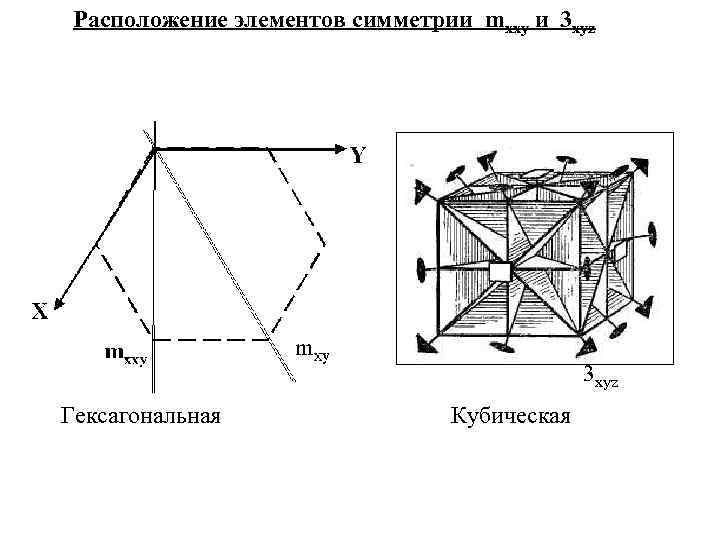Расположение элементов симметрии mxxy и 3 xyz Гексагональная Кубическая

Точечная группа симметрии – это серии последовательно реализуемых независимых операторов симметрии. Независимым (для данной точечной группы) является оператор, который сам по себе не есть произведение двух других, входящих в рассматриваемую точечную группу. Точечная группа 222 Ось 2 z является производной от осей 2 x и 2 y. Точечная группа mmm Все три плоскости независимы. В этой точечной группе все три оси симметрии 2 x, 2 y и 2 z являются производными от плоскостей зеркального отражения.

Точечные группы и генерирующие операторы Точечная группа Генерирующие независимые операторы Для генерации любой точечной группы симметрии нужно не более 3 х операторов.

Правильные системы точек (простые формы) точечной группы. Правильная система точек в точечной группе связана с простой формой, через проекцию конца нормали (точка) к граням простой формы. Кратность точки общего положения определяется произведением кратностей действующих в точечной группе независимых операторов. Пример: точечная группа 4 2=8 (m – производный элемент симметрии). Координаты правильной системы точек находят подстановкой координат исходной точки во все генерирующие операторы последовательно: +2 xz

Пространственная группа симметрии генерируется: 1. Независимыми операторами сходной точечной группы (41 cm 4 mm). 2. Компонентами трансляций действующих элементов симметрии (41 c/4; c c/2). 3. Группой трансляций Бравэ: P, C, I, F Правильная система точек общего положения, свойственная пространственной группе, получаются как правильная система точек сходной точечной группы, координаты которых почленно сложены с суммой компонентов трансляции этих операторов, а результат суммирован с группой трансляций Бравэ. Суммарные компоненты трансляций операторов зависят от выбора начала координат. Выбор начала координат зависит от, того к какой группе относится рассматриваемая пространственная группа. 230 пространственных групп состоят из: 1. 74 симморфных групп. 2. 54 гемисимморфных групп. 3. 103 семисимморфных групп.

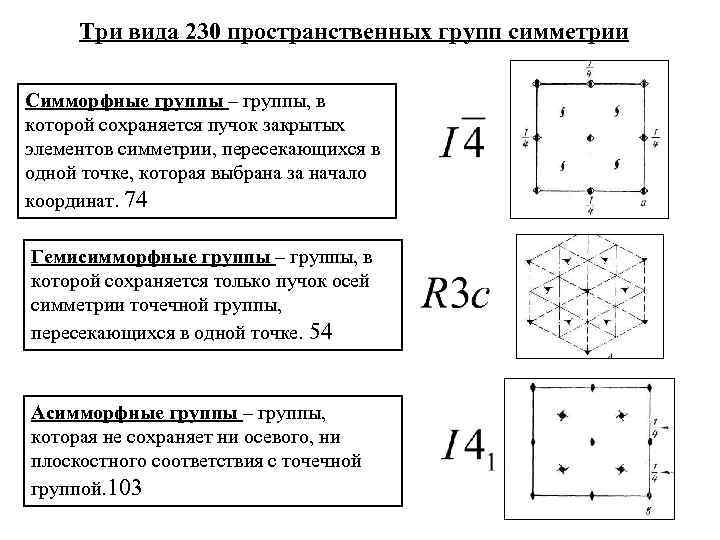Три вида 230 пространственных групп симметрии Симморфные группы – группы, в которой сохраняется пучок закрытых элементов симметрии, пересекающихся в одной точке, которая выбрана за начало координат. 74 Гемисимморфные группы – группы, в которой сохраняется только пучок осей симметрии точечной группы, пересекающихся в одной точке. 54 Асимморфные группы – группы, которая не сохраняет ни осевого, ни плоскостного соответствия с точечной группой. 103

Правильные системы точек симморфных групп симметрии (начало координат совпадает с точкой пересечения генерируюших операторов) Правильные системы точек симморфных групп определяют только из операторов сходственных точечных групп, а размножают трансляционной группой Бравэ. Система точек удовлетворяющая оператору Размножаем базисом I (000; 1/2 ½) : ½+x ½+y ½+z; ½+y ½ -x ½-z; ½-x ½-y ½+z; ½-y ½ +x ½-z Правильная система точек общего положения кратностью 8.

Правильные системы точек гемисимморфных групп симметрии (начало координат выбирают в стороне от генерируюших операторов в точке максимальной симметрии. Величина симметрии определяется разностью кратностей точек общего положения и того положения, величину симметрии которого определяют) Правильные системы точек гемисимморфных групп определяют из операторов сходственных точечных групп, компонентов трансляции связанной с ними и группой Бравэ. 3 z c R Правильная система точек общего положения кратностью 12.

Правильные системы точек асимморфных групп симметрии (начало координат асимморфных групп выбирают также как и для гемисимморфных групп). Отличие заключается в том, что компоненты трансляций собственно оператора суммируют с компонентами выноса оператора от начала координат. Оператор 4 относят к точке (x-¼, y-¼, z) и с учетом собственной трансляции оператора 41 (0, 0, 1/4) получают точки: (x-¼, y-¼, z); (y-¼, x-¼, z+¼); (¼-x, ¼-y, z+ 2/4); (¼-y, ¼-x, z+¾). После возвращения к старому началу координат получаем: (x, y, z); (y, ½-x, z+¼); (½-x, ½-y, z+½); (½-y, ½-x, z+¾ ). Добавление группы Бравэ I (000; 1/2, 1/2) даст ещё четыре точки: (x+½, y+½, z+½+½); (y+½, -x, z+¾); (-x, -y, -z); (-y, x+½, z+¼ ). После приведения этой системы из 8 точек к виду с наименьшими дробными коэфициентами получают стандартную правильную систему точек группы Сумма собственных трансляций и трансляции выноса оператора: (0 1/2 1/4)