Операторы физических величин • В квантовой механике каждой

Операторы физических величин • В квантовой механике каждой физической величине F сопоставляется эрмитов оператор по следующему правилу: • где - среднее значение (математическое ожидание) величины F для системы, находящейся в состоянии с волновой функцией .

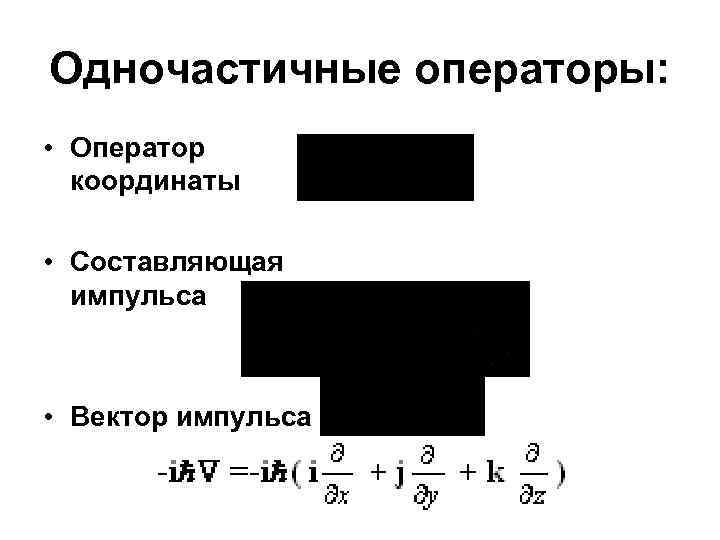Одночастичные операторы: • Оператор координаты • Составляющая импульса • Вектор импульса

Если физическая величина может быть записана в виде функции f от координат и импульса, то то есть в функции f импульс заменен на оператор

• Оператор Гамильтона для частицы с массой m строится по аналогии с функцией Гамильтона H • H = T+U(x, y, z, t) =

Оператор Гамильтона для системы частиц

Дифференцирование операторов по времени

Уравнение Шредингера

И производная оператора по времени имеет вид

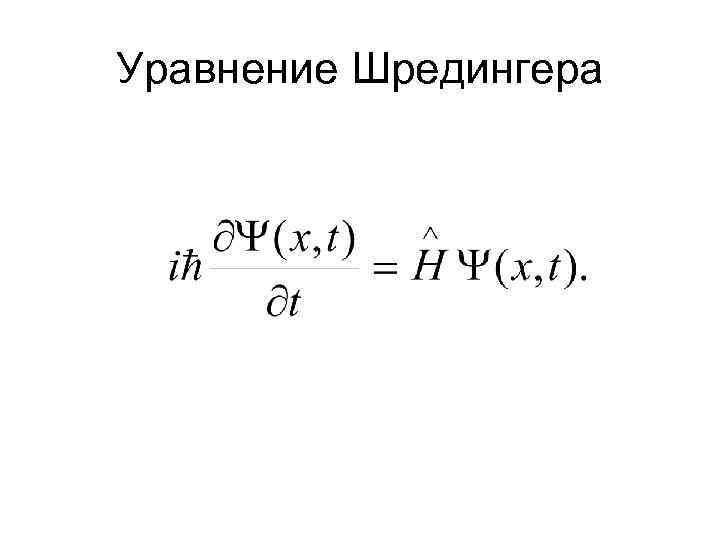Уравнение Шредингера

Стационарные состояния: гамильтониан не зависит от времени (x, t) = (x)·f(t)

Два уравнения : Е – это полная энергия системы.

Полная функция

Распределение электронной плотности для стационарных состояний не зависит от времени.

Задача • Общим решением уравнения Шредингера в случае стационарного состояния является произвольная линейная комбинация собственных функций Гамильтониана