OPERATIVNO PLANIRANJE PROCESA RUKOVANJA MATERIJALOM U INTRALOGISTICI OPERATIONAL

OPERATIVNO PLANIRANJE PROCESA RUKOVANJA MATERIJALOM U INTRALOGISTICI OPERATIONAL PLANNING OF MATERIALS HANDLING PROCESSES IN INTRALOGISTICS Milorad Vidović Kontakt: +381 11 3091 202 mvidovic@sf. bg. ac. yu Univerzitet u Beogradu, Saobraćajni fakultet

Plan izlaganja v Operativno planiranje v Rukovanje materijalom i operativno planiranje pogled unazad v Rukovanje materijalom i operativno planiranje – stanje o oblasti v Tipične formulacije i načini rešavanja problema Primeri v Problem povezivanja transportno manipulativno vozilo – zadatak – baterija v Plana rada kojim se minimizira ukupan broj pretovarnih sredstava koje treba angažovati v Plan alokacije pretovarnih postrojenja za istovar šljunka iz barži

Operativno planiranje v Pojam planiranja danas se primenjuje u gotovo svim govornim područjima i u praktično svim oblastima kao univerzalan pojam sa više značenja koja se uvek odnose na opis onoga što se čini sada, a usmereno je budućem v Dok se upravljanje može posmatrati kao proces realizacije planom utvrđenih aktivnosti, planiranje se može razumeti kao sofisticirana podloga tog procesa v Za razliku od strateškog operativno planiranje se odnosi na ciljeve i postupke tekućeg - "svakodnevnog" upravljanja procesima

Operativno planiranje… v Zadatak operativnog planiranja je stalno "usmeravanje" sistema ka željenom stanju kroz implementaciju postupaka kojima se sistem iz skupa različitih mogućih stanja dovodi u ono koje je najbliže ciljnom v U suštini, operativno planiranje podrazumeva procenu tekućeg, anticipaciju budućeg i izbor postupaka i jedne ili više aktivnosti kojima se sistem prevodi u stanje blisko željenom

Operativno planiranje… v Ukratko, reč je o primeni različitih metoda OI i postupaka za podršku odlučivanju, pri čemu je bitno imati na umu tesnu povezanost problema operativnog i taktičkog planiranja TAKTIČKO PLANIRANJE OPERATIVNO PLANIRANJE v U okvirima Intralogistike mogu se uočiti različite oblasti primene metoda operativnog planiranja – generalno to su: ü Skladišni procesi ü Sortirni procesi ü Procesi komisioniranja ü Procesi unutrašnjeg ü Kros dok procesi transporta. . .

Rukovanje materijalom i operativno planiranje – pogled unazad v Sa razvojem metoda operacionh istraživanja širila se i primena tih metoda na rešavanje različitih klasa problema u sve većem broju oblasti v U fundamentalnom delu koje se bavi sistemima rukovanja materijalom (Apple M. J. , 1972), kvantitativnoj analizi ovih sistema posvećeno je čitavo jedno poglavlje v Dakle, pre više od tri decenije, u vreme kada dobar deo metoda i tehnika koje se danas primenjuju ili nije bio poznat, ili je njihova primena bila u povoju, uočen je značaj OR u optimizaciji i rešavanju zadataka koji su prisutni u sistemima rukovanja materijalom

Rukovanje materijalom i operativno planiranje – stanje u oblasti v U težištu su problemi upravljanja automatski vodjenim vozilima (AGVS), što je i dominirajuća tema najvećeg dela radova ü ü ü broj vozila kao posledica strategije upravljanja radom flote rutiranje i rasporedjivanje vozila parkiranje menadžment baterijama prevencija kolizije vozila • Tanchoco J. M. A. , “Material Flow Systems in Manufacturing”, Chapman & Hall (1994) • Vis I. F. A. , “Survey of research in the design and control of automated guided vehicle systems”, European Journal of Operational Research 170 (2006) 677 -709

Rukovanje materijalom i operativno planiranje – stanje u oblasti. . . v Razvijaju se i druge primene ü problem rasporedjivanja kranova (Lieberman R. , Turksen I. , 1981; Daganzo C. , 1989; Peterkofsky R. , Daganzo C. , 1990; Bish, E. K. , 2003), ü problemi definisanja optimalne pozicije čekanja ASR sredstva, sekvenciranje i grupisanje prijemno otpremnih zahteva (Egbelu, Wu 1993; Hwang, Lin 1993; Elsayed, Lee 1996) ü problemi upravljačke strategije za tzv. multi-šatl sredstva, tj. sisteme sa više zahvatnih naprava (napr. Malmborg 2000) ü problemi dodeljivanja veza (berth planning), simultano dodeljivanje veza i pretovarnih sredstava, odnosno pretovarnih mesta u pomorskom i rečnom transportu (Lai K. K. , Shih K. , 1992; Lim A. , 1998; Imai A. , Nishimura E. , Papadimitriou S. , 2001; Imai A. , Nishimura E. , Papadimitriou S. , 2003; Vidović M. Vukadinović K. , 2006)

Rukovanje materijalom i operativno planiranje – stanje u oblasti. . . ü problemi rutiranja pretovarnih sredstava i vozila unutrašnjeg transporta (Kim, K. Y. , Kim, K. H. , 1999; Nishimura E. , Imai A. , Papadimitriou S. , 2005) ü ruting problemi u skladištu (Ratliff H. D. , Rosenthal A. S. , 1983; Petersen C. G. , 1997; Roodbergen K. J. , Koster R. , 2001; Roodbergen K. J. , Vis I. F. A, 2006) ü tovarenje transportnih sredstava, kontenera i paleta (Shields J. J, 1984; Saginal D. J. , Perakis A. N, 1989; Kim K. Y. , 1997; Dyckhoff H. , 1990).

Tipične formulacije i načini rešavanja problema v U najvećem delu, definisani problemi se uz manja ili veća prilagođenja formulišu u obliku nekog od tradicionalnih optimizacionih zadataka ili nekog od dobro poznatih problema kombinatorne optimizacije ü linearnog programiranja sa varijacijama (celobrojno, razlomljeno, stohastičko, parametarsko, transportni zadatak, . . . ) ü dinamičko programiranje ü nelinearno programiranje ü teorija grafova, mreža ü problem trgovačkog putnika, rutiranja ü problem raspoređivanja resursa, ü dodeljivanja, povezivanja, particioniranja skupova ü planinarskog ranca, pakovanja, . . . i sl.

Tipične formulacije i načini rešavanja problema. . . v Mogućnost primene optimizacionih postupaka ograničena je na probleme manjih dimenzija, pa se, mnogo češće, koriste tehnike čija primena za rezultat ima ne optimalno, već po pravilu zadovoljavajuće rešenje ü različite heurističke procedure ü u poslednje dve decenije i metaheuristike: “klasične” - genetski algoritmi, tehnika simuliranog kaljenja i tabu pretraživanje ü Novije metaheuristike: metod promenljivih sredina - Variable Neighbourhood Search (Hansen P. , Mladenović N. , 2001), koncept inteligencije grupe, tzv. Particle Swarm Optimization (Clerc M. , 2006), u okviru čega treba pomenuti Ant system (Dorigo M. , Stützle T. , 2004), Bee system (Lučić P. , Teodorović D. , 2002) ü koncept aproksimativnog rezonovanja "fuzzy logike", neuronske mreže, hibridne tehnike

Problem povezivanja transportno manipulativno vozilo – zadatak – baterija

Problem se svodi na pitanje formiranja “trojki” (i, j, k), zadatak-vozilo-baterija koje obezbedjuju realizaciju procesa uz minimalne troškove

Plan alokacije pretovarnih postrojenja za istovar šljunka iz barži Problem se može formulisati na sledeći način. Za dati skup istovarnih mesta (barži) odrediti najbolji način raspoređivanja pretovarnih postrojenja i sekvence realizacije zadataka, tako da ukupno vreme opsluge, koje uključuje i sva vremena čekanja, bude minimalno

On the problem v. Gravel distribution by inland water transportation v loading of gravel by a suction dredger into barges v transport of gravel to the ports or unloading locations v unloading of gravel by a handling facility v NUMBER OF HANDLING FACILITIES IS RELATIVELY SMALL

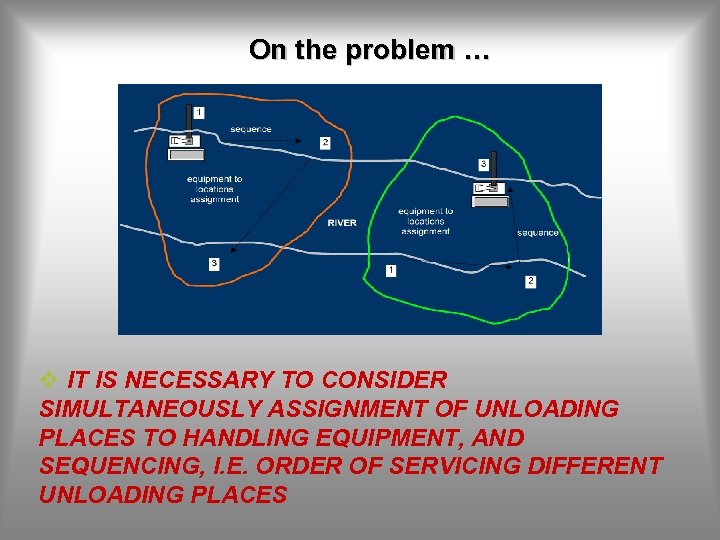On the problem … v IT IS NECESSARY TO CONSIDER SIMULTANEOUSLY ASSIGNMENT OF UNLOADING PLACES TO HANDLING EQUIPMENT, AND SEQUENCING, I. E. ORDER OF SERVICING DIFFERENT UNLOADING PLACES

Literature overview v. Related problems Ø First group of related problems covers fleet sizing and allocation problems Ø Beaujon and Turnquist, 1991 Ø Cheung and Powell, 1996 Ø Du and Hall, 1997 Ø Crainic, 2000 Ø Godfrey and Powell, 2002 a; Godfrey and Powell, 2002 b Ø Köchel at al. , 2003, . . . Ø approaches to solve the problems extend from linear and nonlinear network programming models via queuing theory models and dynamic programming models, approximation strategies for solving multistage stochastic allocation problems, to simulation, and evolutionary optimization - no closed-form solutions are available

Literature overview … Ø The second group of related problems are “the berth allocation problem”, i. e. “the berth planning (scheduling) problem” Ø Lai and Shih, 1992 Ø Lim, 1998 Ø Imai at al, 2001 Ø Nishimura at al, 2001 Ø Imai at al, 2003, Ø and “the crane assignment (scheduling) problem” Ø Daganzo, 1989 ØLim, 1998 ØPeterkofsky and Daganzo, 1990 ØBish, 2003 Øthe aim is to construct the berth schedule, and the calling schedule of vessels, while crane schedule covers crane assignment to vessels. - problems are mostly solved by heuristics

Berth allocation vs. gravel unloading problem ØVessel loading-unloading operations occupy berth, and cause delay of all other vessels waiting for berthing and service. Total delay for one vessel comprise loading-unloading time of all preceding vessels. ØSimilarly, in case of unloading gravel, a barge arrived waits for handling facility until all preceding barges are unloaded. ØWhile in case of the berth allocation problem, vessel transfer time may be neglected when compared with vessel loadingunloading time, handling facility transfer time between unloading places must be taken into consideration. ØThis fact increases problem complexity, and makes main difference between the berth allocation planning problems, and the gravel unloading problem studied here.

Problem formulation v FOR A GIVEN COLLECTION OF BARGES FIND A SET OF ASSIGNMENTS TO MINIMIZE THE SUM OF THE SERVICE TIMES INCLUDING WAITING FOR SERVICE AND HANDLING DEVICES TRANSFER TIMES v. The problem may be considered as dynamic handling devices scheduling problem, where tasks service ready times are known after the beginning of the planning interval, or as static problem, where all tasks are already known when the scheduling plan is determined v. Here, only static problem (SHDAP) is studied

Mathematical formulation v. There are I handling devices and N barges (I < N) v. Each barge has its own time of appearance Ak v. Each handling device (i) has known productivity pik, dependant on the barge to be served v. Since barge has capacity of qk, task (k) completion time is, Cik=qk/pik. v. Transfer time tijk of handling device (i), between nodes (j) and (k) depends on the distance djk, travel speed Vi, and on the handling device preparation time Di after handling of barge (j), as well as on the preparation time Ei before handling barge (k)

Plan alokacije pretovarnih postrojenja za istovar šljunka iz barži. . . Trodimenzioni problem dodeljivanja Vreme transfera opsluge Vreme dolaska

Mathematical formulation … Second formulation v. Based on analogy with the static berth allocation problem transfer handling arrival time

Solution approach Idea 1. Classifying nodes into clusters whose number is equal to the number of handling devices 2. Assigning each of handling devices to those clusters 3. Sequencing nodes (barges) in each cluster in non decreasing order of its service times, and 4. Improving the obtained solution

Heuristic algorithm - CLASORD HEURISTICS CLUSTERING PHASE ORDERING AND ASSIGNMENT PHASE 1. For all nodes assigned to a cluster, calculate service time τijk, when nodes are served by handling devices (i): τijk=tijk+Cik i Starting from depot (j=0) find closest nodes (k) so that is satisfied ii iii 2. 3. 4. τijk=min(τi 01, τi 02, . . . , τi 0 k) Set j=k, and find next closest node to j Repeat ii) until all nodes in the cluster are ordered, denoting order of nodes in the cluster z, when served by device i, as θzi Calculate the total waiting time T(θzi) of all barges in the cluster Repeat Steps 1 and 2 for all of I clusters, and all handling devices Assign handling devices to clusters by solving the two dimensional assignment problem Keep record of the solution SOLUTION IMPROVEMENT PHASE

Numerical Example … Ø three handling devices (I=3) and seven nodes (barges) (N=7) Ø same speed, which is 5 km/h Ø unloading productivities pik are 100 t / h, 150 t / h and 200 t / h Ø nodes have equal demand of 1000 t

Numerical Example … Ø ordering and assignment phase Cluster 1 served by handling device 1 θ 11= θ 12= θ 13 = {2, 1, 3} Similarly θ 21= θ 22= θ 23={4, 5} θ 31= θ 32= θ 33= {6, 7}

Numerical Example … Waiting times of barges T(θzi) Handling device Clusters 1 2 3 1 124 46 58 2 104 36 48 3 94 31 43

Conclusions & and future research vproposed algorithm is very simple for application, and gives good solutions in a very short time, which suggest a possibility for practical use vit is necessary to continue with its implementation to additional examples, particularly to larger problems (for example 20 nodes) vheuristic performances determination vadoption to real system requirements, particularly in the context of node priorities vdynamic problem solving

Plana rada kojim se minimizira ukupan broj pretovarnih sredstava koje treba angažovati Realizacija pretovarnih zadataka sredstvima cikličnog dejstvapodrazumeva realizaciju jednog ili više ciklusa između mesta u kome postoji zahtev za robom i mesta gde se roba nalazi. Ukoliko postoji više zadataka ovog tipa, za čiju realizaciju je na raspolaganju veći broj pretovarnih sredstava, postavlja se i logično pitanje koji je to minimalni broj sredstava sa kojim je u nekom unapred zadatom vremenu TR moguće realizovati sve zahteve koji su u sistemu prisutni u trenutku t=0? .

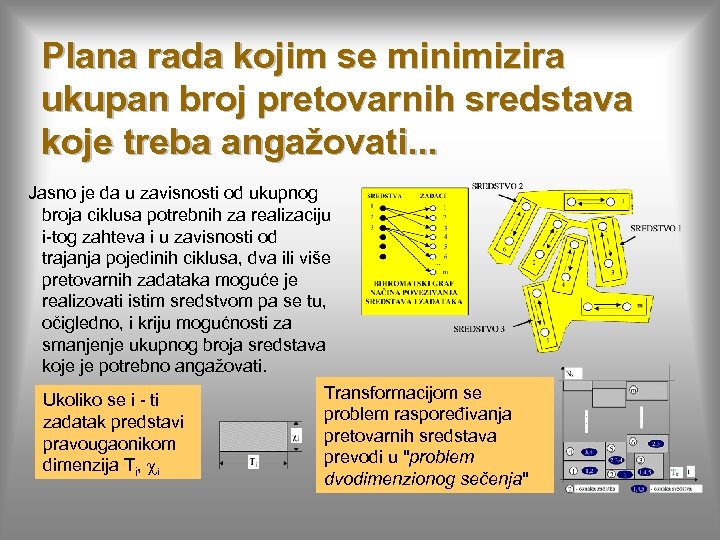Plana rada kojim se minimizira ukupan broj pretovarnih sredstava koje treba angažovati. . . Jasno je da u zavisnosti od ukupnog broja ciklusa potrebnih za realizaciju i-tog zahteva i u zavisnosti od trajanja pojedinih ciklusa, dva ili više pretovarnih zadataka moguće je realizovati istim sredstvom pa se tu, očigledno, i kriju mogućnosti za smanjenje ukupnog broja sredstava koje je potrebno angažovati. Transformacijom se Ukoliko se i - ti problem raspoređivanja zadatak predstavi pretovarnih sredstava pravougaonikom prevodi u "problem dimenzija Ti, i dvodimenzionog sečenja"

Hvala na pažnji !