Operations Management Inventory Management Chapter 12 — Part

Operations Management Inventory Management Chapter 12 - Part I 1

Outline ¨ Functions of Inventory. ¨ ABC Analysis. ¨ Inventory Costs. ¨ Inventory Models for Independent Demand. ¨ Economic Order Quantity (EOQ) Model. ¨ Production Order Quantity (POQ) Model. ¨ Quantity Discount Model. ¨ Probabilistic Models with Varying Demand. 2

Types of Inventory ¨Raw materials. ¨Work-in-progress. ¨Maintenance/repair/operating (MRO) supply. ¨Finished goods. 3

The Functions of Inventory ¨ To ”decouple” or separate various parts of the production process. ¨ To smooth production (link supply and demand). ¨ To provide goods for customers (quick response). ¨ To take advantage of quantity discounts. ¨ Buy more to get a reduced price. ¨ To hedge against inflation and upward price changes (speculation). 4

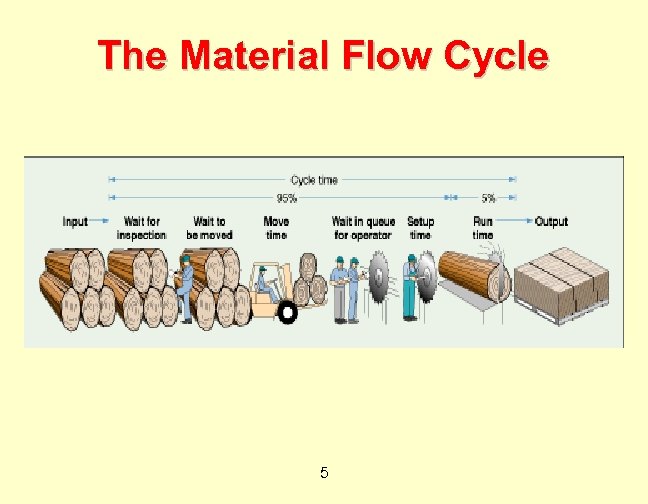The Material Flow Cycle 5

Disadvantages of Inventory ¨ High cost - $$$$$ ¨ Money tied up in inventory could be better used elsewhere in the organization. ¨ Difficult to control. ¨ Inventories occur in many places. ¨ Hides production problems. ¨ Large inventories may overcome poor quality production or poor quality materials. 6

ABC Analysis ¨ Divide inventory into 3 classes based on annual $ volume. ¨ Annual $ volume = Annual demand x Unit cost. A class - Most important. 15 -20% of products. 60 -80% of value. B class -Less important. 20 -40% of products. 15 -30% of value. C class - Least important. 50 -60% of products. 7 5 -10% of value.

ABC Analysis ¨ Sort products from largest to smallest annual $ volume. ¨ Divide into A, B and C classes. ¨ Focus on A products. ¨ Develop class A suppliers more. ¨ Give tighter physical control of A items. ¨ Forecast A items more carefully. ¨ Consider B products only after A products. 8

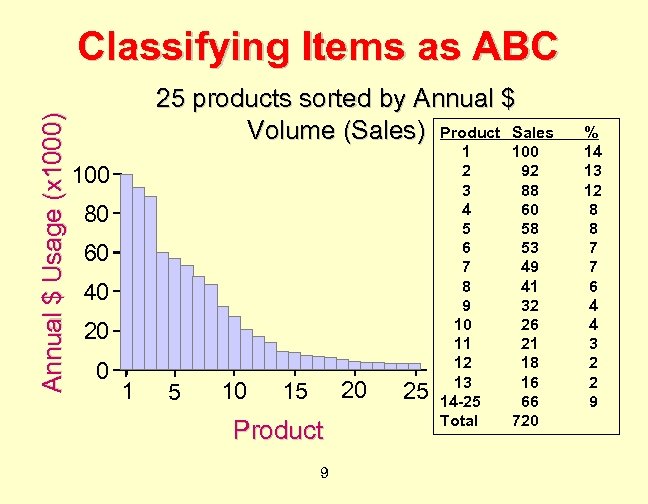Annual $ Usage (x 1000) Classifying Items as ABC 25 products sorted by Annual $ Volume (Sales) Product Sales 100 80 60 40 20 0 1 5 10 20 15 Product 9 25 1 2 3 4 5 6 7 8 9 10 11 12 13 14 -25 Total 100 92 88 60 58 53 49 41 32 26 21 18 16 66 720 % 14 13 12 8 8 7 7 6 4 4 3 2 2 9

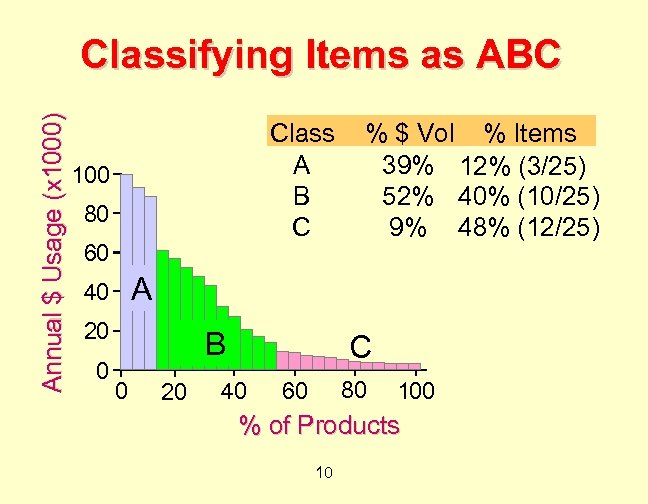Annual $ Usage (x 1000) Classifying Items as ABC Class A B C 100 80 60 A 40 20 0 % $ Vol % Items 39% 12% (3/25) 52% 40% (10/25) 9% 48% (12/25) B 0 20 C 40 80 60 100 % of Products 10

Inventory Accuracy ¨ Inventory accuracy importance: ¨ To determine when and how much to order. ¨ To achieve high level of service. ¨ Information system tracks inventory, but… ¨ Not all items sold are entered (scanned) properly. ¨ Some items disappear without being sold (theft, defective, damaged, etc. ) 11

Inventory Counting ¨ Count products to verify inventory records. ¨ Shut down facility and count everything at one time (once per year). ¨ Cycle counting: count items continuously (count some each week). ¨ Count A items most frequently (for example, once a month). ¨ Count B items less frequently (twice a year). ¨ Count C items least frequently (once a 12 year).

Inventory for Services ¨ Can be large $. ¨ “Shrinkage” (theft) is a problem. ¨ Often over 3%! ¨ Good personnel selection, training, and discipline is key. ¨ Establish tight control of shipments entering and leaving the facility. ¨ Enforce procedures for documenting product movement. ¨ Information systems can monitor inventory levels and help ensure accuracy. 13

Inventory Costs ¨ Holding costs - Associated with holding or “carrying” inventory over time. ¨ Ordering costs - Associated with costs of placing order and receiving goods. ¨ Setup costs - Cost to prepare a machine or process for manufacturing an order. ¨ Stockout costs - Cost of not making 14

Holding Costs ¨ Investment costs (borrowing, interest). ¨ Insurance. ¨ Taxes. ¨ Storage and handling. ¨ Extra staffing. ¨ Pilferage, damage, spoilage, scrap. ¨ Obsolescence. 15

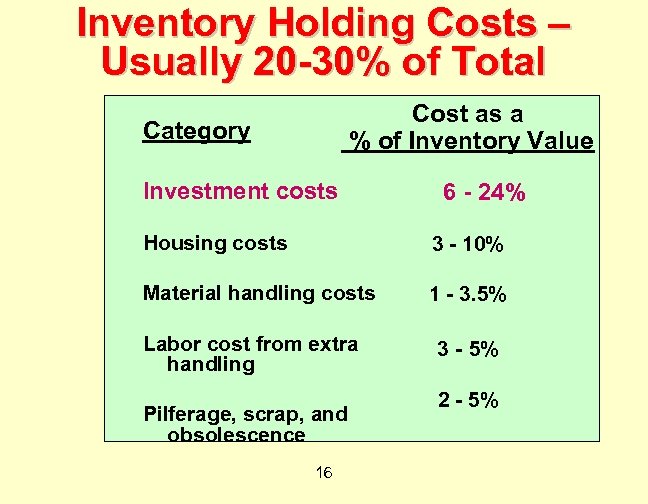Inventory Holding Costs – Usually 20 -30% of Total Cost as a % of Inventory Value Category Investment costs 6 - 24% Housing costs 3 - 10% Material handling costs 1 - 3. 5% Labor cost from extra handling Pilferage, scrap, and obsolescence 16 3 - 5% 2 - 5%

Ordering Costs To order and receive product: ¨ Supplies. ¨ Forms. ¨ Order processing. ¨ Clerical support. ¨ etc. 17

Setup Costs To change equipment and setup for new product: ¨ Clean-up costs. ¨ Re-tooling costs. ¨ Adjustment costs. ¨ etc. 18

Stockout Costs For not making a sale and for lost future sales: - Customer may wait for a backorder, or - Cancel order (and acquire product elsewhere). ¨ Backorder costs: expediting, special orders, rush shipments, etc. ¨ Lost current sale cost. 19 ¨ Lost future sales (hard to estimate).

Inventory Questions ¨ How much to order (each time)? ¨ 100 units, 50 units, 23. 624 units, etc. ¨ When to order? ¨ Every 3 days, every week, every month, etc. ¨ When only 5 items are left, when only 10 items are left, when only 20 items are left, etc. ¨ Many different models can be used, depending on nature of products and demand. 20

Independent vs. Dependent Demand ¨ Independent demand - Demand for item is independent of demand for any other item. ¨ Dependent demand - Demand for item depends upon the demand for some other item. ¨ Example: Demand for car engines depends on demand for new cars. ¨ We will consider only independent 21 demand.

Inventory Models ¨ Fixed order-quantity models. ¨ 1. Economic order quantity (EOQ). ¨ 2. Production order quantity (POQ). ¨ 3. Quantity discount. ¨ Probabilistic models. ¨ Fixed order-period models. 22 How much and when to order?

How Much and When to Order? ¨ Given a fixed annual demand for a product. ¨ With many small orders: ¨ Amount on hand is always small, so inventory is small. ¨ Frequent orders means cost of ordering is large. ¨ With few large orders: ¨ Amount on hand may be large (when order arrives), so inventory may be large. ¨ 23 Infrequent orders mean cost of ordering is

EOQ – Economic Order Quanitity Models ¨ How much to order (each time)? ¨ Order size is a constant = Q ¨ Q is selected to minimize total cost. ¨ When to order? ¨ Order when amount remaining = ROP 24

EOQ Assumptions ¨ Known and constant demand. ¨ Known and constant lead time. ¨ Instantaneous receipt of material. ¨ No quantity discounts. ¨ Only order cost and holding cost. ¨ No stockouts. 25

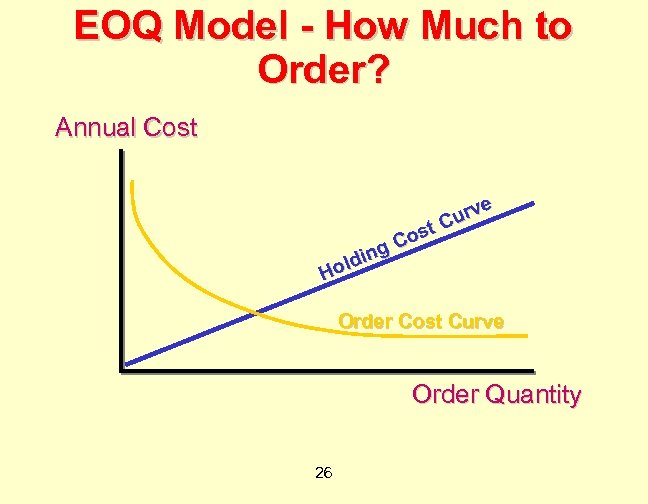EOQ Model - How Much to Order? Annual Cost g ldin Ho e urv C ost C Order Cost Curve Order Quantity 26

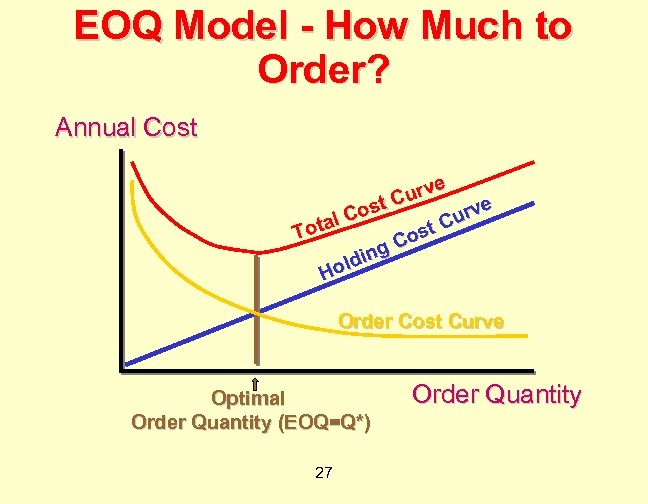EOQ Model - How Much to Order? Annual Cost e urv C e ost urv l. C a C Tot ost C ing old H Order Cost Curve Optimal Order Quantity (EOQ=Q*) 27 Order Quantity

Why Holding Costs Increase ¨ For fixed annual demand, larger order quantities means: ¨ Larger inventory (larger amount ordered each time). ¨ Larger inventory holding cost. ¨ Example: Annual demand = 1200 units ¨ Order 600 each time. ¨ ¨ Maximum inventory = 600 Order 50 each time. ¨ Maximum inventory = 50 28

Why Order Costs Decrease ¨ For fixed annual demand, larger order quantities means: ¨ Fewer orders per year. ¨ Smaller order cost per year. ¨ Example: Annual demand = 1200 units ¨ Order 600 each time. ¨ ¨ 1200/600 = 2 orders per year. Order 50 each time. ¨ 1200/50 = 24 orders per year. 29

Deriving an EOQ ¨ Develop an expression for total costs. ¨ Total cost = order cost + holding cost ¨ Find order quantity that gives minimum total cost (use calculus). ¨ Minimum ¨ Slope is when slope is flat. = Derivative. ¨ Set derivative of total cost equal to 0 and solve for best order quantity. 30

EOQ Model Equations D = Annual demand (relatively constant) S = Order cost per order H = Holding (carrying) cost per unit per year d = Demand rate (units per day, units per week, etc. ) L = Lead time (constant) (in days, weeks, hours, etc. ) Give n Determine: Q = Order size (number of items per order) D Expected Number of Orders per year =N= Q D Order Cost per year S = Q Holding Cost per year = (average inventory level) H 31

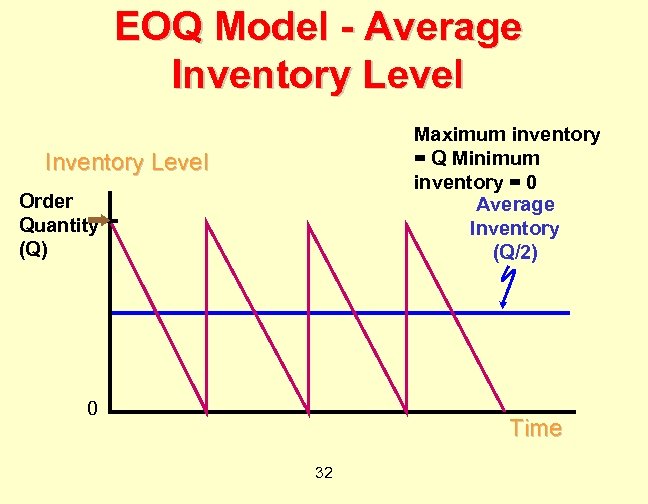EOQ Model - Average Inventory Level Maximum inventory = Q Minimum inventory = 0 Average Inventory (Q/2) Inventory Level Order Quantity (Q) 0 Time 32

EOQ Model Equations D = Annual demand (relatively constant) S = Order cost per order H = Holding (carrying) cost per unit per year d = Demand rate (units per day, units per week, etc. ) L = Lead time (constant) (in days, weeks, hours, etc. ) Give n Determine: Q = Order size (number of items per order) D Expected Number of Orders per year =N= Q D Order Cost per year S = Q Q H Holding Cost per = (average inventory level) 2 year H= 33

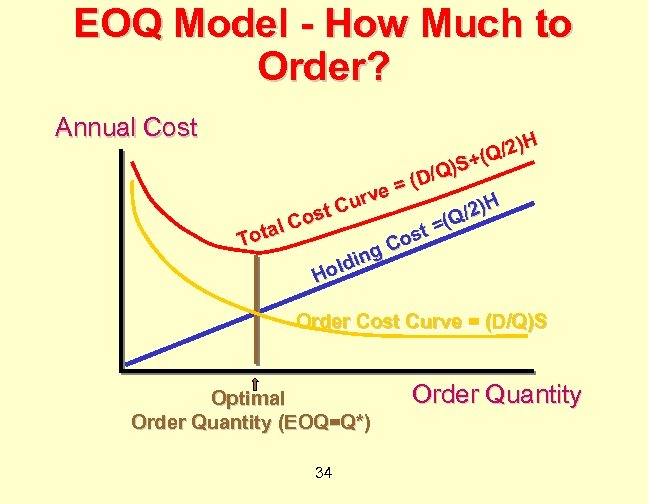EOQ Model - How Much to Order? Annual Cost )H (Q/2 + Q)S / = (D e urv /2)H st C o Q t =( tal C s To Co g din l Ho Order Cost Curve = (D/Q)S Optimal Order Quantity (EOQ=Q*) 34 Order Quantity

EOQ Total Cost Optimization = Total Cost D Q S+ H Q 2 Take derivative of total cost with respect to Q and set equal to zero: D 1 S+ H=0 2 Q 2 Solve for Q to get optimal order size: 2 ×D ×S EOQ = Q* = H 35

EOQ Model Equations D = Annual demand S = Order cost per order H = Holding (carrying) cost 2 ×D ×S H D Expected Number of Orders N = = Q* Optimal Order Quantity = Q* = Expected Time Between Orders= =T 36 Working Days / Year N

EOQ Model - When to order? D = Annual demand (relatively constant) Give n d = Demand per day L = Lead time in days Determine: ROP = reorder point (number of pieces or items remaining when order is to be placed) D Suppose demand is 10 per = d Working Days / Year ROP = d × L day and lead time is (always) 4 days. When should you order? When 40 are left! 37

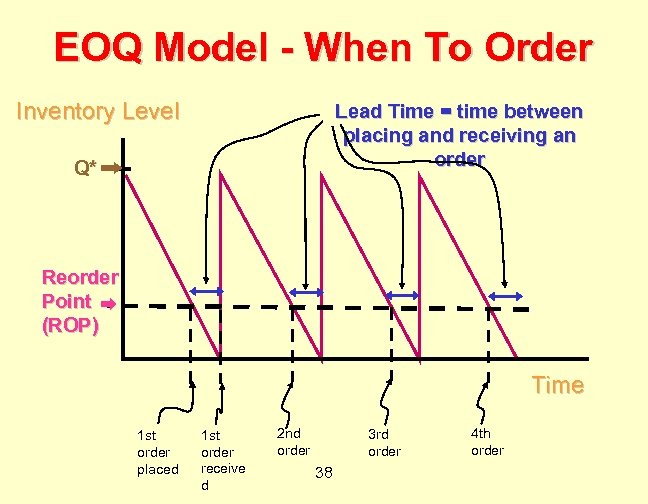EOQ Model - When To Order Inventory Level Lead Time = time between placing and receiving an order Q* Reorder Point (ROP) Time 1 st order placed 1 st order receive d 2 nd order 3 rd order 38 4 th order

EOQ Example Demand = 1200/year Order cost = $50/order Holding cost = $5 per year per item 260 working days per year = Q* = 2 × 1200 × 50 154. 92 units/order; so order 155 each time 5 1200/year Expected Number of Orders = N = = 155 7. 74/year 260 Expected Time Between Orders days/year =T= = 33. 6 days 7. 74/year 1200 155 Total Cost = 50 5 = 387. 10 + 387. 50 = 2 $774. 60/year 155 + 39

EOQ is Robust Demand = 1200/year Order cost = $50/order Holding cost = $5 per year per item 260 working days per year 1200 Q Total Cost = 5 50 + 2 Q Q = 155 units/order TC = $774. 60/year Q* = 154. 92 units/order TC = $774. 60/year = 387. 3 Suppose we must order in multiples of 20: Q = 140 units/order TC = $778. 57/year (+0. 5 Q = 160 units/order TC = $775. 00/year (+0. 0 Cost is nearly optimal! 40

EOQ is Robust Demand = 1200/year Order cost = $50/order Holding cost = $5 per year per item 260 working days per year Q = 155 units/order Q* = 154. 92 units/order 387. 30 + 387. 30 1200 Q Total Cost = 5 50 + 2 Q TC = $774. 60/year = Suppose we wish to order 6 times per year (every 2 months): Q = 1200/6 = 200 units/order above Q*) (200/order is 29% 41 TC = $800. 00/year = 300. 00 + 500. 00

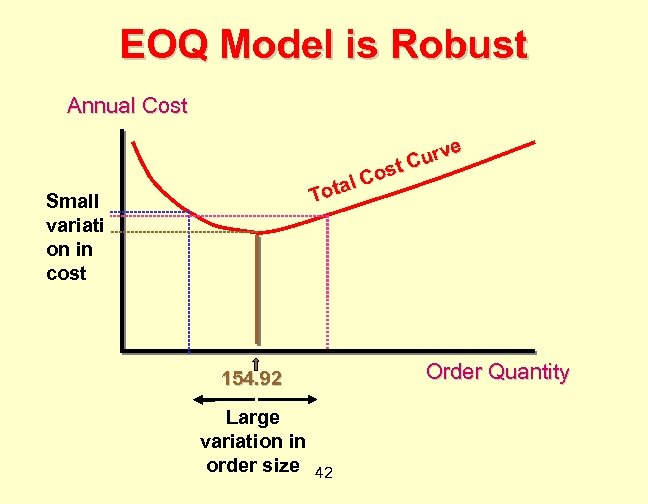EOQ Model is Robust Annual Cost e urv C ost C otal T Small variati on in cost Order Quantity 154. 92 Large variation in order size 42

Robustness ¨ EOQ amount can be adjusted to facilitate business practices. ¨ If order size is reasonably near optimal (+ or - 20%), then cost will be very near optimal (within a few percent). ¨ If parameters (order cost, holding cost, demand) are not known with certainty, then EOQ is still very useful. 43

EOQ Model - When to order? Demand = 1200/year Order cost = $50/order Holding cost = $5 per year per item 260 working days per year Lead time = 5 days 1200/year = 4. 615/day d= 260 days/year ROP = 4. 615 units/day 5 days = 23. 07 units -> Place an order whenever inventory falls to (or below) 44