ОПЕРАЦИИ НАД ГРАФАМИ И СПОСОБЫ ПРЕДСТАВЛЕНИЯ ГРАФОВ 1

ОПЕРАЦИИ НАД ГРАФАМИ И СПОСОБЫ ПРЕДСТАВЛЕНИЯ ГРАФОВ 1. Подграфы. 2. Операции над графами. 3. Способы представления графов.

Вопрос 1. Подграфы О. 1. 1. Граф Gʹ(Vʹ, Еʹ) называется подграфом графа G(V, Е), если Vʹ V и Еʹ Е. О. 1. 2. Если Vʹ = V, то граф Gʹ(Vʹ, Еʹ) называется остовным подграфом графа G(V, Е). О. 1. 3. Если каждое ребро {u, v} графа G такое, что u, v Vʹ, присутствует и в графе Gʹ, то подграф Gʹ называется подграфом, индуцированным (порожденным) множеством вершин Vʹ.

Пример 1. Дан граф G. Тогда: • G 1 – остовной подграфа G; • G 2 – подграфа G, индуцированный множеством вершин{u 1, u 2, u 3}; • G 3 – подграф, не являющийся остовным или индуцированным; • G 4 – не является подграфом графа G.

Вопрос 2. Операции над графами Одноместные (унарные) операции Пусть дан граф G(V, Е) с множеством вершин V и множеством ребер Е. 1. Операция удаления вершины u из графа G(V, Е) состоит в образовании графа G 1(V 1, Е 1) такого, что V 1 = V{u}, а множество Е 1 получается из множества Е удалением всех ребер, инцидентных вершине u. Обозначение: G 1 = G ‒ u.

2. Операция добавления вершины u V в граф G(V, Е) состоит в образовании графа G 1(V 1, Е 1) такого, что V 1 = V {u} и Е 1 = Е. Обозначение: G 1 = G + u. 3. Операция удаления ребра е из графа G(V, Е) состоит в образовании графа G 1(V 1, Е 1) такого, что V 1 = V и Е 1 = Е{е}. Обозначение: G 1 = G ‒ е. 4. Операция добавления ребра е Е, концы которого принадлежат графу G(V, Е), состоит в образовании графа G 1(V 1, Е 1) такого, что V 1 = V и Е 1 = Е {е}. Обозначение: G 1 = G + е.

5. Операция отождествления вершин u и v в графе G(V, Е) состоит в образовании графа G 1(V 1, Е 1), получающегося путем удаления из графа G вершин u и v, добавления новой вершины uʹ и соединения этой вершины ребрами со всеми вершинами, смежными с вершинами u и v. В случае, когда вершины u и v соединены ребром операцию отождествления вершин u и v называют стягиванием ребра {u, v}.

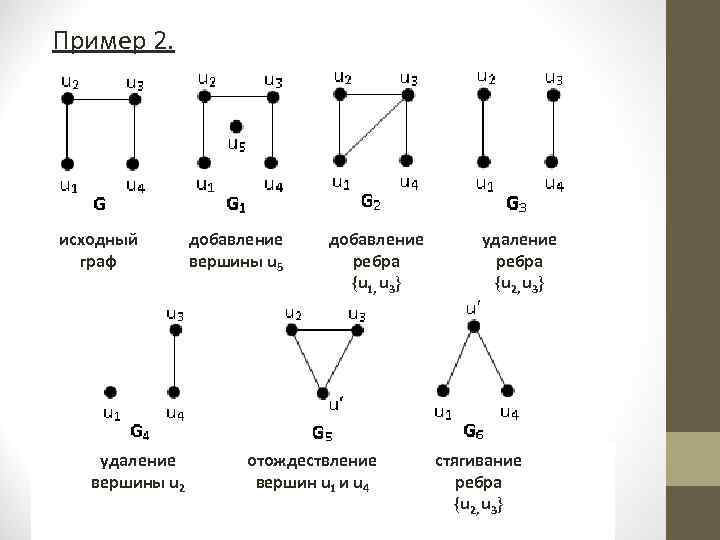
Пример 2. исходный граф удаление вершины u 2 добавление вершины u 5 добавление ребра {u 1, u 3} отождествление вершин u 1 и u 4 удаление ребра {u 2, u 3} стягивание ребра {u 2, u 3}

О. 2. 1. Граф называется дополнением графа G(V, Е), если множества их вершин совпадают, т. е. а вершины в смежны тогда и только тогда, когда они не смежны в G. Графы называются дополнительными друг к другу. Другими словами, чтобы получить дополнение графа G, следует удалить из G все ребра и соединить ребрами те вершины, которые в G не были смежными.

Двуместные (бинарные) операции Пусть даны два графа G 1(V 1, Е 1) и G 2(V 2, Е 2). О. 2. 2. Объединением графов G 1 и G 2 называется граф G = G 1 G 2 с множеством вершин V = V 1 V 2 и множеством ребер Е = Е 1 Е 2. Объединение графов G = G 1 G 2 называется дизъюнктивным, если у графов G 1 и G 2 нет общих вершин, т. е. V 1 V 2 = . О. 2. 3. Пересечением графов G 1 и G 2 называется граф G = G 1 G 2 с множеством вершин V = V 1 V 2 и множеством ребер Е = Е 1 Е 2.

О. 2. 4. Кольцевой суммой графов G 1 и G 2 называется граф G = G 1 G 2 с множеством вершин V = V 1 V 2 и множеством ребер Е = (Е 1 Е 2)( Е 1 Е 2), т. е. это граф, порожденный на множестве ребер, присутствующих либо в G 1, либо в G 2, но не принадлежащих их пересечению G 1 G 2.

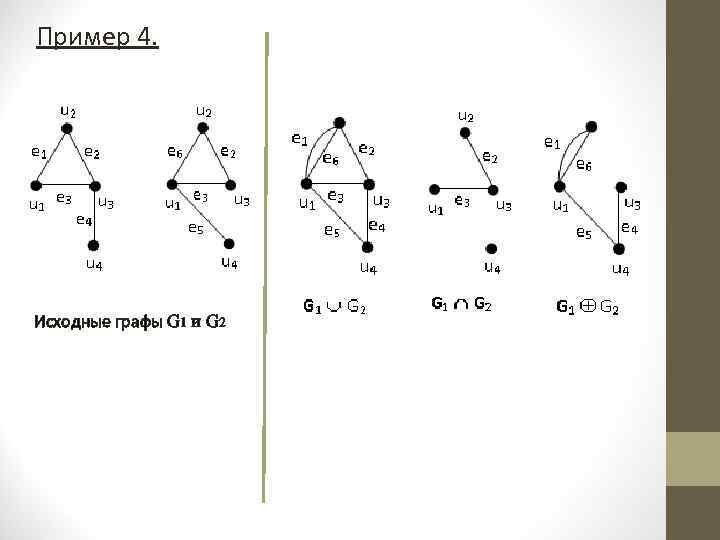
Пример 4. Исходные графы G 1 и G 2

О. 2. 5. Соединением графов G 1 и G 2 называется граф G = G 1 + G 2 с множеством вершин V = V 1 V 2 и множеством ребер е, состоящим из всех ребер, принадлежащих графам G 1 и G 2, и всех ребер, соединяющих каждую вершину графа G 1 с каждой вершиной графа G 2, т. е. Е = Е 1 Е 2 {е = {v 1, v 2}| v 1 V 1 и v 2 V 2}.

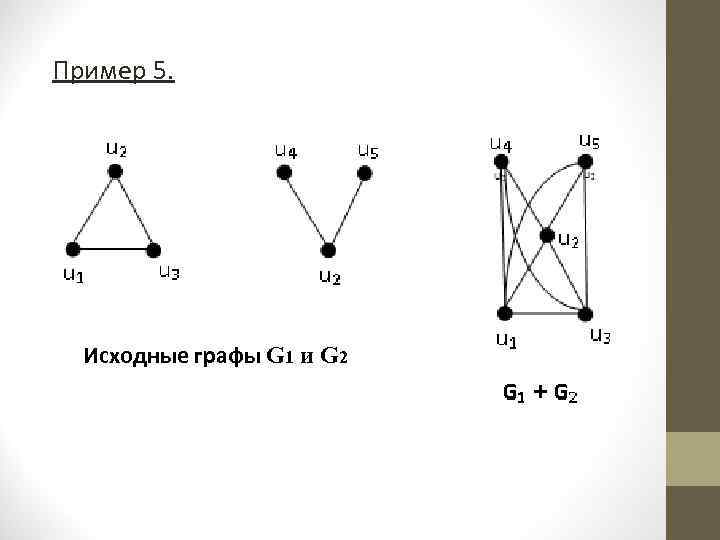
Пример 5. Исходные графы G 1 и G 2

Вопрос 3. Способы представления графов Представление графов матрицами Пусть дан граф (орграф) G(V, Е) с множеством вершин V = {u 1, u 2, …, un} и множеством ребер (дуг) Е = {е 1, е 2, …, еm}. О. 3. 1. Матрицей смежности графа (орграфа) G называется квадратная матрица n-го порядка А = (аij)n, n, у которой элемент аij равен числу ребер (дуг), соединяющих вершины ui и uj (идущих из ui в uj).

Если граф (орграф) не содержит кратных ребер (дуг), то Если граф не имеет петель, то все диагональные элементы матрицы смежности равны 0. Замечание Матрица смежности неориентированного графа является симметричной, а матрица смежности ориентированного графа симметричной, в общем случае не является.

Пример 6.

Т. 3. 1. Графы G 1 и G 2 изоморфны тогда и только тогда, когда их матрицы смежности получаются друг из друга одновременными перестановками строк и столбцов (т. е. одновременно с перестановкой i-той и j-той строк переставляются iтый и j-тый столбцы). Согласно т. 3. 1 по матрице смежности граф восстанавливается однозначно с точностью до изоморфизма.

О. 3. 2. Матрицей инцидентности (инциденций) неориентированного графа G называется матрица В = (bij)n, m размера n m, где n – число вершин, а m – число ребер графа G, определяемая следующим образом: Пример 7.

Свойства матрицы инцидентности неориентированного графа 1. В графе без петель каждый столбец матрицы имеет в точности две единицы, соответствующие паре вершин ребра. 2. Если в графе имеются петли, то в столбцах, соответствующих петлям, имеется по одной единице, а в остальных – по две.

О. 3. 3. Матрицей инцидентности (инциденций) ориентированного графа G называется матрица В = (bij)n, m размера n m, где n – число вершин, а m – число дуг орграфа G, определяемая следующим образом:

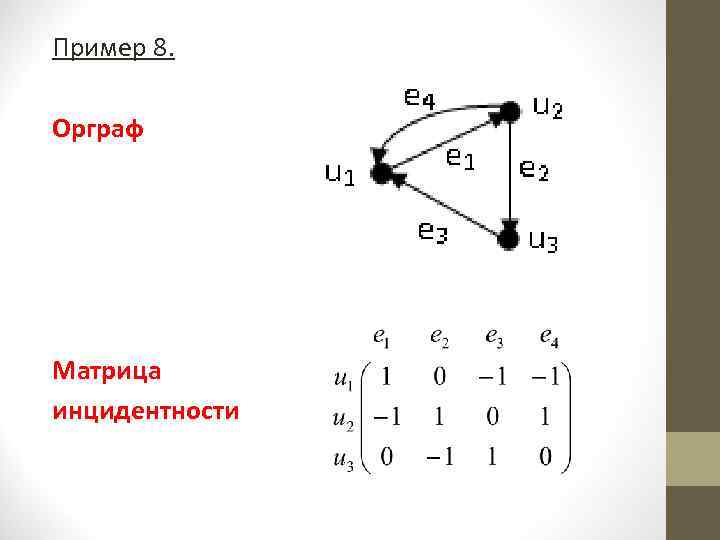
Пример 8. Орграф Матрица инцидентности

Ориентированный граф, как правило, петель не содержит. Его матрица инцидентности имеет в каждом столбце +1 и 1, которые отвечают началу и концу каждого ребра. Иногда матрицу инцидентности для орграфа задают иначе:

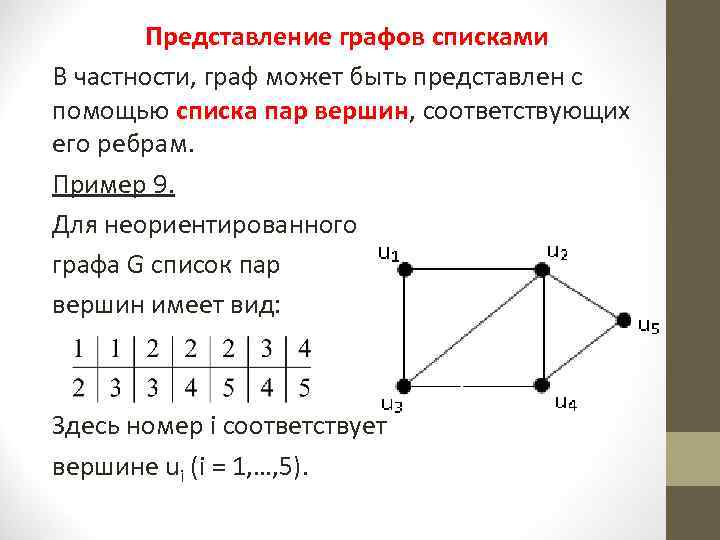
Представление графов списками В частности, граф может быть представлен с помощью списка пар вершин, соответствующих его ребрам. Пример 9. Для неориентированного графа G список пар вершин имеет вид: Здесь номер i соответствует вершине ui (i = 1, …, 5).

Во многих случаях лучшим способом описания графов является структура данных, называемая списком смежности. Эта структура для каждой вершины, помеченной признаком «начало» , содержит список вершин, смежных с данной вершиной. Каждый список вершин заканчивается признаком «конец» . Размерность такой структуры равна m + n для ориентированного графа и n + 2 m – для неориентированного графа.

Пример 10.